Introduction to quantum mechanics

A side portrait of Planck as a young adult, c. 1878

Hot metalwork. The yellow-orange glow is the visible part of the thermal radiation emitted due to the high temperature. Everything else in the picture is glowing with thermal radiation as well, but less brightly and at longer wavelengths than the human eye can detect. A far-infrared camera can observe this radiation.

Thermal radiation is electromagnetic radiation emitted from the surface of an object due to the object's internal energy. If an object is heated sufficiently, it starts to emit light at the red end of the spectrum, as it becomes red hot.

Heating it further causes the color to change from red to yellow, white, and blue, as it emits light at increasingly shorter wavelengths (higher frequencies). A perfect emitter is also a perfect absorber: when it is cold, such an object looks perfectly black, because it absorbs all the light that falls on it and emits none. Consequently, an ideal thermal emitter is known as a black body, and the radiation it emits is called black-body radiation.

Predictions of the amount of thermal radiation of different frequencies emitted by a body. Correct values predicted by Planck's law (green) contrasted against the classical values of Rayleigh-Jeans law (red) and Wien approximation (blue).

By the late 19th century, thermal radiation had been fairly well characterized experimentally.[note 1] However, classical physics led to the Rayleigh–Jeans law, which, as shown in the figure, agrees with experimental results well at low frequencies, but strongly disagrees at high frequencies. Physicists searched for a single theory that explained all the experimental results.

The first model that was able to explain the full spectrum of thermal radiation was put forward by Max Planck in 1900.[6] He proposed a mathematical model in which the thermal radiation was in equilibrium with a set of harmonic oscillators. To reproduce the experimental results, he had to assume that each oscillator emitted an integer number of units of energy at its single characteristic frequency, rather than being able to emit any arbitrary amount of energy. In other words, the energy emitted by an oscillator was quantized.[note 2] The quantum of energy for each oscillator, according to Planck, was proportional to the frequency of the oscillator; the constant of proportionality is now known as the Planck constant. The Planck constant, usually written as h, has the value of 6.63×10⁻³⁴ J s. So, the energy E of an oscillator of frequency f is given by

${\displaystyle E=nhf,\quad {\text{where}}\quad n=1,2,3,\ldots }$[7]

To change the color of such a radiating body, it is necessary to change its temperature. Planck's law explains why: increasing the temperature of a body allows it to emit more energy overall, and means that a larger proportion of the energy is towards the violet end of the spectrum.

Planck's law was the first quantum theory in physics, and Planck won the Nobel Prize in 1918 "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta".[8] At the time, however, Planck's view was that quantization was purely a heuristic mathematical construct, rather than (as is now believed) a fundamental change in our understanding of the world.[9]

Albert Einstein c. 1905

In 1905, Albert Einstein took an extra step. He suggested that quantization was not just a mathematical construct, but that the energy in a beam of light actually occurs in individual packets, which are now called photons.[10] The energy of a single photon of light of frequency ${\displaystyle f}$ is given by the frequency multiplied by Planck's constant ${\displaystyle h}$ (an extremely tiny positive number):

${\displaystyle E=hf}$

For centuries, scientists had debated between two possible theories of light: was it a wave or did it instead comprise a stream of tiny particles? By the 19th century, the debate was generally considered to have been settled in favor of the wave theory, as it was able to explain observed effects such as refraction, diffraction, interference, and polarization.[11] James Clerk Maxwell had shown that electricity, magnetism, and light are all manifestations of the same phenomenon: the electromagnetic field. Maxwell's equations, which are the complete set of laws of classical electromagnetism, describe light as waves: a combination of oscillating electric and magnetic fields. Because of the preponderance of evidence in favor of the wave theory, Einstein's ideas were met initially with great skepticism. Eventually, however, the photon model became favored. One of the most significant pieces of evidence in its favor was its ability to explain several puzzling properties of the photoelectric effect, described in the following section. Nonetheless, the wave analogy remained indispensable for helping to understand other characteristics of light: diffraction, refraction, and interference.

The photoelectric effect

Light is shone upon the surface from the left. If the light frequency is high enough, i.e. if it delivers sufficient energy, negatively charged electrons are ejected from the metal.

Main article: Photoelectric effect

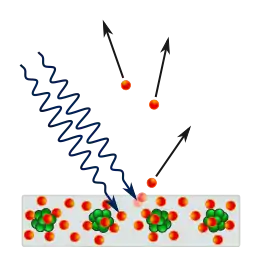
In 1887, Heinrich Hertz observed that when light with sufficient frequency hits a metallic surface, the surface emits electrons.[12] In 1902, Philipp Lenard discovered that the maximum possible energy of an ejected electron is related to the frequency of the light, not to its intensity: if the frequency is too low, no electrons are ejected regardless of the intensity. Strong beams of light toward the red end of the spectrum might produce no electrical potential at all, while weak beams of light toward the violet end of the spectrum would produce higher and higher voltages. The lowest frequency of light that can cause electrons to be emitted, called the threshold frequency, is different for different metals. This observation is at odds with classical electromagnetism, which predicts that the electron's energy should be proportional to the intensity of the incident radiation.[13]^: 24 So when physicists first discovered devices exhibiting the photoelectric effect, they initially expected that a higher intensity of light would produce a higher voltage from the photoelectric device.

Einstein explained the effect by postulating that a beam of light is a stream of particles ("photons") and that, if the beam is of frequency f, then each photon has an energy equal to hf.[12] An electron is likely to be struck only by a single photon, which imparts at most an energy hf to the electron.[12] Therefore, the intensity of the beam has no effect[note 3] and only its frequency determines the maximum energy that can be imparted to the electron.[12]

To explain the threshold effect, Einstein argued that it takes a certain amount of energy, called the work function and denoted by φ, to remove an electron from the metal.[12] This amount of energy is different for each metal. If the energy of the photon is less than the work function, then it does not carry sufficient energy to remove the electron from the metal. The threshold frequency, f₀, is the frequency of a photon whose energy is equal to the work function:

${\displaystyle \varphi =hf_{0}.}$

If f is greater than f₀, the energy hf is enough to remove an electron. The ejected electron has a kinetic energy, E_K, which is, at most, equal to the photon's energy minus the energy needed to dislodge the electron from the metal:

${\displaystyle E_{K}=hf-\varphi =h(f-f_{0}).}$

Einstein's description of light as being composed of particles extended Planck's notion of quantized energy, which is that a single photon of a given frequency, f, delivers an invariant amount of energy, hf. In other words, individual photons can deliver more or less energy, but only depending on their frequencies. In nature, single photons are rarely encountered. The Sun and emission sources available in the 19th century emit vast numbers of photons every second, and so the importance of the energy carried by each photon was not obvious. Einstein's idea that the energy contained in individual units of light depends on their frequency made it possible to explain experimental results that had seemed counterintuitive. However, although the photon is a particle, it was still being described as having the wave-like property of frequency. Effectively, the account of light as a particle is insufficient, and its wave-like nature is still required.[14][note 4]

By the dawn of the 20th century, the evidence required a model of the atom with a diffuse cloud of negatively charged electrons surrounding a small, dense, positively charged nucleus. These properties suggested a model in which electrons circle the nucleus like planets orbiting a star.[note 5] However, it was also known that the atom in this model would be unstable: according to classical theory, orbiting electrons are undergoing centripetal acceleration, and should therefore give off electromagnetic radiation, the loss of energy also causing them to spiral toward the nucleus, colliding with it in a fraction of a second.

A second, related puzzle was the emission spectrum of atoms. When a gas is heated, it gives off light only at discrete frequencies. For example, the visible light given off by hydrogen consists of four different colors, as shown in the picture below. The intensity of the light at different frequencies is also different. By contrast, white light consists of a continuous emission across the whole range of visible frequencies. By the end of the nineteenth century, a simple rule known as Balmer's formula showed how the frequencies of the different lines related to each other, though without explaining why this was, or making any prediction about the intensities. The formula also predicted some additional spectral lines in ultraviolet and infrared light that had not been observed at the time. These lines were later observed experimentally, raising confidence in the value of the formula.

Emission spectrum of hydrogen. When excited, hydrogen gas gives off light in four distinct colors (spectral lines) in the visible spectrum, as well as a number of lines in the infrared and ultraviolet.

The Bohr model of the atom, showing an electron transitioning from one orbit to another by emitting a photon

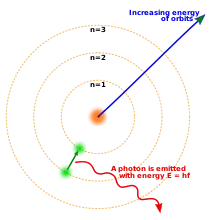
In 1913 Niels Bohr proposed a new model of the atom that included quantized electron orbits: electrons still orbit the nucleus much as planets orbit around the sun, but they are permitted to inhabit only certain orbits, not to orbit at any arbitrary distance.[19] When an atom emitted (or absorbed) energy, the electron did not move in a continuous trajectory from one orbit around the nucleus to another, as might be expected classically. Instead, the electron would jump instantaneously from one orbit to another, giving off the emitted light in the form of a photon.[20] The possible energies of photons given off by each element were determined by the differences in energy between the orbits, and so the emission spectrum for each element would contain a number of lines.[21]

Niels Bohr as a young man

Starting from only one simple assumption about the rule that the orbits must obey, the Bohr model was able to relate the observed spectral lines in the emission spectrum of hydrogen to previously known constants. In Bohr's model, the electron was not allowed to emit energy continuously and crash into the nucleus: once it was in the closest permitted orbit, it was stable forever. Bohr's model did not explain why the orbits should be quantized in that way, nor was it able to make accurate predictions for atoms with more than one electron, or to explain why some spectral lines are brighter than others.

Some fundamental assumptions of the Bohr model were soon proven wrong—but the key result that the discrete lines in emission spectra are due to some property of the electrons in atoms being quantized is correct. The way that the electrons actually behave is strikingly different from Bohr's atom, and from what we see in the world of our everyday experience; this modern quantum mechanical model of the atom is discussed below.

Louis de Broglie in 1929. De Broglie won the Nobel Prize in Physics for his prediction that matter acts as a wave, made in his 1924 PhD thesis.

Just as light has both wave-like and particle-like properties, matter also has wave-like properties.[22]

Matter behaving as a wave was first demonstrated experimentally for electrons: a beam of electrons can exhibit diffraction, just like a beam of light or a water wave.[note 8] Similar wave-like phenomena were later shown for atoms and even molecules.

The wavelength, λ, associated with any object is related to its momentum, p, through the Planck constant, h:[23][24]

${\displaystyle p={\frac {h}{\lambda }}.}$

The relationship, called the de Broglie hypothesis, holds for all types of matter: all matter exhibits properties of both particles and waves.

The concept of wave–particle duality says that neither the classical concept of "particle" nor of "wave" can fully describe the behavior of quantum-scale objects, either photons or matter. Wave–particle duality is an example of the principle of complementarity in quantum physics.[25][26][27][28][29] An elegant example of wave-particle duality, the double-slit experiment, is discussed in the section below.

The double-slit experiment

Main article: Double-slit experiment

The diffraction pattern produced when light is shone through one slit (top) and the interference pattern produced by two slits (bottom). The much more complex pattern from two slits, with its small-scale interference fringes, demonstrates the wave-like propagation of light.

In the double-slit experiment, as originally performed by Thomas Young in 1803,[30] and then Augustin Fresnel a decade later,[30] a beam of light is directed through two narrow, closely spaced slits, producing an interference pattern of light and dark bands on a screen. If one of the slits is covered up, one might naïvely expect that the intensity of the fringes due to interference would be halved everywhere. In fact, a much simpler pattern is seen, a diffraction pattern diametrically opposite the open slit. The same behavior can be demonstrated in water waves, and so the double-slit experiment was seen as a demonstration of the wave nature of light.

Variations of the double-slit experiment have been performed using electrons, atoms, and even large molecules,[31][32] and the same type of interference pattern is seen. Thus it has been demonstrated that all matter possesses both particle and wave characteristics.

Even if the source intensity is turned down, so that only one particle (e.g. photon or electron) is passing through the apparatus at a time, the same interference pattern develops over time. The quantum particle acts as a wave when passing through the double slits, but as a particle when it is detected. This is a typical feature of quantum complementarity: a quantum particle acts as a wave in an experiment to measure its wave-like properties, and like a particle in an experiment to measure its particle-like properties. The point on the detector screen where any individual particle shows up is the result of a random process. However, the distribution pattern of many individual particles mimics the diffraction pattern produced by waves.

In 1922, Otto Stern and Walther Gerlach shot silver atoms through an inhomogeneous magnetic field. Relative to its northern pole, pointing up, down, or somewhere in between, in classical mechanics, a magnet thrown through a magnetic field may be deflected a small or large distance upwards or downwards. The atoms that Stern and Gerlach shot through the magnetic field acted similarly. However, while the magnets could be deflected variable distances, the atoms would always be deflected a constant distance either up or down. This implied that the property of the atom that corresponds to the magnet's orientation must be quantized, taking one of two values (either up or down), as opposed to being chosen freely from any angle.

Ralph Kronig originated the theory that particles such as atoms or electrons behave as if they rotate, or "spin", about an axis. Spin would account for the missing magnetic moment, and allow two electrons in the same orbital to occupy distinct quantum states if they "spun" in opposite directions, thus satisfying the exclusion principle. The quantum number represented the sense (positive or negative) of spin.

The choice of the orientation of the magnetic field used in the Stern–Gerlach experiment is arbitrary. In the animation shown here, the field is vertical and so the atoms are deflected either up or down. If the magnet is rotated a quarter turn, the atoms are deflected either left or right. Using a vertical field shows that the spin along the vertical axis is quantized, and using a horizontal field shows that the spin along the horizontal axis is quantized.

If instead of hitting a detector screen, one of the beams of atoms coming out of the Stern–Gerlach apparatus is passed into another (inhomogeneous) magnetic field oriented in the same direction, all of the atoms are deflected the same way in this second field. However, if the second field is oriented at 90° to the first, then half of the atoms are deflected one way and half the other so that the atom's spin about the horizontal and vertical axes are independent of each other. However, if one of these beams (e.g. the atoms that were deflected up then left) is passed into a third magnetic field, oriented the same way as the first, half of the atoms go one way and half the other, even though they all went in the same direction originally. The action of measuring the atoms' spin concerning a horizontal field has changed their spin concerning a vertical field.

The Stern–Gerlach experiment demonstrates several important features of quantum mechanics:

• A feature of the natural world has been demonstrated to be quantized, and able to take only certain discrete values.
• Particles possess an intrinsic angular momentum that is closely analogous to the angular momentum of a classically spinning object.
• Measurement changes the system being measured in quantum mechanics. Only the spin of an object in one direction can be known, and observing the spin in another direction destroys the original information about the spin.
• Quantum mechanics is probabilistic: whether the spin of any individual atom sent into the apparatus is positive or negative is random.

In 1925, Werner Heisenberg attempted to solve one of the problems that the Bohr model left unanswered, explaining the intensities of the different lines in the hydrogen emission spectrum. Through a series of mathematical analogies, he wrote out the quantum-mechanical analog for the classical computation of intensities.[34] Shortly afterward, Heisenberg's colleague Max Born realized that Heisenberg's method of calculating the probabilities for transitions between the different energy levels could best be expressed by using the mathematical concept of matrices.[note 9]

In the same year, building on de Broglie's hypothesis, Erwin Schrödinger developed the equation that describes the behavior of a quantum-mechanical wave.[35] The mathematical model, called the Schrödinger equation after its creator, is central to quantum mechanics, defines the permitted stationary states of a quantum system, and describes how the quantum state of a physical system changes in time.[36] The wave itself is described by a mathematical function known as a "wave function". Schrödinger said that the wave function provides the "means for predicting the probability of measurement results".[37]

Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron as a classical wave, moving in a well of the electrical potential created by the proton. This calculation accurately reproduced the energy levels of the Bohr model.

In May 1926, Schrödinger proved that Heisenberg's matrix mechanics and his own wave mechanics made the same predictions about the properties and behavior of the electron; mathematically, the two theories had an underlying common form. Yet the two men disagreed on the interpretation of their mutual theory. For instance, Heisenberg accepted the theoretical prediction of jumps of electrons between orbitals in an atom,[38] but Schrödinger hoped that a theory based on continuous wave-like properties could avoid what he called (as paraphrased by Wilhelm Wien) "this nonsense about quantum jumps".[39] In the end, Heisenberg's approach won out, and quantum jumps were confirmed.[40]

The Niels Bohr Institute in Copenhagen, which was a focal point for researchers in quantum mechanics and related subjects in the 1920s and 1930s. Most of the world's best known theoretical physicists spent time there.

Bohr, Heisenberg, and others tried to explain what these experimental results and mathematical models really mean. Their description, known as the Copenhagen interpretation of quantum mechanics, aimed to describe the nature of reality that was being probed by the measurements and described by the mathematical formulations of quantum mechanics.

The main principles of the Copenhagen interpretation are:

1. A system is completely described by a wave function, usually represented by the Greek letter ${\displaystyle \psi }$ ("psi"). (Heisenberg)
2. How ${\displaystyle \psi }$ changes over time is given by the Schrödinger equation.
3. The description of nature is essentially probabilistic. The probability of an event—for example, where on the screen a particle shows up in the double-slit experiment—is related to the square of the absolute value of the amplitude of its wave function. (Born rule, due to Max Born, which gives a physical meaning to the wave function in the Copenhagen interpretation: the probability amplitude)
4. It is not possible to know the values of all of the properties of the system at the same time; those properties that are not known with precision must be described by probabilities. (Heisenberg's uncertainty principle)
5. Matter, like energy, exhibits a wave-particle duality. An experiment can demonstrate the particle-like properties of matter, or its wave-like properties; but not both at the same time. (Complementarity principle due to Bohr)
6. Measuring devices are essentially classical devices and measure classical properties such as position and momentum.
7. The quantum mechanical description of large systems should closely approximate the classical description. (Correspondence principle of Bohr and Heisenberg)

Various consequences of these principles are discussed in more detail in the following subsections.

Uncertainty principle

Main article: Uncertainty principle

Werner Heisenberg at the age of 26. Heisenberg won the Nobel Prize in Physics in 1932 for the work he did at around this time.[41]

Suppose it is desired to measure the position and speed of an object—for example, a car going through a radar speed trap. It can be assumed that the car has a definite position and speed at a particular moment in time. How accurately these values can be measured depends on the quality of the measuring equipment. If the precision of the measuring equipment is improved, it provides a result closer to the true value. It might be assumed that the speed of the car and its position could be operationally defined and measured simultaneously, as precisely as might be desired.

In 1927, Heisenberg proved that this last assumption is not correct.[42] Quantum mechanics shows that certain pairs of physical properties, for example, position and speed, cannot be simultaneously measured, nor defined in operational terms, to arbitrary precision: the more precisely one property is measured, or defined in operational terms, the less precisely can the other. This statement is known as the uncertainty principle. The uncertainty principle is not only a statement about the accuracy of our measuring equipment but, more deeply, is about the conceptual nature of the measured quantities—the assumption that the car had simultaneously defined position and speed does not work in quantum mechanics. On a scale of cars and people, these uncertainties are negligible, but when dealing with atoms and electrons they become critical.[43]

Heisenberg gave, as an illustration, the measurement of the position and momentum of an electron using a photon of light. In measuring the electron's position, the higher the frequency of the photon, the more accurate is the measurement of the position of the impact of the photon with the electron, but the greater is the disturbance of the electron. This is because from the impact with the photon, the electron absorbs a random amount of energy, rendering the measurement obtained of its momentum increasingly uncertain (momentum is velocity multiplied by mass), for one is necessarily measuring its post-impact disturbed momentum from the collision products and not its original momentum (momentum which should be simultaneously measured with position). With a photon of lower frequency, the disturbance (and hence uncertainty) in the momentum is less, but so is the accuracy of the measurement of the position of the impact.[44]

At the heart of the uncertainty principle is a fact that for any mathematical analysis in the position and velocity domains, achieving a sharper (more precise) curve in the position domain can only be done at the expense of a more gradual (less precise) curve in the speed domain, and vice versa. More sharpness in the position domain requires contributions from more frequencies in the speed domain to create the narrower curve, and vice versa. It is a fundamental tradeoff inherent in any such related or complementary measurements, but is only really noticeable at the smallest (Planck) scale, near the size of elementary particles.

The uncertainty principle shows mathematically that the product of the uncertainty in the position and momentum of a particle (momentum is velocity multiplied by mass) could never be less than a certain value, and that this value is related to Planck's constant.

The Pauli exclusion principle

Wolfgang Pauli

Main article: Pauli exclusion principle

In 1924, Wolfgang Pauli proposed a new quantum degree of freedom (or quantum number), with two possible values, to resolve inconsistencies between observed molecular spectra and the predictions of quantum mechanics. In particular, the spectrum of atomic hydrogen had a doublet, or pair of lines differing by a small amount, where only one line was expected. Pauli formulated his exclusion principle, stating, "There cannot exist an atom in such a quantum state that two electrons within [it] have the same set of quantum numbers."[45]

A year later, Uhlenbeck and Goudsmit identified Pauli's new degree of freedom with the property called spin whose effects were observed in the Stern–Gerlach experiment.

Application to the hydrogen atom

Main article: Atomic orbital model

Bohr's model of the atom was essentially a planetary one, with the electrons orbiting around the nuclear "sun". However, the uncertainty principle states that an electron cannot simultaneously have an exact location and velocity in the way that a planet does. Instead of classical orbits, electrons are said to inhabit atomic orbitals. An orbital is the "cloud" of possible locations in which an electron might be found, a distribution of probabilities rather than a precise location.[45] Each orbital is three dimensional, rather than the two-dimensional orbit, and is often depicted as a three-dimensional region within which there is a 95 percent probability of finding the electron.[46]

Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron as a wave, represented by the "wave function" Ψ, in an electric potential well, V, created by the proton. The solutions to Schrödinger's equation are distributions of probabilities for electron positions and locations. Orbitals have a range of different shapes in three dimensions. The energies of the different orbitals can be calculated, and they accurately match the energy levels of the Bohr model.

Within Schrödinger's picture, each electron has four properties:

1. An "orbital" designation, indicating whether the particle-wave is one that is closer to the nucleus with less energy or one that is farther from the nucleus with more energy;
2. The "shape" of the orbital, spherical or otherwise;
3. The "inclination" of the orbital, determining the magnetic moment of the orbital around the z-axis.
4. The "spin" of the electron.

The collective name for these properties is the quantum state of the electron. The quantum state can be described by giving a number to each of these properties; these are known as the electron's quantum numbers. The quantum state of the electron is described by its wave function. The Pauli exclusion principle demands that no two electrons within an atom may have the same values of all four numbers.

The shapes of atomic orbitals. Rows: 1s, 2p, 3d and 4f. From left to right ${\displaystyle m=-l,\ldots ,l}$. The colors show the phase of the wave function.

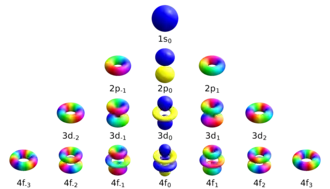
The first property describing the orbital is the principal quantum number, n, which is the same as in Bohr's model. n denotes the energy level of each orbital. The possible values for n are integers:

${\displaystyle n=1,2,3\ldots }$

The next quantum number, the azimuthal quantum number, denoted l, describes the shape of the orbital. The shape is a consequence of the angular momentum of the orbital. The angular momentum represents the resistance of a spinning object to speeding up or slowing down under the influence of external force. The azimuthal quantum number represents the orbital angular momentum of an electron around its nucleus. The possible values for l are integers from 0 to n − 1 (where n is the principal quantum number of the electron):

${\displaystyle l=0,1,\ldots ,n-1.}$

The shape of each orbital is usually referred to by a letter, rather than by its azimuthal quantum number. The first shape (l=0) is denoted by the letter s (a mnemonic being "sphere"). The next shape is denoted by the letter p and has the form of a dumbbell. The other orbitals have more complicated shapes (see atomic orbital), and are denoted by the letters d, f, g, etc.

The third quantum number, the magnetic quantum number, describes the magnetic moment of the electron, and is denoted by m_l (or simply m). The possible values for m_l are integers from −l to l (where l is the azimuthal quantum number of the electron):

${\displaystyle m_{l}=-l,-(l-1),\ldots ,0,\ldots ,(l-1),l.}$

The magnetic quantum number measures the component of the angular momentum in a particular direction. The choice of direction is arbitrary; conventionally the z-direction is chosen.

The fourth quantum number, the spin quantum number (pertaining to the "orientation" of the electron's spin) is denoted m_s, with values +1⁄2 or −1⁄2.

The chemist Linus Pauling wrote, by way of example:

In the case of a helium atom with two electrons in the 1s orbital, the Pauli Exclusion Principle requires that the two electrons differ in the value of one quantum number. Their values of n, l, and m_l are the same. Accordingly they must differ in the value of m_s, which can have the value of +1⁄2 for one electron and −1⁄2 for the other."[45]

It is the underlying structure and symmetry of atomic orbitals, and the way that electrons fill them, that leads to the organization of the periodic table. The way the atomic orbitals on different atoms combine to form molecular orbitals determines the structure and strength of chemical bonds between atoms.

Paul Dirac (1902–1984)

In 1928, Paul Dirac extended the Pauli equation, which described spinning electrons, to account for special relativity. The result was a theory that dealt properly with events, such as the speed at which an electron orbits the nucleus, occurring at a substantial fraction of the speed of light. By using the simplest electromagnetic interaction, Dirac was able to predict the value of the magnetic moment associated with the electron's spin and found the experimentally observed value, which was too large to be that of a spinning charged sphere governed by classical physics. He was able to solve for the spectral lines of the hydrogen atom and to reproduce from physical first principles Sommerfeld's successful formula for the fine structure of the hydrogen spectrum.

Dirac's equations sometimes yielded a negative value for energy, for which he proposed a novel solution: he posited the existence of an antielectron and a dynamical vacuum. This led to the many-particle quantum field theory.

Superposition of two quantum characteristics, and two resolution possibilities

The Pauli exclusion principle says that two electrons in one system cannot be in the same state. Nature leaves open the possibility, however, that two electrons can have both states "superimposed" over each of them. Recall that the wave functions that emerge simultaneously from the double slits arrive at the detection screen in a state of superposition. Nothing is certain until the superimposed waveforms "collapse". At that instant, an electron shows up somewhere in accordance with the probability that is the square of the absolute value of the sum of the complex-valued amplitudes of the two superimposed waveforms. The situation there is already very abstract. A concrete way of thinking about entangled photons, photons in which two contrary states are superimposed on each of them in the same event, is as follows:

Imagine that we have two color-coded states of photons: one state labeled blue and another state labeled red. Let the superposition of the red and the blue state appear (in imagination) as a purple state. We consider a case in which two photons are produced as the result of one single atomic event. Perhaps they are produced by the excitation of a crystal that characteristically absorbs a photon of a certain frequency and emits two photons of half the original frequency. In this case, the photons are interconnected via their shared origin in a single atomic event. This setup results in superimposed states of the photons. So the two photons come out purple. If the experimenter now performs some experiment that determines whether one of the photons is either blue or red, then that experiment changes the photon involved from one having a superposition of blue and red characteristics to a photon that has only one of those characteristics. The problem that Einstein had with such an imagined situation was that if one of these photons had been kept bouncing between mirrors in a laboratory on earth, and the other one had traveled halfway to the nearest star when its twin was made to reveal itself as either blue or red, that meant that the distant photon now had to lose its purple status too. So whenever it might be investigated after its twin had been measured, it would necessarily show up in the opposite state to whatever its twin had revealed.

In trying to show that quantum mechanics was not a complete theory, Einstein started with the theory's prediction that two or more particles that have interacted in the past can appear strongly correlated when their various properties are later measured. He sought to explain this seeming interaction classically, through their common past, and preferably not by some "spooky action at a distance". The argument is worked out in a famous paper, Einstein, Podolsky, and Rosen (1935; abbreviated EPR) setting out what is now called the EPR paradox. Assuming what is now usually called local realism, EPR attempted to show from quantum theory that a particle has both position and momentum simultaneously, while according to the Copenhagen interpretation, only one of those two properties actually exists and only at the moment that it is being measured. EPR concluded that quantum theory is incomplete in that it refuses to consider physical properties that objectively exist in nature. (Einstein, Podolsky, & Rosen 1935 is currently Einstein's most cited publication in physics journals.) In the same year, Erwin Schrödinger used the word "entanglement" and declared: "I would not call that one but rather the characteristic trait of quantum mechanics."[47] Ever since Irish physicist John Stewart Bell theoretically and experimentally disproved the "hidden variables" theory of Einstein, Podolsky, and Rosen, most physicists have accepted entanglement as a real phenomenon.[48] However, there is some minority dispute.[49] The Bell inequalities are the most powerful challenge to Einstein's claims.

The idea of quantum field theory began in the late 1920s with British physicist Paul Dirac, when he attempted to quantize the energy of the electromagnetic field; just like in quantum mechanics the energy of an electron in the hydrogen atom was quantized. Quantization is a procedure for constructing a quantum theory starting from a classical theory.

Merriam-Webster defines a field in physics as "a region or space in which a given effect (such as magnetism) exists".[50] Other effects that manifest themselves as fields are gravitation and static electricity.[51] In 2008, physicist Richard Hammond wrote:

Sometimes we distinguish between quantum mechanics (QM) and quantum field theory (QFT). QM refers to a system in which the number of particles is fixed, and the fields (such as the electromechanical field) are continuous classical entities. QFT ... goes a step further and allows for the creation and annihilation of particles ...

He added, however, that quantum mechanics is often used to refer to "the entire notion of quantum view".[52]^: 108

In 1931, Dirac proposed the existence of particles that later became known as antimatter.[53] Dirac shared the Nobel Prize in Physics for 1933 with Schrödinger "for the discovery of new productive forms of atomic theory".[54]

On its face, quantum field theory allows infinite numbers of particles and leaves it up to the theory itself to predict how many and with which probabilities or numbers they should exist. When developed further, the theory often contradicts observation, so that its creation and annihilation operators can be empirically tied down. Furthermore, empirical conservation laws such as that of mass–energy suggest certain constraints on the mathematical form of the theory, which are mathematically speaking finicky. The latter fact makes quantum field theories difficult to handle, but has also led to further restrictions on admissible forms of the theory; the complications are mentioned below under the rubric of renormalization.

Quantum electrodynamics (QED) is the name of the quantum theory of the electromagnetic force. Understanding QED begins with understanding electromagnetism. Electromagnetism can be called "electrodynamics" because it is a dynamic interaction between electrical and magnetic forces. Electromagnetism begins with the electric charge.

Electric charges are the sources of and create, electric fields. An electric field is a field that exerts a force on any particles that carry electric charges, at any point in space. This includes the electron, proton, and even quarks, among others. As a force is exerted, electric charges move, a current flows, and a magnetic field is produced. The changing magnetic field, in turn, causes electric current (often moving electrons). The physical description of interacting charged particles, electrical currents, electrical fields, and magnetic fields is called electromagnetism.

In 1928 Paul Dirac produced a relativistic quantum theory of electromagnetism. This was the progenitor to modern quantum electrodynamics, in that it had essential ingredients of the modern theory. However, the problem of unsolvable infinities developed in this relativistic quantum theory. Years later, renormalization largely solved this problem. Initially viewed as a provisional, suspect procedure by some of its originators, renormalization eventually was embraced as an important and self-consistent tool in QED and other fields of physics. Also, in the late 1940s Feynman's diagrams depicted all possible interactions on a given event. The diagrams showed in particular that the electromagnetic force is the exchange of photons between interacting particles.[55]

The Lamb shift is an example of a quantum electrodynamics prediction that has been experimentally verified. It is an effect whereby the quantum nature of the electromagnetic field makes the energy levels in an atom or ion deviate slightly from what they would otherwise be. As a result, spectral lines may shift or split.

Similarly, within a freely propagating electromagnetic wave, the current can also be just an abstract displacement current, instead of involving charge carriers. In QED, its full description makes essential use of short-lived virtual particles. There, QED again validates an earlier, rather mysterious concept.

In the 1960s physicists realized that QED broke down at extremely high energies. From this inconsistency the Standard Model of particle physics was discovered, which remedied the higher energy breakdown in theory. It is another extended quantum field theory that unifies the electromagnetic and weak interactions into one theory. This is called the electroweak theory.

Additionally, the Standard Model contains a high energy unification of the electroweak theory with the strong force, described by quantum chromodynamics. It also postulates a connection with gravity as yet another gauge theory, but the connection is as of 2015 still poorly understood. The theory's successful prediction of the Higgs particle to explain inertial mass was confirmed by the Large Hadron Collider,[56] and thus the Standard model is now considered the basic and more or less complete description of particle physics as we know it.

The physical measurements, equations, and predictions pertinent to quantum mechanics are all consistent and hold a very high level of confirmation. However, the question of what these abstract models say about the underlying nature of the real world has received competing answers. These interpretations are widely varying and sometimes somewhat abstract. For instance, the Copenhagen interpretation states that before a measurement, statements about a particle's properties are completely meaningless, while in the Many-worlds interpretation describes the existence of a multiverse made up of every possible universe.[57]

Applications of quantum mechanics include the laser, the transistor, the electron microscope, and magnetic resonance imaging. A special class of quantum mechanical applications is related to macroscopic quantum phenomena such as superfluid helium and superconductors. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.

In even the simple light switch, quantum tunneling is absolutely vital, as otherwise the electrons in the electric current could not penetrate the potential barrier made up of a layer of oxide. Flash memory chips found in USB drives also use quantum tunneling, to erase their memory cells.[58]

• Einstein's thought experiments
• Macroscopic quantum phenomena
• Philosophy of physics
• Quantum computing
• Virtual particle
• List of textbooks on classical and quantum mechanics

• Bernstein, Jeremy (2005). "Max Born and the quantum theory". American Journal of Physics. 73 (11): 999–1008. Bibcode:2005AmJPh..73..999B. doi:10.1119/1.2060717.
• Beller, Mara (2001). Quantum Dialogue: The Making of a Revolution. University of Chicago Press.
• Bohr, Niels (1958). Atomic Physics and Human Knowledge. John Wiley & Sons]. ISBN 0486479285. OCLC 530611.
• de Broglie, Louis (1953). The Revolution in Physics. Noonday Press. LCCN 53010401.
• Bronner, Patrick; Strunz, Andreas; Silberhorn, Christine; Meyn, Jan-Peter (2009). "Demonstrating quantum random with single photons". European Journal of Physics. 30 (5): 1189–1200. Bibcode:2009EJPh...30.1189B. doi:10.1088/0143-0807/30/5/026. S2CID 7903179.
• Einstein, Albert (1934). Essays in Science. Philosophical Library. ISBN 0486470113. LCCN 55003947.
• Feigl, Herbert; Brodbeck, May (1953). Readings in the Philosophy of Science. Appleton-Century-Crofts. ISBN 0390304883. LCCN 53006438.
• Feynman, Richard P. (1949). "Space-Time Approach to Quantum Electrodynamics". Physical Review. 76 (6): 769–89. Bibcode:1949PhRv...76..769F. doi:10.1103/PhysRev.76.769.
• Feynman, Richard P. (1990). QED, The Strange Theory of Light and Matter. Penguin Books. ISBN 978-0140125054.
• Fowler, Michael (1999). The Bohr Atom. University of Virginia.
• Heisenberg, Werner (1958). Physics and Philosophy. Harper and Brothers. ISBN 0061305499. LCCN 99010404.
• Lakshmibala, S. (2004). "Heisenberg, Matrix Mechanics and the Uncertainty Principle". Resonance: Journal of Science Education. 9 (8): 46–56. doi:10.1007/bf02837577. S2CID 29893512.
• Liboff, Richard L. (1992). Introductory Quantum Mechanics (2nd ed.). Addison-Wesley Pub. Co. ISBN 9780201547153.
• Lindsay, Robert Bruce; Margenau, Henry (1957). Foundations of Physics. Dover. ISBN 0918024188. LCCN 57014416.
• McEvoy, J. P.; Zarate, Oscar (2004). Introducing Quantum Theory. ISBN 1874166374.
• Nave, Carl Rod (2005). "Quantum Physics". HyperPhysics. Georgia State University.
• Peat, F. David (2002). From Certainty to Uncertainty: The Story of Science and Ideas in the Twenty-First Century. Joseph Henry Press.
• Reichenbach, Hans (1944). Philosophic Foundations of Quantum Mechanics. University of California Press. ISBN 0486404595. LCCN a44004471.
• Schilpp, Paul Arthur (1949). Albert Einstein: Philosopher-Scientist. Tudor Publishing Company. LCCN 50005340.
• Scientific American Reader, 1953.
• Sears, Francis Weston (1949). Optics (3rd ed.). Addison-Wesley. ISBN 0195046013. LCCN 51001018.
• Shimony, A. (1983). "(title not given in citation)". Foundations of Quantum Mechanics in the Light of New Technology (S. Kamefuchi et al., eds.). Tokyo: Japan Physical Society. p. 225.; cited in: Popescu, Sandu; Daniel Rohrlich (1996). "Action and Passion at a Distance: An Essay in Honor of Professor Abner Shimony". arXiv:quant-ph/9605004.
• Tavel, Morton; Tavel, Judith (illustrations) (2002). Contemporary physics and the limits of knowledge. Rutgers University Press. ISBN 978-0813530772.
• Van Vleck, J. H.,1928, "The Correspondence Principle in the Statistical Interpretation of Quantum Mechanics", Proc. Natl. Acad. Sci. 14: 179.
• Westmoreland; Benjamin Schumacher (1998). "Quantum Entanglement and the Nonexistence of Superluminal Signals". arXiv:quant-ph/9801014.
• Wheeler, John Archibald; Feynman, Richard P. (1949). "Classical Electrodynamics in Terms of Direct Interparticle Action" (PDF). Reviews of Modern Physics. 21 (3): 425–33. Bibcode:1949RvMP...21..425W. doi:10.1103/RevModPhys.21.425.
• Wieman, Carl; Perkins, Katherine (2005). "Transforming Physics Education". Physics Today. 58 (11): 36. Bibcode:2005PhT....58k..36W. doi:10.1063/1.2155756.

The following titles, all by working physicists, attempt to communicate quantum theory to laypeople, using a minimum of technical apparatus.

• Jim Al-Khalili (2003). Quantum: A Guide for the Perplexed. Weidenfeld & Nicolson. ISBN 978-1780225340.
• Chester, Marvin (1987). Primer of Quantum Mechanics. John Wiley. ISBN 0486428788.
• Brian Cox and Jeff Forshaw (2011) The Quantum Universe. Allen Lane. ISBN 978-1846144325.
• Richard Feynman (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 0691083886.
• Ford, Kenneth (2005). The Quantum World. Harvard Univ. Press. Includes elementary particle physics.
• Ghirardi, GianCarlo (2004). Sneaking a Look at God's Cards, Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using algebra, trigonometry, and bra–ket notation can be passed over on a first reading.
• Tony Hey and Walters, Patrick (2003). The New Quantum Universe. Cambridge Univ. Press. Includes much about the technologies quantum theory has made possible. ISBN 978-0521564571.
• Vladimir G. Ivancevic, Tijana T. Ivancevic (2008). Quantum leap: from Dirac and Feynman, Across the universe, to human body and mind. World Scientific Publishing Company. Provides an intuitive introduction in non-mathematical terms and an introduction in comparatively basic mathematical terms. ISBN 978-9812819277.
• J. P. McEvoy and Oscar Zarate (2004). Introducing Quantum Theory. Totem Books. ISBN 1840465778'
• N. David Mermin (1990). "Spooky actions at a distance: mysteries of the QT" in his Boojums all the way through. Cambridge Univ. Press: 110–76. The author is a rare physicist who tries to communicate to philosophers and humanists. ISBN 978-0521388801.
• Roland Omnès (1999). Understanding Quantum Mechanics. Princeton Univ. Press. ISBN 978-0691004358.
• Victor Stenger (2000). Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Buffalo NY: Prometheus Books. Chpts. 5–8. ISBN 978-1573928595.
• Martinus Veltman (2003). Facts and Mysteries in Elementary Particle Physics. World Scientific Publishing Company. ISBN 978-9812381491.

The Wikibook Quantum Mechanics has a page on the topic of: Introduction to Quantum Mechanics

• "Microscopic World – Introduction to Quantum Mechanics". by Takada, Kenjiro, Emeritus professor at Kyushu University
• The Quantum Exchange (tutorials and open-source learning software).
• Atoms and the Periodic Table
• Single and double slit interference
• Time-Evolution of a Wavepacket in a Square Well An animated demonstration of a wave packet dispersion over time.
• Carroll, Sean M. "Quantum Mechanics (an embarrassment)". Sixty Symbols. Brady Haran for the University of Nottingham.