Wave–particle duality

Wave–particle duality is the concept in quantum mechanics that every particle or quantum entity may be described as either a particle or a wave. It expresses the inability of the classical concepts "particle" or "wave" to fully describe the behaviour of quantum-scale objects. As Albert Einstein wrote:[1]

It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do.

Part of a series of articles about
Quantum mechanics
Schrödinger equation
Background
Fundamentals
Experiments
  • Quantum eraser
    • Delayed-choice
Formulations
  • Overview
Equations
Interpretations
  • Overview
  • Bayesian
  • Consistent histories
  • Copenhagen
  • de Broglie–Bohm
  • Ensemble
  • Hidden-variable
    • Local
  • Many-worlds
  • Objective collapse
  • Quantum logic
  • Relational
  • Transactional
Advanced topics
Scientists

Through the work of Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr, Erwin Schrödinger and many others, current scientific theory holds that all particles exhibit a wave nature and vice versa.[2] This phenomenon has been verified not only for elementary particles, but also for compound particles like atoms and even molecules. For macroscopic particles, because of their extremely short wavelengths, wave properties usually cannot be detected.[3]

Although the use of the wave–particle duality has worked well in physics, the meaning or interpretation has not been satisfactorily resolved; see interpretations of quantum mechanics.

Bohr regarded the "duality paradox" as a fundamental or metaphysical fact of nature. A given kind of quantum object will exhibit sometimes wave, sometimes particle, character, in respectively different physical settings. He saw such duality as one aspect of the concept of complementarity.[4] Bohr regarded renunciation of the cause-effect relation, or complementarity, of the space-time picture, as essential to the quantum mechanical account.[5]

Werner Heisenberg considered the question further. He saw the duality as present for all quantic entities, but not quite in the usual quantum mechanical account considered by Bohr. He saw it in what is called second quantization, which generates an entirely new concept of fields that exist in ordinary space-time, causality still being visualizable. Classical field values (e.g. the electric and magnetic field strengths of Maxwell) are replaced by an entirely new kind of field value, as considered in quantum field theory. Turning the reasoning around, ordinary quantum mechanics can be deduced as a specialized consequence of quantum field theory.[6][7]

History

Classical particle and wave theories of light
Thomas Young's sketch of two-slit diffraction of waves, 1803.

Democritus (5th century BC) argued that all things in the universe, including light, are composed of indivisible sub-components.[8] Euclid (4th–3rd century BC) gives treatises on light propagation, states the principle of shortest trajectory of light, including multiple reflections on mirrors, including spherical, while Plutarch (1st–2nd century AD) describes multiple reflections on spherical mirrors discussing the creation of larger or smaller images, real or imaginary, including the case of chirality of the images. At the beginning of the 11th century, the Arabic scientist Ibn al-Haytham wrote the first comprehensive Book of Optics describing reflection, refraction, and the operation of a pinhole lens via rays of light traveling from the point of emission to the eye. He asserted that these rays were composed of particles of light. In 1630, René Descartes popularized the opposing wave description in his treatise on light, The World, showing that the behaviour of light could be re-created by modeling wave-like disturbances in a universal medium i.e. luminiferous aether. Beginning in 1670 and progressing over three decades, Isaac Newton developed and championed his corpuscular theory, arguing that the perfectly straight lines of reflection demonstrated light's particle nature, only particles could travel in such straight lines. He explained refraction by positing that particles of light accelerated laterally upon entering a denser medium. Around the same time, Newton's contemporaries Robert Hooke and Christiaan Huygens, and later Augustin-Jean Fresnel, mathematically refined the wave viewpoint, showing that if light traveled at different speeds in different media, refraction could be easily explained as the medium-dependent propagation of light waves. The resulting Huygens–Fresnel principle was extremely successful at reproducing light's behaviour and was subsequently supported by Thomas Young's discovery of wave interference of light by his double-slit experiment in 1801.[9] The wave view did not immediately displace the ray and particle view, but began to dominate scientific thinking about light in the mid 19th century, since it could explain polarization phenomena that the alternatives could not.[10]

James Clerk Maxwell discovered that he could apply his previously discovered Maxwell's equations, along with a slight modification to describe self-propagating waves of oscillating electric and magnetic fields. It quickly became apparent that visible light, ultraviolet light, and infrared light were all electromagnetic waves of differing frequency.

  • Particle impacts make visible the interference pattern of waves.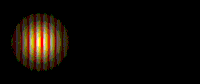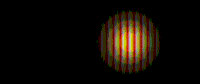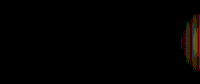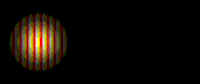
  • A quantum particle is represented by a wave packet.
  • Interference of a quantum particle with itself.

Black-body radiation and Planck's law
Main article: Black-body radiation

In 1901, Max Planck published an analysis that succeeded in reproducing the observed spectrum of light emitted by a glowing object. To accomplish this, Planck had to make a mathematical assumption of quantized energy of the oscillators, i.e. atoms of the black body that emit radiation. Einstein later proposed that electromagnetic radiation itself is quantized, not the energy of radiating atoms.

Black-body radiation, the emission of electromagnetic energy due to an object's heat, could not be explained from classical arguments alone. The equipartition theorem of classical mechanics, the basis of all classical thermodynamic theories, stated that an object's energy is partitioned equally among the object's vibrational modes. But applying the same reasoning to the electromagnetic emission of such a thermal object was not so successful. That thermal objects emit light had been long known. Since light was known to be waves of electromagnetism, physicists hoped to describe this emission via classical laws. This became known as the black body problem. Since the equipartition theorem worked so well in describing the vibrational modes of the thermal object itself, it was natural to assume that it would perform equally well in describing the radiative emission of such objects. But a problem quickly arose if each mode received an equal partition of energy, the short wavelength modes would consume all the energy. This became clear when plotting the Rayleigh–Jeans law, which, while correctly predicting the intensity of long wavelength emissions, predicted infinite total energy as the intensity diverges to infinity for short wavelengths. This became known as the ultraviolet catastrophe.

In 1900, Max Planck hypothesized that the frequency of light emitted by the black body depended on the frequency of the oscillator that emitted it, and the energy of these oscillators increased linearly with frequency (according E = hf where h is Planck's constant and f is the frequency). This was not an unsound proposal considering that macroscopic oscillators operate similarly when studying five simple harmonic oscillators of equal amplitude but different frequency, the oscillator with the highest frequency possesses the highest energy (though this relationship is not linear like Planck's). By demanding that high-frequency light must be emitted by an oscillator of equal frequency, and further requiring that this oscillator occupy higher energy than one of a lesser frequency, Planck avoided any catastrophe, giving an equal partition to high-frequency oscillators produced successively fewer oscillators and less emitted light. And as in the Maxwell–Boltzmann distribution, the low-frequency, low-energy oscillators were suppressed by the onslaught of thermal jiggling from higher energy oscillators, which necessarily increased their energy and frequency.

The most revolutionary aspect of Planck's treatment of the black body is that it inherently relies on an integer number of oscillators in thermal equilibrium with the electromagnetic field. These oscillators give their entire energy to the electromagnetic field, creating a quantum of light, as often as they are excited by the electromagnetic field, absorbing a quantum of light and beginning to oscillate at the corresponding frequency. Planck had intentionally created an atomic theory of the black body, but had unintentionally generated an atomic theory of light, where the black body never generates quanta of light at a given frequency with an energy less than hf. However, once realizing that he had quantized the electromagnetic field, he denounced particles of light as a limitation of his approximation, not a property of reality.

Photoelectric effect
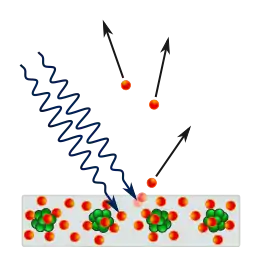
Main article: Photoelectric effect
The photoelectric effect. Incoming photons on the left strike a metal plate (bottom), and eject electrons, depicted as flying off to the right.

While Planck had solved the ultraviolet catastrophe by using atoms and a quantized electromagnetic field, most contemporary physicists agreed that Planck's "light quanta" represented only flaws in his model. A more-complete derivation of black-body radiation would yield a fully continuous and "wave-like" electromagnetic field with no quantization. However, in 1905 Albert Einstein took Planck's black body model to produce his solution to another outstanding problem of the day: the photoelectric effect, wherein electrons are emitted from atoms when they absorb energy from light. Since their existence was theorized eight years previously, phenomena had been studied with the electron model in mind in physics laboratories worldwide.

In 1902, Philipp Lenard discovered that the energy of these ejected electrons did not depend on the intensity of the incoming light, but instead on its frequency. So if one shines a little low-frequency light upon a metal, a few low energy electrons are ejected. If one now shines a very intense beam of low-frequency light upon the same metal, a whole slew of electrons are ejected; however they possess the same low energy, there are merely more of them. The more light there is, the more electrons are ejected. Whereas in order to get high energy electrons, one must illuminate the metal with high-frequency light. Like blackbody radiation, this was at odds with a theory invoking continuous transfer of energy between radiation and matter. However, it can still be explained using a fully classical description of light, as long as matter is quantum mechanical in nature.[11]

If one used Planck's energy quanta, and demanded that electromagnetic radiation at a given frequency could only transfer energy to matter in integer multiples of an energy quantum hf, then the photoelectric effect could be explained very simply. Low-frequency light only ejects low-energy electrons because each electron is excited by the absorption of a single photon. Increasing the intensity of the low-frequency light (increasing the number of photons) only increases the number of excited electrons, not their energy, because the energy of each photon remains low. Only by increasing the frequency of the light, and thus increasing the energy of the photons, can one eject electrons with higher energy. Thus, using Planck's constant h to determine the energy of the photons based upon their frequency, the energy of ejected electrons should also increase linearly with frequency, the gradient of the line being Planck's constant. These results were not confirmed until 1915, when Robert Andrews Millikan produced experimental results in perfect accord with Einstein's predictions.

While energy of ejected electrons reflected Planck's constant, the existence of photons was not explicitly proven until the discovery of the photon antibunching effect. This refers to the observation that once a single emitter (an atom, molecule, solid state emitter, etc.) radiates a detectable light signal, it cannot immediately release a second signal until after the emitter has been re-excited. This leads to a statistically quantifiable time delay between light emissions, so detection of multiple signals becomes increasingly unlikely as the observation time dips under the excited-state lifetime of the emitter.[12] The effect can be demonstrated in an undergraduate-level lab.[13]

This phenomenon could only be explained via photons. Einstein's "light quanta" would not be called photons until 1925, but even in 1905 they represented the quintessential example of wave–particle duality. Electromagnetic radiation propagates following linear wave equations, but can only be emitted or absorbed as discrete elements, thus acting as a wave and a particle simultaneously.

Einstein's explanation of photoelectric effect

In 1905, Albert Einstein provided an explanation of the photoelectric effect, an experiment that the wave theory of light failed to explain. He did so by postulating the existence of photons, quanta of light energy with particulate qualities.

In the photoelectric effect, it was observed that shining a light on certain metals would lead to an electric current in a circuit. Presumably, the light was knocking electrons out of the metal, causing current to flow. However, using the case of potassium as an example, it was also observed that while a dim blue light was enough to cause a current, even the strongest, brightest red light available with the technology of the time caused no current at all. According to the classical theory of light and matter, the strength or amplitude of a light wave was in proportion to its brightness: a bright light should have been easily strong enough to create a large current. Yet, oddly, this was not so.

Einstein explained this enigma by postulating that electrons can receive energy from an electromagnetic field only in discrete units (quanta or photons): an amount of energy E that was related to the frequency f of the light by

where h is Planck's constant (6.626 × 10−34 Js). Only photons of a high enough frequency (above a certain threshold value) could knock an electron free. For example, photons of blue light had sufficient energy to free an electron from the metal, but photons of red light did not. One photon of light above the threshold frequency could release only one electron; the higher the frequency of a photon, the higher the kinetic energy of the emitted electron, but no amount of light below the threshold frequency could release an electron. To violate this law would require extremely high-intensity lasers that had not yet been invented. Intensity-dependent phenomena have now been studied in detail with such lasers.[14]

Einstein was awarded the Nobel Prize in Physics in 1921 for his discovery of the law of the photoelectric effect.

de Broglie's hypothesis
Main article: Matter wave
Propagation of de Broglie waves in 1d—real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the colour opacity) of finding the particle at a given point x is spread out like a waveform; there is no definite position of the particle. As the amplitude increases above zero the curvature decreases, so the amplitude decreases again, and vice versa—the result is an alternating amplitude: a wave. Top: Plane wave. Bottom: Wave packet.

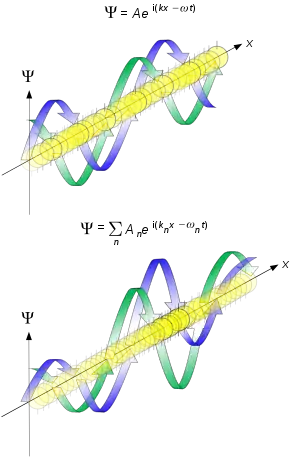
In 1924, Louis-Victor de Broglie formulated the de Broglie hypothesis, claiming that all matter[15][16] has a wave-like nature, he related wavelength and momentum:

This is a generalization of Einstein's equation above, since the momentum of a photon is given by p = and the wavelength (in a vacuum) by λ = , where c is the speed of light in vacuum.

De Broglie's formula was confirmed three years later for electrons with the observation of electron diffraction in two independent experiments. At the University of Aberdeen, George Paget Thomson passed a beam of electrons through a thin metal film and observed the predicted interference patterns. At Bell Labs, Clinton Joseph Davisson and Lester Halbert Germer guided the electron beam through a crystalline grid in their experiment popularly known as Davisson–Germer experiment.

De Broglie was awarded the Nobel Prize for Physics in 1929 for his hypothesis. Thomson and Davisson shared the Nobel Prize for Physics in 1937 for their experimental work.

Heisenberg's uncertainty principle
Main article: Uncertainty principle

In his work on formulating quantum mechanics, Werner Heisenberg postulated his uncertainty principle, which states:

where

here indicates standard deviation, a measure of spread or uncertainty;
x and p are a particle's position and linear momentum respectively.
is the reduced Planck's constant (Planck's constant divided by 2).

Heisenberg originally explained this as a consequence of the process of measuring: Measuring position accurately would disturb momentum and vice versa, offering an example (the "gamma-ray microscope") that depended crucially on the de Broglie hypothesis. The thought is now, however, that this only partly explains the phenomenon, but that the uncertainty also exists in the particle itself, even before the measurement is made.

In fact, the modern explanation of the uncertainty principle, extending the Copenhagen interpretation first put forward by Bohr and Heisenberg, depends even more centrally on the wave nature of a particle. Just as it is nonsensical to discuss the precise location of a wave on a string, particles do not have perfectly precise positions; likewise, just as it is nonsensical to discuss the wavelength of a "pulse" wave traveling down a string, particles do not have perfectly precise momenta that correspond to the inverse of wavelength. Moreover, when position is relatively well defined, the wave is pulse-like and has a very ill-defined wavelength, and thus momentum. And conversely, when momentum, and thus wavelength, is relatively well defined, the wave looks long and sinusoidal, and therefore it has a very ill-defined position.

de Broglie–Bohm theory
Couder experiments,[17] "materializing" the pilot wave model

De Broglie himself had proposed a pilot wave construct to explain the observed wave–particle duality. In this view, each particle has a well-defined position and momentum, but is guided by a wave function derived from Schrödinger's equation. The pilot wave theory was initially rejected because it generated non-local effects when applied to systems involving more than one particle. Non-locality, however, soon became established as an integral feature of quantum theory and David Bohm extended de Broglie's model to explicitly include it.

In the resulting representation, also called the de Broglie–Bohm theory or Bohmian mechanics,[18] the wave–particle duality vanishes, and explains the wave behaviour as a scattering with wave appearance, because the particle's motion is subject to a guiding equation or quantum potential.

This idea seems to me so natural and simple, to resolve the wave–particle dilemma in such a clear and ordinary way, that it is a great mystery to me that it was so generally ignored.[19] – J.S.Bell

The best illustration of the pilot-wave model was given by Couder's 2010 "walking droplets" experiments,[20] demonstrating the pilot-wave behaviour in a macroscopic mechanical analog.[17]

Wave nature of large objects

Since the demonstrations of wave-like properties in photons and electrons, similar experiments have been conducted with neutrons and protons. Among the most famous experiments are those of Estermann and Otto Stern in 1929.[21] Authors of similar recent experiments with atoms and molecules, described below, claim that these larger particles also act like waves.

A dramatic series of experiments emphasizing the action of gravity in relation to wave–particle duality was conducted in the 1970s using the neutron interferometer.[22] Neutrons, one of the components of the atomic nucleus, provide much of the mass of a nucleus and thus of ordinary matter. In the neutron interferometer, they act as quantum-mechanical waves directly subject to the force of gravity. While the results were not surprising since gravity was known to act on everything, including light (see tests of general relativity and the Pound–Rebka falling photon experiment), the self-interference of the quantum mechanical wave of a massive fermion in a gravitational field had never been experimentally confirmed before.

In 1999, the diffraction of C60 fullerenes by researchers from the University of Vienna was reported.[23] Fullerenes are comparatively large and massive objects, having an atomic mass of about 720 u. The de Broglie wavelength of the incident beam was about 2.5 pm, whereas the diameter of the molecule is about 1 nm, about 400 times larger. In 2012, these far-field diffraction experiments could be extended to phthalocyanine molecules and their heavier derivatives, which are composed of 58 and 114 atoms respectively. In these experiments the build-up of such interference patterns could be recorded in real time and with single molecule sensitivity.[24]

In 2003, the Vienna group also demonstrated the wave nature of tetraphenylporphyrin[25]—a flat biodye with an extension of about 2 nm and a mass of 614 u. For this demonstration they employed a near-field Talbot Lau interferometer.[26][27] In the same interferometer they also found interference fringes for C60F48, a fluorinated buckyball with a mass of about 1600 u, composed of 108 atoms.[25] Large molecules are already so complex that they give experimental access to some aspects of the quantum-classical interface, i.e., to certain decoherence mechanisms.[28][29] In 2011, the interference of molecules as heavy as 6910 u could be demonstrated in a Kapitza–Dirac–Talbot–Lau interferometer.[30] In 2013, the interference of molecules beyond 10,000 u has been demonstrated.[31]

Whether objects heavier than the Planck mass (about the weight of a large bacterium) have a de Broglie wavelength is theoretically unclear and experimentally unreachable; above the Planck mass a particle's Compton wavelength would be smaller than the Planck length and its own Schwarzschild radius, a scale at which current theories of physics may break down or need to be replaced by more general ones.[32]

Couder, Fort, et al. showed[33] that macroscopic oil droplets on a vibrating fluid bath can be used as an analogue model of wave–particle duality; a localized droplet creates periodical wave field around itself. Resonant interaction between the droplet and its own wave field exhibits behaviour analogous to quantum particles: interference in double-slit experiment,[34] unpredictable tunneling[35] (depending in complicated way on practically hidden state of field), orbit quantization[36] (that particle has to 'find a resonance' with field perturbations it creates—after one orbit, its internal phase has to return to the initial state) and Zeeman effect.[37] Note that other single and double slit experiments [38][39] have shown that wall-droplet interactions rather than diffraction or interference of the pilot wave may be responsible for the observed hydrodynamic patterns, which are different from slit-induced interference patterns exhibited by quantum particles.

Importance

Wave–particle duality is deeply embedded into the foundations of quantum mechanics. In the formalism of the theory, all the information about a particle is encoded in its wave function, a complex-valued function roughly analogous to the amplitude of a wave at each point in space. This function evolves according to Schrödinger equation. For particles with mass this equation has solutions that follow the form of the wave equation. Propagation of such waves leads to wave-like phenomena such as interference and diffraction. Particles without mass, like photons, have no solutions of the Schrödinger equation. Instead of a particle wave function that localizes mass in space, a photon wave function can be constructed from Einstein kinematics to localize energy in spatial coordinates.[40]

The particle-like behaviour is most evident due to phenomena associated with measurement in quantum mechanics. Upon measuring the location of the particle, the particle will be forced into a more localized state as given by the uncertainty principle. When viewed through this formalism, the measurement of the wave function will randomly lead to wave function collapse to a sharply peaked function at some location. For particles with mass, the likelihood of detecting the particle at any particular location is equal to the squared amplitude of the wave function there. The measurement will return a well-defined position, and is subject to Heisenberg's uncertainty principle.

Following the development of quantum field theory the ambiguity disappeared. The field permits solutions that follow the wave equation, which are referred to as the wave functions. The term particle is used to label the irreducible representations of the Lorentz group that are permitted by the field. An interaction as in a Feynman diagram is accepted as a calculationally convenient approximation where the outgoing legs are known to be simplifications of the propagation and the internal lines are for some order in an expansion of the field interaction. Since the field is non-local and quantized, the phenomena that previously were thought of as paradoxes are explained. Within the limits of the wave–particle duality the quantum field theory gives the same results.

Visualization

There are two ways to visualize the wave-particle behaviour: by the standard model and by the de Broglie–Bohr theory.

Below is an illustration of wave–particle duality as it relates to de Broglie's hypothesis and Heisenberg's Uncertainty principle, in terms of the position and momentum space wavefunctions for one spinless particle with mass in one dimension. These wavefunctions are Fourier transforms of each other.

The more localized the position-space wavefunction, the more likely the particle is to be found with the position coordinates in that region, and correspondingly the momentum-space wavefunction is less localized so the possible momentum components the particle could have are more widespread.

Conversely, the more localized the momentum-space wavefunction, the more likely the particle is to be found with those values of momentum components in that region, and correspondingly the less localized the position-space wavefunction, so the position coordinates the particle could occupy are more widespread.

Position x and momentum p wavefunctions corresponding to quantum particles. The colour opacity of the particles corresponds to the probability density of finding the particle with position x or momentum component p.
Top: If wavelength λ is unknown, so are momentum p, wave-vector k and energy E (de Broglie relations). As the particle is more localized in position space, Δx is smaller than for Δpx.
Bottom: If λ is known, so are p, k, and E. As the particle is more localized in momentum space, Δp is smaller than for Δx.

Alternative views

Wave–particle duality is an ongoing conundrum in modern physics. Most physicists accept wave–particle duality as the best explanation for a broad range of observed phenomena; however, it is not without controversy. Alternative views are also presented here. These views are not generally accepted by mainstream physics, but serve as a basis for valuable discussion within the community.

Both-particle-and-wave view

The pilot wave model, was originally developed by Louis de Broglie and further developed by David Bohm into the hidden variable theory. The phrase “hidden variable” is misleading since the variable in question is the positions of the particles.[41] Instead of duality, the pilot wave model proposes that both wave and particle are present with the wave guiding the particle in a deterministic fashion. The wave in question is the wavefunction obeying Schrödinger’s equation. Bohm’s formulation is intended to be classical, but it has to incorporate a distinctly non-classical feature: a nonlocal force ("quantum potential") acting on the particles.

Bohm’s original purpose (1952) “was to show that an alternative to the Copenhagen interpretation is at least logically possible.[42] Soon after he set the project aside and did not revive it until he met Basil Hiley in 1961 when both were at Birbeck College (University of London). Bohm and Hiley then wrote extensively on the theory and it gained a wider audience. This idea is held by a significant minority within the physics community.[43]

The Afshar experiment[44] (2007) may suggest that it is possible to simultaneously observe both wave and particle properties of photons. This claim is, however, disputed by other scientists.[45][46][47][48]

Wave-only view

Carver Mead, an American scientist and professor at Caltech, said that the duality can be replaced by a "wave-only" view. In his book Collective Electrodynamics: Quantum Foundations of Electromagnetism (2000), Mead purports to analyze the behaviour of electrons and photons purely in terms of electron wave functions, and attributes the apparent particle-like behaviour to quantization effects and eigenstates. According to reviewer David Haddon:[49]

Mead has cut the Gordian knot of quantum complementarity. He claims that atoms, with their neutrons, protons, and electrons, are not particles at all but pure waves of matter. Mead cites as the gross evidence of the exclusively wave nature of both light and matter the discovery between 1933 and 1996 of ten examples of pure wave phenomena, including the ubiquitous laser of CD players, the self-propagating electrical currents of superconductors, and the Bose–Einstein condensate of atoms.

Albert Einstein, who, in his search for a Unified Field Theory, did not accept wave–particle duality, wrote:[50]

This double nature of radiation (and of material corpuscles) ... has been interpreted by quantum-mechanics in an ingenious and amazingly successful fashion. This interpretation ... appears to me as only a temporary way out...

The many-worlds interpretation (MWI) is sometimes presented as a waves-only theory, including by its originator, Hugh Everett who referred to MWI as "the wave interpretation".[51]

The three wave hypothesis of R. Horodecki relates the particle to wave.[52][53] The hypothesis implies that a massive particle is an intrinsically spatially, as well as temporally extended, wave phenomenon by a nonlinear law.

The deterministic collapse theory[54] considers collapse and measurement as two independent physical processes. Collapse occurs when two wavepackets spatially overlap and satisfy a mathematical criterion, which depends on the parameters of both wavepackets. It is a contraction to the overlap volume. In a measurement apparatus one of the two wavepackets is one of the atomic clusters, which constitute the apparatus, and the wavepackets collapse to at most the volume of such a cluster. This mimics the action of a point particle.

Particle-only view

Still in the days of the old quantum theory, a pre-quantum-mechanical version of wave–particle duality was pioneered by William Duane,[55] and developed by others including Alfred Landé.[56] Duane explained diffraction of x-rays by a crystal in terms solely of their particle aspect. The deflection of the trajectory of each diffracted photon was explained as due to quantized momentum transfer from the spatially regular structure of the diffracting crystal.[57]

Neither-wave-nor-particle view

It has been argued that there are never exact particles or waves, but only some compromise or intermediate between them. For this reason, in 1928 Arthur Eddington[58] coined the name "wavicle" to describe the objects although it is not regularly used today. One consideration is that zero-dimensional mathematical points cannot be observed. Another is that the formal representation of such points, the Dirac delta function is unphysical, because it cannot be normalized. Parallel arguments apply to pure wave states. Roger Penrose states:[59]

Such 'position states' are idealized wavefunctions in the opposite sense from the momentum states. Whereas the momentum states are infinitely spread out, the position states are infinitely concentrated. Neither is normalizable [...].

Uses

Although it is difficult to draw a line separating wave–particle duality from the rest of quantum mechanics, it is nevertheless possible to list some applications of this basic idea.

  • Wave–particle duality is exploited in electron microscopy, where the small wavelengths associated with the electron can be used to view objects much smaller than what is visible using visible light.
  • Similarly, neutron diffraction uses neutrons with a wavelength of about 0.1 nm, the typical spacing of atoms in a solid, to determine the structure of solids.
  • Photos are now able to show this dual nature, which may lead to new ways of examining and recording this behaviour.[60]

See also
  • Arago spot
  • Afshar experiment
  • Basic concepts of quantum mechanics
  • Complementarity (physics)
  • Einstein's thought experiments
  • Englert–Greenberger–Yasin duality relation
  • EPR paradox
  • Faraday wave
  • Hanbury Brown and Twiss effect
  • Kapitsa–Dirac effect
  • Photon polarization
  • Scattering theory
  • Wavelet
  • Wheeler's delayed choice experiment

References
  1. Albert Einstein, Leopold Infeld (1938). The Evolution of Physics: The Growth of Ideas from Early Concepts to Relativity and Quanta. Cambridge University Press. Bibcode:1938epgi.book.....E.{{cite book}}: CS1 maint: uses authors parameter (link) Quoted in Harrison, David (2002). "Complementarity and the Copenhagen Interpretation of Quantum Mechanics". UPSCALE. Dept. of Physics, U. of Toronto. Retrieved 2008-06-21.
  2. Walter Greiner (2001). Quantum Mechanics: An Introduction. Springer. ISBN 978-3-540-67458-0.
  3. R. Eisberg & R. Resnick (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.). John Wiley & Sons. pp. 59–60. ISBN 978-0-471-87373-0. For both large and small wavelengths, both matter and radiation have both particle and wave aspects.... But the wave aspects of their motion become more difficult to observe as their wavelengths become shorter.... For ordinary macroscopic particles the mass is so large that the momentum is always sufficiently large to make the de Broglie wavelength small enough to be beyond the range of experimental detection, and classical mechanics reigns supreme.
  4. Kumar, Manjit (2011). Quantum: Einstein, Bohr, and the Great Debate about the Nature of Reality (Reprint ed.). W. W. Norton & Company. pp. 242, 375–376. ISBN 978-0-393-33988-8.
  5. Bohr, N. (1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Nature. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0.
  6. Camilleri, K. (2009). Heisenberg and the Interpretation of Quantum Mechanics: the Physicist as Philosopher, Cambridge University Press, Cambridge UK, ISBN 978-0-521-88484-6.
  7. Preparata, G. (2002). An Introduction to a Realistic Quantum Physics, World Scientific, River Edge NJ, ISBN 978-981-238-176-7.
  8. Berryman, Sylvia (2016), "Democritus", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Winter 2016 ed.), Metaphysics Research Lab, Stanford University, retrieved 2022-07-17
  9. Young, Thomas (1804). "Bakerian Lecture: Experiments and calculations relative to physical optics". Philosophical Transactions of the Royal Society. 94: 1–16. Bibcode:1804RSPT...94....1Y. doi:10.1098/rstl.1804.0001. S2CID 110408369.
  10. Buchwald, Jed (1989). The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. Chicago: University of Chicago Press. ISBN 978-0-226-07886-1. OCLC 18069573.
  11. Lamb, Willis E.; Scully, Marlan O. (1968). "The photoelectric effect without photons" (PDF).
  12. Wolf, Sebastian; Richter, Stefan (2020). "Light of Two Atoms in Free Space: Bunching or Antibunching?". Phys. Rev. Lett. 124 (6): 063603. arXiv:1911.10983. Bibcode:2020PhRvL.124f3603W. doi:10.1103/PhysRevLett.124.063603. PMID 32109104. S2CID 208267576.
  13. Thorn, J. J.; Neel, M. S.; Donato, V. W.; Bergreen, G. S.; Davies, R. E.; Beck, M. (2004). "Observing the quantum behaviour of light in an undergraduate laboratory". American Journal of Physics. 72 (9): 1210. Bibcode:2004AmJPh..72.1210T. doi:10.1119/1.1737397.
  14. Zhang, Q (1996). "Intensity dependence of the photoelectric effect induced by a circularly polarized laser beam". Physics Letters A. 216 (1–5): 125–128. Bibcode:1996PhLA..216..125Z. doi:10.1016/0375-9601(96)00259-9.
  15. Donald H Menzel, "Fundamental formulas of Physics", vol. 1, p. 153; Gives the de Broglie wavelengths for composite particles such as protons and neutrons.
  16. Brian Greene, The Elegant Universe, page 104 "all matter has a wave-like character"
  17. See this Science Channel production (Season II, Episode VI "How Does The Universe Work?"), presented by Morgan Freeman, https://www.youtube.com/watch?v=W9yWv5dqSKk
  18. Bohmian Mechanics, Stanford Encyclopedia of Philosophy.
  19. Bell, J. S., "Speakable and Unspeakable in Quantum Mechanics", Cambridge: Cambridge University Press, 1987.
  20. Couder, Y. (2010). "Walking droplets, a form of wave–particle duality at macroscopic scale?" (PDF). Europhysics News. 41 (1): 14–18. Bibcode:2010ENews..41a..14C. doi:10.1051/epn/2010101.
  21. Estermann, I.; Stern O. (1930). "Beugung von Molekularstrahlen". Zeitschrift für Physik. 61 (1–2): 95–125. Bibcode:1930ZPhy...61...95E. doi:10.1007/BF01340293. S2CID 121757478.
  22. Colella, R.; Overhauser, A. W.; Werner, S. A. (1975). "Observation of Gravitationally Induced Quantum Interference" (PDF). Physical Review Letters. 34 (23): 1472–1474. Bibcode:1975PhRvL..34.1472C. doi:10.1103/PhysRevLett.34.1472.
  23. Arndt, Markus; O. Nairz; J. Voss-Andreae, C. Keller, G. van der Zouw, A. Zeilinger (14 October 1999). "Wave–particle duality of C60". Nature. 401 (6754): 680–682. Bibcode:1999Natur.401..680A. doi:10.1038/44348. PMID 18494170. S2CID 4424892.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  24. Juffmann, Thomas; et al. (25 March 2012). "Real-time single-molecule imaging of quantum interference". Nature Nanotechnology. 7 (5): 297–300. arXiv:1402.1867. Bibcode:2012NatNa...7..297J. doi:10.1038/nnano.2012.34. PMID 22447163. S2CID 5918772.
  25. Hackermüller, Lucia; Stefan Uttenthaler; Klaus Hornberger; Elisabeth Reiger; Björn Brezger; Anton Zeilinger; Markus Arndt (2003). "The wave nature of biomolecules and fluorofullerenes". Phys. Rev. Lett. 91 (9): 090408. arXiv:quant-ph/0309016. Bibcode:2003PhRvL..91i0408H. doi:10.1103/PhysRevLett.91.090408. PMID 14525169. S2CID 13533517.
  26. Clauser, John F.; S. Li (1994). "Talbot von Lau interefometry with cold slow potassium atoms". Phys. Rev. A. 49 (4): R2213–2217. Bibcode:1994PhRvA..49.2213C. doi:10.1103/PhysRevA.49.R2213. PMID 9910609.
  27. Brezger, Björn; Lucia Hackermüller; Stefan Uttenthaler; Julia Petschinka; Markus Arndt; Anton Zeilinger (2002). "Matter-wave interferometer for large molecules". Phys. Rev. Lett. 88 (10): 100404. arXiv:quant-ph/0202158. Bibcode:2002PhRvL..88j0404B. doi:10.1103/PhysRevLett.88.100404. PMID 11909334. S2CID 19793304.
  28. Hornberger, Klaus; Stefan Uttenthaler; Björn Brezger; Lucia Hackermüller; Markus Arndt; Anton Zeilinger (2003). "Observation of Collisional Decoherence in Interferometry". Phys. Rev. Lett. 90 (16): 160401. arXiv:quant-ph/0303093. Bibcode:2003PhRvL..90p0401H. doi:10.1103/PhysRevLett.90.160401. PMID 12731960. S2CID 31057272.
  29. Hackermüller, Lucia; Klaus Hornberger; Björn Brezger; Anton Zeilinger; Markus Arndt (2004). "Decoherence of matter waves by thermal emission of radiation". Nature. 427 (6976): 711–714. arXiv:quant-ph/0402146. Bibcode:2004Natur.427..711H. doi:10.1038/nature02276. PMID 14973478. S2CID 3482856.
  30. Gerlich, Stefan; et al. (2011). "Quantum interference of large organic molecules". Nature Communications. 2 (263): 263. Bibcode:2011NatCo...2..263G. doi:10.1038/ncomms1263. PMC 3104521. PMID 21468015.
  31. Eibenberger, S.; Gerlich, S.; Arndt, M.; Mayor, M.; Tüxen, J. (2013). "Matter–wave interference of particles selected from a molecular library with masses exceeding 10 000 amu". Physical Chemistry Chemical Physics. 15 (35): 14696–14700. arXiv:1310.8343. Bibcode:2013PCCP...1514696E. doi:10.1039/c3cp51500a. PMID 23900710. S2CID 3944699.
  32. Peter Gabriel Bergmann, The Riddle of Gravitation, Courier Dover Publications, 1993 ISBN 0-486-27378-4 online
  33. Yves Couder Explains Wave/Particle Duality via Silicon Droplets – You Tube
  34. Couder, Yves; Fort, Emmanuel (2006). "Single-Particle Diffraction and Interference at a Macroscopic Scale". Physical Review Letters. 97 (15): 154101. Bibcode:2006PhRvL..97o4101C. doi:10.1103/PhysRevLett.97.154101. PMID 17155330.
  35. Eddi, A.; Fort, E.; Moisy, F.; Couder, Y. (2009). "Unpredictable Tunneling of a Classical Wave-Particle Association". Physical Review Letters. 102 (24): 240401. Bibcode:2009PhRvL.102x0401E. doi:10.1103/PhysRevLett.102.240401. PMID 19658983.
  36. Fort, E.; Eddi, A.; Boudaoud, A.; Moukhtar, J.; Couder, Y. (2010). "Path-memory induced quantization of classical orbits". PNAS. 107 (41): 17515–17520. arXiv:1307.6051. Bibcode:2010PNAS..10717515F. doi:10.1073/pnas.1007386107. PMC 2955113. S2CID 53462533.
  37. Eddi, A.; Moukhtar, J.; Perrard, S.; Fort, E.; Couder, Y. (2012). "Level Splitting at Macroscopic Scale". Physical Review Letters. 108 (26): 264503. Bibcode:2012PhRvL.108z4503E. doi:10.1103/PhysRevLett.108.264503. PMID 23004988.
  38. Pucci, G. (2018). "Walking droplets interacting with single and double slits" (PDF). Journal of Fluid Mechanics. 835 (835): 1136–1156. Bibcode:2018JFM...835.1136P. doi:10.1017/jfm.2017.790. S2CID 37760205.
  39. Andersen, Anders (2016). "Double-slit experiment with single wave-driven particles and its relation to quantum mechanics". Phys. Rev. E. 92 (1): 013006. doi:10.1103/PhysRevE.92.013006. PMID 26274269.
  40. Smith, Brian J; Raymer2, M G (2007). "Photon wave functions, wave-packet quantization of light, and coherence theory". New Journal of Physics. 9 (11): 414. arXiv:0708.0831. Bibcode:2007NJPh....9..414S. doi:10.1088/1367-2630/9/11/414.
  41. Goldstein, Sheldon. "The Defining Equations of Bohmian Mechanics". Stanford Encyclopedia of Philosophy. Retrieved 22 October 2021.
  42. Bohm, David (1952). "A Suggested Interpretation of the Quantum Theory in Terms of 'Hidden' Variables, I and II". Physical Review. 85 (2): 166–179. doi:10.1103/PhysRev.85.166.
  43. Buchanan, M. (2019). "In search of lost memories". Nat. Phys. 15 (5): 29–31. Bibcode:2019NatPh..15..420B. doi:10.1038/s41567-019-0521-9. S2CID 155305346.
  44. Afshar, S.S.; et al. (2007). "Paradox in Wave Particle Duality". Found. Phys. 37 (2): 295. arXiv:quant-ph/0702188. Bibcode:2007FoPh...37..295A. doi:10.1007/s10701-006-9102-8. S2CID 2161197.
  45. Kastner, R (2005). "Why the Afshar experiment does not refute complementarity". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 36 (4): 649–658. arXiv:quant-ph/0502021. Bibcode:2005SHPMP..36..649K. doi:10.1016/j.shpsb.2005.04.006. S2CID 119438183.
  46. Steuernagel, Ole (2007-08-03). "Afshar's Experiment Does Not Show a Violation of Complementarity". Foundations of Physics. 37 (9): 1370–1385. arXiv:quant-ph/0512123. Bibcode:2007FoPh...37.1370S. doi:10.1007/s10701-007-9153-5. ISSN 0015-9018. S2CID 53056142.
  47. Jacques, V.; Lai, N. D.; Dréau, A.; Zheng, D.; Chauvat, D.; Treussart, F.; Grangier, P.; Roch, J.-F. (2008-01-01). "Illustration of quantum complementarity using single photons interfering on a grating". New Journal of Physics. 10 (12): 123009. arXiv:0807.5079. Bibcode:2008NJPh...10l3009J. doi:10.1088/1367-2630/10/12/123009. ISSN 1367-2630. S2CID 2627030.
  48. Georgiev, Danko (2012-01-26). "Quantum Histories and Quantum Complementarity". ISRN Mathematical Physics. 2012: 1–37. doi:10.5402/2012/327278.
  49. David Haddon. "Recovering Rational Science". Touchstone. Retrieved 2007-09-12.
  50. Paul Arthur Schilpp, ed, Albert Einstein: Philosopher-Scientist, Open Court (1949), ISBN 0-87548-133-7, p. 51.
  51. See section VI(e) of Everett's thesis: The Theory of the Universal Wave Function, in Bryce Seligman DeWitt, R. Neill Graham, eds, The Many-Worlds Interpretation of Quantum Mechanics, Princeton Series in Physics, Princeton University Press (1973), ISBN 0-691-08131-X, pp. 3–140.
  52. Horodecki, R. (1981). "De broglie wave and its dual wave". Phys. Lett. A. 87 (3): 95–97. Bibcode:1981PhLA...87...95H. doi:10.1016/0375-9601(81)90571-5.
  53. Horodecki, R. (1983). "Superluminal singular dual wave". Lettere al Nuovo Cimento. 38 (15): 509–511. doi:10.1007/BF02817964. S2CID 120784358.
  54. Jabs, Arthur (2016). "A conjecture concerning determinism, reduction, and measurement in quantum mechanics". Quantum Studies: Mathematics and Foundations. 3 (4): 279–292. arXiv:1204.0614. doi:10.1007/s40509-016-0077-7. S2CID 32523066.
  55. Duane, W. (1923). "The Transfer in Quanta of Radiation Momentum to Matter". Proceedings of the National Academy of Sciences of the United States of America. 9 (5): 158–164. Bibcode:1923PNAS....9..158D. doi:10.1073/pnas.9.5.158. PMC 1085314. PMID 16576688.
  56. Landé, A. (1951). Quantum Mechanics, Sir Isaac Pitman and Sons, London, pp. 19–22.
  57. Heisenberg, W. (1930). The Physical Principles of the Quantum Theory, translated by C. Eckart and F.C. Hoyt, University of Chicago Press, Chicago, pp. 77–78.
  58. Eddington, Arthur Stanley (1928). The Nature of the Physical World. Cambridge, UK: MacMillan. pp. 201.
  59. Penrose, Roger (2007). The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage. p. 521, §21.10. ISBN 978-0-679-77631-4.
  60. Papageorgiou, Nik (2 March 2015). "Press release: The first ever photograph of light as both a particle and wave". Ecole Polytechnique Federale de Lausanne. {{cite journal}}: Cite journal requires |journal= (help)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.