0,999…
En matemáticas, 0,999... (siendo la coma un separador decimal) es el número decimal periódico que denota al número 1. En otras palabras, los símbolos «0,999...» y «1» son dos representaciones distintas del mismo número real.[1] Las demostraciones matemáticas de esta igualdad han sido formuladas con diferentes grados de rigor, dependiendo del método elegido para definir los números reales, las hipótesis y suposiciones de partida, el contexto histórico o el público al que se dirige.
El hecho de que ciertos números reales puedan ser representados por más de una secuencia de dígitos no se limita al sistema decimal únicamente. El mismo fenómeno ocurre en todas las bases enteras, y los matemáticos también han cuantificado los modos de escribir 1 en bases no enteras. Ni siquiera se trata de un fenómeno restringido al número 1: todo número decimal finito no nulo tiene un gemelo con infinitos nueves, por ejemplo: 2 y 1,999... representan al número natural dos; 28,3287 y 28,3286999... también representan al mismo número decimal. Por simplicidad, el decimal finito es casi siempre la representación preferida, lo que puede contribuir a una equivocada interpretación de que es la única representación. Por otra parte, la forma no terminal de un número permite estudiar más fácilmente los patrones de la expansión decimal de ciertas fracciones; en base tres, por ejemplo, permite expresar la estructura ternaria del conjunto de Cantor, un fractal simple. La representación múltiple debe tomarse en cuenta en la demostración clásica de la no numerabilidad de los números reales. De manera más general, cualquier sistema de numeración posicional de los números reales, contiene una cantidad infinita de números con representaciones múltiples.
La igualdad 0,999... = 1 ha sido aceptada desde hace tiempo por los matemáticos y se la incluye en los libros de texto. No ha sido hasta las últimas décadas en que los enseñantes de matemática se han inclinado por estudiar la percepción de esta igualdad entre los estudiantes, muchos de los cuales inicialmente la cuestionan o la niegan. Muchos se persuaden por una apelación a la autoridad de los libros de texto y los profesores, o por razonamientos aritméticos. Sin embargo, algunos no se conforman, por lo que buscan una justificación ulterior.
La igualdad 0,999... = 1 está íntimamente relacionada con la ausencia de números reales infinitesimales no nulos. Algunos sistemas de numeración alternativos, como los números hiperreales, sí contienen infinitesimales no nulos; en estos sistemas, a diferencia de los reales, puede haber números cuya diferencia con el 1 sea menor que cualquier número racional. Otros sistemas, como por ejemplo los números p-ádicos, tienen otra forma de «expansión decimal», que se comporta de manera muy distinta a la expansión de los números reales. Aunque los números reales son el objeto de estudio más común en el campo del análisis matemático, tanto los hiperreales como los p-ádicos tienen aplicaciones en esta área.
Demostraciones algebraicas
Fracciones y división euclidiana
Una razón por la que los decimales infinitos son una ampliación necesaria de los decimales finitos, es que permite la representación de fracciones. Utilizando el algoritmo de la división, una simple división de enteros como 1/9, se convierte en el decimal periódico 0,111..., en el que los dígitos se repiten sin fin. Este ejemplo se utiliza para dar una rápida demostración de que 0,999... = 1.
La multiplicación de 9 por 1 da 9 en cada dígito, así 9 × 0,111... = 0,999..., y 9 × 1/9 = 1, lo que implica que 0,999... = 1:[2]
Una alternativa, también muy frecuente, es utilizar 1/3 = 0,333... y multiplicar por 3.
Multiplicación por 10
Cuando un número escrito en notación decimal se multiplica por 10, los dígitos no cambian pero el separador decimal se mueve un lugar a la derecha. Así, 10 × 0,999... = 9,999..., que es 9 unidades mayor que el número original. Para comprobarlo, basta restar 0,999... de 9,999..., los dígitos a la derecha del separador decimal se cancelan uno a uno, y el resultado es 9 − 9 = 0 para cada uno de estos dígitos:
Discusión
Aunque estas pruebas demuestran que 0,999... = 1, el pretender que «explican» la ecuación, depende de las expectativas de la audiencia atendida. En aritmética elemental, estas pruebas ayudan a explicar por qué 0,999... = 1, o por qué 0,333... < 0,34. En álgebra elemental, estas demostraciones explican por qué el método general de conversión entre fracciones y números decimales funciona. Pero las pruebas no aclaran la relación fundamental entre los decimales y los números a los cuales representan, donde subyace la pregunta de cómo dos decimales distintos pueden ser, de hecho, iguales.[3] William Byers argumenta que el estudiante que acepta que 0,999... = 1 basado en estas pruebas, pero que no ha resuelto la ambigüedad, no ha entendido realmente la ecuación.[4] Según Fred Richman, el primer argumento «toma su fuerza del hecho de que la mayor parte de la gente ha sido adoctrinada para aceptar la primera ecuación sin pensarlo».[5]
Una vez que se ha definido un esquema representativo, se puede utilizar para justificar las reglas de la aritmética decimal utilizada en estas demostraciones. Más aún, se puede demostrar directamente que los decimales 0,999... y 1,000... representan el mismo número real; esta construcción por definición se explica más abajo.
Demostraciones analíticas
Como la cuestión de 0,999... no afecta al desarrollo formal de las matemáticas, se puede aplazar hasta que se demuestren los teoremas estándares del análisis real. Un requisito es caracterizar los números reales que se pueden escribir en notación decimal, compuesto por un signo opcional, una secuencia finita de cualquier número de dígitos que forman la parte entera, un separador decimal y una secuencia de dígitos que forman la parte fraccionaria. Para hablar de 0,999... la parte entera se puede resumir como b0 y se pueden descuidar negativos, así una expansión decimal tiene la forma
Es vital que la parte fraccionaria, a diferencia de la parte entera, no esté limitada a un número finito de dígitos. Esto es una notación posicional, así por ejemplo, el cinco en 500 contribuye diez veces más que el 5 en 50, y el 5 en 0,05 contribuye una décima parte del 5 en 0,5.
Series infinitas y sucesiones
El desarrollo quizá más común de las expansiones decimales, es definirlas en términos de series infinitas. En general:
Para 0,999... se puede aplicar el teorema de convergencia de las series geométricas:[6]
- Si entonces
Dado que 0,999... es una suma de este tipo, con , el teorema resuelve rápidamente la cuestión:
Esta demostración (de hecho, que 10 es igual a 9,999...) aparece ya en 1770 en Elementos de álgebra de Leonhard Euler.[7]
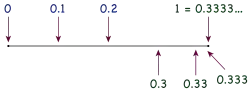
La suma de series geométricas en sí, son un resultado anterior a Euler. Una demostración típica del siglo XVIII utiliza una manipulación término-a-término similar a la demostración algebraica antes expuesta; en 1811, el libro de texto de Bonnycastle Una Introducción al Álgebra utiliza una serie geométrica de este tipo para justificar la misma maniobra sobre 0,999....[8] Una reacción del siglo XIX contra tales métodos de adición liberales resultó en la definición que aún domina hoy: la suma de una serie se define como el límite de la sucesión de sus sumas parciales. Una demostración correspondiente del teorema calcula explícitamente esta sucesión; se puede encontrar en cualquier introducción al cálculo o el análisis basado en la demostración.[9]
Una sucesión (x0, x1, x2, ...) tiene por límite x si la distancia |x − xn| se vuelve arbitrariamente pequeña a medida que n aumenta. La afirmación misma 0,999... = 1 puede ser interpretada y demostrada como límite:[10]
El último paso, que , suele justificarse por el axioma de la propiedad arquimediana de los números reales. Esta actitud hacia basada en límites es por cierto más evocadora, aunque mucho menos precisa. Por ejemplo, en el libro de texto de 1846 The University Arithmetic se explica: «0,999 +, continuando al infinito = 1, porque cada 9 anexado acerca el valor aún más a 1»; el texto de 1895 Arithmetic for Schools dice «...cuando se toma una gran cantidad de 9s, la diferencia entre 1 y 0,99999... se vuelve inconcebiblemente pequeña».[11] Tales enfoques heurísticos suelen ser interpretados por los estudiantes como que 0,999... en sí es menor que 1.
Intervalos encajados y cotas superiores
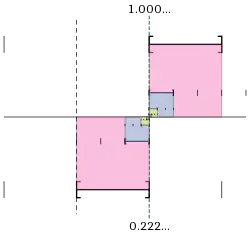
La definición de series expuesta más arriba es una manera sencilla de definir un número real denotado por una expansión decimal. El proceso opuesto proporciona una visión complementaria: para un número real dado, definir la expansión decimal que lo denota.
Si un número real x pertenece al intervalo cerrado [0 ; 10] (i.e, es mayor o igual a cero y menor o igual a diez), se puede dividir este intervalo en diez partes que se superpongan únicamente en las extremidades: [0 ; 1], [1 ; 2], [2 ; 3], y así hasta [9 ; 10]. El número x debe pertenecer a alguno de ellos; si pertenece a [2 ;3], se anota el dígito «2» y se subdivide ese intervalo en [2 ; 2,1], [2,1 ; 2,2], ..., [2,8 ; 2,9], [2,9 ; 3]. Continuando este proceso se obtiene una sucesión infinita de intervalos encajados, rotulados por una sucesión infinita de dígitos b0, b1, b2, b3, ..., que se escriben
Con este formalismo, las identidades 1 = 0,999... y 1 = 1,000... reflejan, respectivamente, el hecho de que el 1 esté tanto en el intervalo [0 ; 1] como en [1 ; 2], por lo que se puede elegir cualquiera de los dos intervalos al escribir los dígitos. Para asegurarse de que esta notación no abuse del signo «=», se requiere de un método que permita reconstruir un único número real para cada decimal, como por ejemplo los límites; otras construcciones abordan el tema del ordenamiento.[12]
Una opción directa es el teorema de los intervalos encajados, que garantiza que, dada una sucesión de intervalos cerrados encajados, cuya longitud se puede hacer arbitrariamente pequeña, los intervalos contienen exactamente un número real en su intersección. Así, b0,b1b2b3... queda definido como el único número contenido en todos los intervalos [b0 ; b0 + 1], [b0,b1 ; b0,b1 + 0,1], y así sucesivamente. De este modo, 0,999... es el único número real que está en todos los intervalos [0 ; 1], [0,9 ; 1], [0,99 ; 1], y [0,99...9 ; 1] para cada cola finita de 9s. Puesto que el 1 es un elemento de cada uno de estos intervalos, 0,999... = 1.[13]
El teorema de los intervalos surge por lo general como una característica aún más fundamental de los números reales: la existencia de la mínima cota superior o supremo. Para explotar directamente estos objetos, se define b0,b1b2b3... como la mínima cota superior del conjunto de aproximantes {b0 ; b0,b1 ; b0,b1b2 ; ...}.[14] Se puede demostrar que esta definición (o la definición de los intervalos encajados) es consistente con el proceso de subdivisión, lo cual implica 0,999... = 1 nuevamente. Tom Apostol concluye,
El hecho de que un número real pueda tener dos representaciones decimales diferentes es meramente un reflejo del hecho de que dos conjuntos diferentes de números reales pueden tener el mismo supremo.[15]
Demostraciones por construcción de los números reales
Se puede definir explícitamente a los números reales como una cierta estructura construida sobre los números racionales, basándose en la teoría axiomática de conjuntos. Los números naturales – 0, 1, 2, 3, ... – comienzan en 0 y continúan ascendentemente, de modo que cada número tiene un sucesor. Este conjunto se puede extender al añadírsele los negativos, obteniéndose así el conjunto de los números enteros; éstos, a su vez, también se pueden extender, si se añaden los cocientes, a los números racionales. Estos conjuntos numéricos se acompañan de las cuatro operaciones aritméticas fundamentales: suma, resta, multiplicación y división. De manera más sutil, poseen un ordenamiento, de modo que cada uno de estos números puede ser comparado con algún otro, y será menor que, mayor que, o igual a este otro número.
El paso de los racionales a los reales es una extensión mucho mayor. Hay al menos dos maneras corrientes de hacerlo, ambas publicadas en 1872: por medio de las cortaduras de Dedekind y por sucesiones de Cauchy. Pruebas de que 0,999... = 1 que utilicen directamente estas construcciones no se encuentran en libros de texto de análisis real, donde la tendencia moderna durante las últimas décadas ha sido el uso del análisis axiomático. Incluso cuando la hay, la construcción es usualmente aplicada a la demostración de los axiomas de los números reales, que luego apoyan las pruebas anteriores. No obstante, muchos autores sostienen que comenzar con la construcción es más apropiado lógicamente, y las pruebas que resultan tienen mayor autonomía.[16]
Cortaduras de Dedekind
En el método de las cortaduras de Dedekind, cada número real x se define como el conjunto infinito de todos los números racionales que son menores que x.[17] En particular, el número real 1 es el conjunto de todos los números racionales menores a 1.[18] Toda expansión decimal positiva determina fácilmente una cortadura de Dedekind: el conjunto de números racionales que son menores que alguna etapa de la expansión. Luego el número real 0,999... es el conjunto de números racionales r tales que r < 0, o r < 0,9, o r < 0,99, o r es menor que algún otro número de la forma
- .[19]
Todo elemento de 0,999... es menor que 1, luego es un elemento del número real 1. Inversamente, un elemento de 1 es un número racional
lo cual implica
Dado que 0,999... y 1 contienen los mismos números racionales, son el mismo conjunto: 0,999... = 1.
Esta definición de los números reales como cortaduras de Dedekind fue publicada por primera vez por Richard Dedekind en 1872.[20] El método descrito anteriormente para asignar un número real a cada expansión decimal es debido a una publicación de carácter explicativo intitulada: "Is 0.999 ... = 1?" de Fred Richman en Mathematics Magazine, dirigida a enseñantes de matemática de nivel intermedio y sus estudiantes.[21] Richman nota que al tomar las cortaduras de Dedekind en cualquier subconjunto denso de los números racionales se obtiene el mismo resultado; en particular, utiliza fracciones decimales, para las cuales la demostración es más inmediata. También nota que, típicamente, las definiciones permiten que { x : x < 1 } sea una cortadura pero no { x : x ≤ 1 } (o viceversa).
"¿Para qué hacer esto? Precisamente para eliminar la posibilidad de que existan números distintos 0,9* y 1. [...] Entonces vemos que en la definición tradicional de los números reales, la ecuación 0,9* = 1 está incorporada desde el comienzo."[22] Una modificación suplementaria del proceso lleva a una estructura diferente en donde no son iguales. Aunque consistente, muchas de las operaciones aritméticas usuales fallan, por ejemplo la fracción 1/3 no tiene representación; véase sistemas de numeración alternativos más abajo.
Sucesiones de Cauchy
Otro método de construcción de los números reales utiliza el ordenamiento de los racionales de manera menos directa. Se define primero la distancia entre x e y como el valor absoluto |x − y|, donde el valor absoluto |z| se define como el máximo entre z y −z, por lo que nunca es negativo. Se define entonces a los números reales como la sucesión de racionales que cumplen la propiedad de las sucesiones de Cauchy con esta distancia, esto es: en la sucesión (x0, x1, x2, ...), una aplicación de los números naturales en los racionales, para todo racional positivo δ existe N tal que |xm − xn| ≤ δ para todo m, n > N (la distancia entre los términos se vuelve menor que cualquier número racional positivo).[23]
Si (xn) y (yn) son dos sucesiones de Cauchy, entonces se definen como números reales iguales si la sucesión (xn − yn) tiene por límite 0. Truncamientos del número decimal b0,b1b2b3... generan una sucesión de racionales que es de Cauchy; de esta manera se define el valor real del número.[24] Luego, según este formalismo, la tarea es mostrar que la sucesión de números racionales
tiene por límite 0. Considerando el n-ésimo término de la sucesión, para n=0,1,2,..., se debe mostrar entonces que
Este límite se calcula fácilmente;[25] una demostración posible es la siguiente: para ε = a/b > 0 se puede tomar N = b en la definición de límite de una sucesión. Así, nuevamente 0,999... = 1.
La definición de los números reales como sucesiones de Cauchy fue publicada por primera vez de manera independiente por Eduard Heine y Georg Cantor, también en 1872.[20] El método de las expansiones decimales descrito anteriormente, incluyendo la prueba de que 0,999... = 1, sigue de cerca el trabajo de Griffiths & Hilton de 1970 "Un libro de texto comprensible de matemática clásica: una interpretación contemporánea". El libro está escrito específicamente para ofrecer una segunda mirada sobre conceptos familiares bajo una interpretación moderna.[26]
Generalizaciones
El resultado 0,999... = 1 se generaliza rápidamente de dos formas. En primer lugar, todo número no nulo con una notación decimal finita (equivalentemente, con una sucesión infinita de ceros) tiene un homólogo con infinitos nueves, por ejemplo: 0,24999... es igual a 0,25 exactamente como en el caso especial considerado. Estos números son exactamente las fracciones decimales, y son densas.[27]
En segundo lugar, un teorema comparable puede aplicarse en cada radix o base, por ejemplo: en base 2 (sistema binario), 0,111... es igual a 1, y en base 3 (sistema ternario), 0,222... es igual a 1. Los libros de texto de análisis real suelen obviar el ejemplo 0,999... y presentan alguna de estas dos generalizaciones desde el comienzo.[28]
Representaciones alternativas del 1 también se dan en bases no enteras, por ejemplo, en la base áurea, las dos representaciones estándar son 1,000... y 0,101010..., y existen infinitas representaciones más que incluyen 1s adyacentes. En general, para casi todo q entre 1 y 2, existen incontables expansiones en q-base del 1. Por otro lado, hay incontables q (incluyendo todos los números naturales mayores que 1) para los cuales solo hay una expansión en q-base del 1, además del 1,000.... trivial. Este resultado fue obtenido por vez primera por Paul Erdős, Miklos Horváth e István Joó alrededor de 1990. En 1998, Vilmos Komornik y Paola Loreti determinaron la menor base de este tipo, la constante de Komornik–Loreti q = 1,787231650.... En esta base, 1 = 0,11010011001011010010110011010011...; los dígitos vienen dados por la sucesión de Thue-Morse, que no se repite.[29]
Una generalización de mayor alcance hace referencia a los sistemas de numeración posicional más generales. Estos sistemas también tienen múltiples representaciones, y, en cierto sentido, revisten mayor complicación, por ejemplo:[30]
- En el sistema ternario balanceado, 1/2 = 0,111... = 1,111....
- En el inverso del sistema factorádico (utilizando bases 2,3,4,... para posiciones después del punto decimal), 1 = 1,000... = 0,1234....
Imposibilidad de la representación única
El hecho de que todos estos sistemas de numeración distintos provean múltiples representaciones para algunos números reales, se puede atribuir a una diferencia fundamental entre los números reales, en tanto que conjunto ordenado, y una colección de cadenas infinitas de símbolos ordenados lexicográficamente. De hecho, las siguientes dos propiedades dan cuenta de esta dificultad:
- Si un intervalo de los números reales se particiona en dos partes no vacías L y R tales que cada elemento de L sea (estrictamente) menor que todo elemento de R, entonces: o bien L contiene un elemento mayor, o bien R contiene un elemento menor, pero no ambos.
- La colección de cadenas infinitas de símbolos tomados de cualquier «alfabeto» finito, ordenado lexicográficamente, puede ser particionado en dos partes no vacías L y R, tales que cada elemento de L es menor que todo elemento de R, donde L contiene un elemento mayor y R contiene un elemento menor. De hecho, es suficiente con tomar dos subcadenas finitas (iniciales) p1, p2 de elementos de la colección, tales que difieran únicamente en el símbolo final, para el cual tienen valores sucesivos, y tomar para L el conjunto de todas las cadenas en la colección cuya subcadena correspondiente sea a lo más p1, y para el residuo R, la cadena de la colección cuya subcadena correspondiente sea al menos p2. Luego, L tiene un elemento mayor, comenzando por p1 y eligiendo el mayor símbolo disponible en todas las posiciones siguientes, donde R tiene un elemento menor que se obtiene al seguir p2 del menor símbolo en todas las posiciones.
El primer punto se deduce de propiedades básicas de los números reales: L tiene un supremo, R tiene un ínfimo, y se ve inmediatamente que son iguales; un número real estará en R o en L pero no en ambos, pues son conjuntos disjuntos. El segundo punto generaliza el par 0,999.../1,000... obtenido por p1 = "0", p2 = "1". De hecho, no es necesario utilizar el mismo alfabeto para todas las posiciones (de modo que por ejemplo los sistemas de raíz mixta pueden ser incluidos) o considerar la colección completa de cadenas posibles; los únicos puntos importantes son que, en cada posición, un conjunto finito de símbolos (que pueden depender incluso de los símbolos previos) pueda ser escogido (esto es necesario para asegurar elecciones máximas y mínimas), y que al hacer una elección válida para cualquier posición, el resultado debe ser una cadena infinita válida (de modo que no se permite «9» en cada posición si se prohíben sucesiones infinitas de «9»s). Bajo estas premisas, el argumento anterior muestra que una aplicación que preserva el orden de la colección de cadenas a un intervalo de números reales, no puede ser una biyección: o bien algunos números no corresponden a ninguna cadena, o bien algunos de ellos corresponden a más de una cadena.
Marko Petkovšek demostró que para todo sistema posicional que nombre a todos los números reales, el conjunto de reales que tendrá representación múltiple es siempre denso. Llama a esta demostración: «un ejercicio instructivo en topología punto-conjunto»; involucra conjuntos de valores posicionales vistos como espacios de Stone y el hecho de que su representación real viene dada por funciones continuas.[31]
Aplicaciones
Una aplicación de 0,999... como representación de 1 se da en teoría de números elemental. En 1802, H. Goodwin publicó una observación sobre la aparición de 9s en las representaciones decimales periódicas de fracciones cuyo denominador son ciertos números primos. Por ejemplo
- 1/7 = 0,142857142857... y 142 + 857 = 999.
- 1/73 = 0,0136986301369863... y 0136 + 9863 = 9999.
E. Midy probó un resultado general sobre estas fracciones, hoy llamado el teorema de Midy, en 1836. La prueba es oscura, y no está claro si su demostración involucra directamente 0,999..., pero hay al menos una prueba moderna, realizada por W. G. Leavitt, que sí lo hace; si se puede demostrar que un número decimal de la forma 0.b1b2b3... es un entero positivo, entonces tiene que ser 0,999..., que es la fuente de los 9s en el teorema.[32] Las investigaciones en esta dirección pueden motivar el desarrollo de conceptos tales como máximo común divisor, aritmética modular, números de Fermat, orden de elementos de un grupo y la ley de reciprocidad cuadrática.[33]
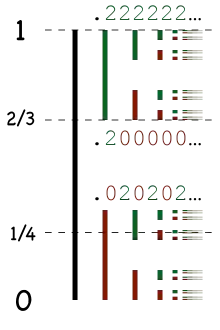
En análisis real, el caso análogo en base-3: 0,222... = 1, juega un papel esencial en la caracterización de uno de los fractales más simples: el conjunto de Cantor:
- Un punto del intervalo unidad está en el conjunto de Cantor si y solo si puede ser representado en sistema ternario utilizando únicamente los dígitos 0 y 2.
El n-ésimo dígito de la representación refleja la posición del punto en la n-ésima etapa de la construcción. Por ejemplo, el punto 2⁄3 se da con la representación usual de 0,2 o 0,2000..., dado que está a la derecha de la primera etapa y a la izquierda de toda etapa de construcción posterior. El punto 1⁄3 se representa no como 0,1 sino como 0,0222..., pues está a la izquierda de la primera etapa y a la derecha de toda etapa de construcción posterior.[34]
Los nueves repetidos aparecen también en otro trabajo de George Cantor: deben tomarse en cuenta para construir una prueba válida, al aplicar su prueba diagonal de 1891 a las expansiones decimales ed la no denombrabilidad del intervalo unidad. Esta demostración necesita poder declarar la diferencia entre ciertos pares de números reales basada en sus expansiones decimales, por lo que se deben evitar parejas como 0,2 y 0,1999... Un método simple representa todos los números con expansión no finita; el método opuesto excluye nueves repetitivos.[35] Una variante quizá más cercana al argumento original de Cantor utiliza de hecho base-2: transformando las expansiones en base-3 en expansiones en base-2, se puede demostrar igualmente la no denombrabilidad del conjunto de Cantor.[36]
Escepticismo en la enseñanza
Los estudiantes en matemática suelen rechazar la igualdad de 0,999... y 1, por razones que van desde su apariencia dispar, hasta profundos equívocos sobre el concepto de límite de una sucesión y la naturaleza de los infinitesimales. Hay varios factores que contribuyen a la confusión:
- Los estudiantes suelen estar «mentalmente comprometidos con la noción de que un número se puede representar de una manera y solo de una manera por un decimal.» Ver dos decimales manifiestamente distintos representando el mismo número parece una paradoja, lo cual se amplifica por la apariencia del supuestamente bien entendido número 1.[37]
- Algunos estudiantes interpretan «0,999...» (o alguna notación similar) como una cola larga pero finita de 9s, posiblemente con una longitud variable y no especificada. Si aceptan una cola infinita de nueves, pueden esperar aún un último 9 «al infinito».[38]
- La intuición y la enseñanza ambigua llevan a los estudiantes a pensar que el límite de una sucesión es algún tipo de proceso infinito en lugar de un valor fijo, dado que una sucesión no necesariamente alcanza su límite. Cuando los estudiantes aceptan la diferencia entre una sucesión de números y su límite, pueden llegar a leer «0,999...» como si significara la sucesión en lugar de su límite.[39]
Estas ideas suelen malinterpretarse en el contexto tradicional de los números reales, aunque algunas de ellas pueden ser válidas en otros sistemas de numeración, ya sea inventados por su utilidad matemática en general, o como contraejemplos instructivos para una mejor comprensión de 0,999...
Muchas de estas explicaciones han sido propuestas por el profesor David O. Tall, quien ha estudiado las características de la enseñanza y la cognición que llevan a algunos de los malentendidos que ha encontrado entre sus estudiantes del colegio. Interrogando a sus estudiantes para determinar por qué la vasta mayoría rechaza inicialmente la igualdad, encontró que «los estudiantes continúan concibiendo el 0,999... como una sucesión de números que se acercan más y más a 1 y no como un valor fijo, porque 'no se ha especificado cuántos lugares hay' o 'es el decimal más cercano posible debajo del 1'».[40]
De las pruebas elementales, multiplicar 0,333... = 1⁄3 por 3 es aparentemente una estrategia convincente para persuadir a los estudiantes reticentes de que 0,999... = 1. Aun así, confrontados con el conflicto entre su creencia en la primera ecuación y la negación acerca de la segunda, algunos estudiantes comienzan a descreer de la primera, o bien, terminan frustrados.[41] Tampoco están a salvo métodos más sofisticados: estudiantes que son absolutamente capaces de aplicar definiciones rigurosas, pueden aún sentir la necesidad de recurrir a imágenes intuitivas cuando son sorprendidos por resultados matemáticos avanzados, incluyendo 0,999... Por ejemplo, en análisis real, una estudiante fue capaz de probar que 0,333... = 1⁄3 utilizando la definición del supremo, para luego insistir en que 0,999... < 1 basada en su conocimiento previo de división euclídea.[42] Algunos más, son capaces de probar que 1⁄3 = 0,333..., pero, confrontados con la prueba por fracciones, insisten en que la «lógica» prevalece sobre los cálculos matemáticos.
Joseph Mazur cuenta la historia de un brillante estudiante suyo de cálculo que «cuestionaba casi todo lo que yo decía en clase pero nunca cuestionaba su calculadora,» y que creía que nueve dígitos era todo lo que se necesitaba para hacer matemáticas, incluyendo el cálculo de la raíz cuadrada de 23; este estudiante quedó inconforme con el argumento de que 9,99... = 10, llamándolo un «feroz proceso imaginativo de crecimiento infinito»."[43]
Como parte de la teoría APOS de Ed Dubinsky del aprendizaje matemático, Dubinsky y sus colaboradores (2005) proponen que aquellos estudiantes que conciben el 0,999... como una cola finita indeterminada, a una distancia infinitamente pequeña del 1, «no han construido aún un proceso de concepción completo del decimal infinito». Otros estudiantes que han completado la concepción del proceso de 0,999... quizá no han sido aún capaces de «encapsular» ese proceso dentro de una «concepción del objeto», como la concepción que tienen del objeto 1, y por esto ven el proceso 0,999... y del objeto 1 como incompatibles. Dubinsky et al. también relacionan esta habilidad mental de encapsulación con ver 1⁄3 como un número con derecho propio y con tratar al conjunto de números naturales como un todo.[44]
En la cultura popular
Con el auge de Internet, los debates acerca del 0,999... han traspasado los salones de clases y son lugar común en grupos de noticias y foros, incluyendo varios que de hecho tienen poco que ver con las matemáticas. En el grupo de noticias sci.math, argumentar sobre 0,999... es un «deporte popular», y es una de las preguntas que se responden en sus FAQ (preguntas frecuentes).[45] Las FAQ abarcan brevemente el caso 1⁄3, multiplicación por 10, límites y también alude a las sucesiones de Cauchy.
La edición del 2003 de la columna «interés general» del diario The Straight Dope discute 0,999... vía 1⁄3 y límites, y habla de los malentendidos surgidos en el tema:
El primate inferior que nos habita aún se resiste, diciendo: 0,999~ no representa verdaderamente un número, sino, un proceso. Para encontrar un número debemos parar el proceso, punto en que la igualdad 0,999~ = 1 se rompe. Es cualquier cosa.[46]
La crónica The Straight Dope cita una discusión en su propio foro, traído de «otro foro anónimo que trata principalmente de... juegos de video». En la misma vena, la cuestión del 0,999... tuvo tanto éxito durante los primeros siete años del foro Battle.net de la sociedad Blizzard Entertainment, que la compañía emitió un comunicado el 1° de abril de 2004 (día del pescado de abril), afirmando que, definitivamente, es 1:
Estamos muy emocionados por cerrar este libro de discusiones de una vez por todas. Hemos sido testigos de la aprehensión y preocupación de nuestros clientes por saber si 0,999~ es o no igual a 1, y estamos orgullosos de anunciar que la siguiente demostración, finalmente, y de manera concluyente, resuelve el tema.[47]
Dos pruebas siguen a continuación, basadas en límites y en la multiplicación por 10.
0,999... es también parte del folklore matemático:[48]
Pregunta: ¿Cuántos matemáticos se necesitan para cambiar un foco? Respuesta: 0,999999...
En sistemas de numeración alternativos
Si bien los números reales forman un sistema de numeración extremadamente útil, la decisión de interpretar que la notación «0,999...» denota un número real es, en última instancia, una convención; Timothy Gowers arguye, en ''Mathematics: A Very Short Introduction, que la identidad resultante 0,999... = 1 es igualmente una convención:
En todo caso, no es en absoluto una convención arbitraria, puesto que el no adoptarla lo fuerza a uno a inventar nuevos objetos extraños o a abandonar algunas de las reglas familiares de la aritmética.[49]
Es posible definir otros sistemas de numeración utilizando diferentes reglas u objetos nuevos; en algunos de estos sistemas, las demostraciones anteriores tendrían que ser reinterpretadas y se podría encontrar que, en un sistema de numeración dado, 0,9... y 1 podrían no ser idénticos. En todo caso, muchos sistemas de numeración son extensiones del – más que alternativas independientes al – sistema de números reales, por lo que 0,999... = 1 sigue siendo cierto. Incluso en dichos sistemas de numeración, vale la pena examinar sistemas de numeración alternativos, no solo por cómo 0,999... se comporta (si, para el caso, un número expresado como «0,999...» tuviese sentido y no fuese ambiguo), sino también por el comportamiento de fenómenos relacionados. Si alguno de estos fenómenos difiere de aquellos que se presentan en el sistema de los números reales, entonces al menos alguna de las hipótesis de base del nuevo sistema debe ser falso.
Infinitesimales
Algunas de las demostraciones de que 0,999... = 1 se basan en la propiedad arquimediana de los números reales: no hay infinitesimales no nulos. Específicamente, la diferencia 1 − 0,999... debe ser menor que cualquier número racional positivo, por lo que debe ser un infinitesimal; dado que los números reales no contienen infinitesimales no nulos, se sigue que la diferencia debe ser cero, y por lo tanto los dos valores son el mismo.
Se pueden construir estructuras algebraicas ordenadas, matemáticamente coherentes, incluyendo varias alternativas a los números reales, que son no arquimedianas. Por ejemplo, los números duales incluyen un nuevo elemento infinitesimal ε, análogo a la unidad imaginaria i de los números complejos, excepto por el hecho que ε2 = 0. La estructura que resulta es de utilidad en diferenciación automática. Los números duales se pueden dotar de un orden lexicográfico, en cuyo caso los múltiplos de ε se convierten en elementos no arquimedianos.[50] Hay que notar que, no obstante, en tanto que extensión de los números reales, los números duales aún conllevan 0,999... = 1. Hay que notar además que, si bien ε existe en los números duales, también ε/2, por lo que ε no es «el menor número dual positivo», y, de hecho, como en los reales, no existe tal elemento.
El análisis no estándar provee un sistema de numeración con todo un conjunto de infinitesimales (y sus inversos).[51] A. H. Lightstone desarrolla una expansión decimal para los números hiperreales en (0 ; 1)∗.[52] Lightstone muestra cómo asociar a cada número una sucesión de dígitos,
indexados por los números hipernaturales. Aunque no discute directamente 0,999..., muestra que el número real 1/3 se representa por 0,333...;...333... como consecuencia del principio de transferencia. En particular, «0,333...;...000...» y «0,999...;...000...» no corresponden a ningún número.
Al mismo tiempo, el número hiperrreal con el último dígito 9 a un rango infinito hipernatural H, satisface la desigualdad estricta . Subsecuentemente, Karin Katz y Mikhail Katz proponen una evaluación alternativa de «0,999...»:
Todas estas interpretaciones sitúan «0,999...» infinitamente cerca del 1. Ian Stewart caracteriza esta interpretación como una forma «absolutamente razonable» de justificar rigurosamente la intuición de que «falta algo muy pequeño» entre 0,999... y 1....[54] Junto con Katz & Katz, Robert Ely también cuestiona la suposición de que las ideas de los estudiantes sobre el hecho de que provengan de intuiciones erróneas acerca de los números reales, y las interpreta como intuiciones «no estándar» que pueden ser preciadas dentro del aprendizaje del cálculo.[55][56]
Hackenbush
La teoría de juegos combinatorios provee números alternativos a los reales; un ejemplo notorio es el Hackenbush[57] azul-negro infinito. En 1974, Elwyn Berlekamp describió la correspondencia entre las cadenas Hackenbush y la expansión binaria de los números reales, motivado por la idea de la compresión de datos. En este ejemplo, el valor de la cadena Hackenbush LRRLRLRL... es 0.0101012... = 1/3, sin embargo, el valor de LRLLL... (correspondiente a 0.111...2) es infinitesimalmente menor que 1. La diferencia entre los dos es el número surreal 1/ω, donde ω es el primer número ordinal infinito; la representación correspondiente es LRRRR... o 0.000...2.[58]
Esto se da de hecho en la expansión binaria de muchos números racionales, donde el valor de los números es el mismo pero el árbol de los caminos binarias correspondientes son distintas. Por ejemplo, 0.10111...2 = 0.11000...2, son ambas iguales a 3/4, pero la primera representación corresponde al árbol del camino binario LRLRRR... mientras que la segunda corresponde al otro camino LRRLLL....
Sustracción no definida
En los casos en que la operación de sustracción no esté definida, entonces 1 − 0,999... simplemente no existe, y las pruebas dadas más arriba dejan de ser válidas. Estructuras matemáticas en que la operación aditiva está definida pero no la operación de sustracción incluyen, por ejemplo, semigrupos conmutativos, monoides conmutativos y semianillos. Richman considera dos de estos sistemas, diseñados de manera tal que 0,999... < 1.
En primer lugar, Richman define un número decimal no negativo como una expansión decimal literal. Define el orden lexicográfico y la operación de adición, notando que 0,999... < 1 simplemente porque 0 < 1 en el lugar de las unidades, pero para cualquier x no terminal, se tiene 0,999... + x = 1 + x. Luego, una peculiaridad de los números decimales, es que la adición no siempre se puede cancelar; otra es que ningún número decimal corresponde a 1⁄3. Después de definir la multiplicación, los números decimales forman un semianillo conmutativo positivo, totalmente ordenado.[59]
En el proceso de definir la multiplicación, Richman también define otro sistema al que llama «corte D», que es el conjunto de cortaduras de Dedekind de las fracciones decimales. Ordinariamente, esta definición lleva a los números reales, pero para una fracción decimal d, Richman la altera ligeramente permitiendo tanto el corte (−∞, d ) como el corte (−∞, d ], al que llama «corte principal». El resultado es que no hay infinitesimales positivos en las cortaduras D, pero hay «un tipo de infinitesimal negativo» 0− que no posee expansión decimal.
Richman concluye que 0,999... = 1 + 0−, mientras que la ecuación «0,999... + x = 1» no tiene solución.[60]
Números p-ádicos
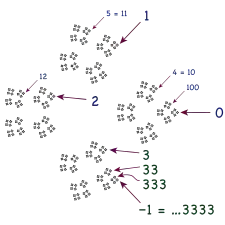
El 10-ádico análogo es ...999 = −1.
Al ser interrogados acerca de 0,999..., los novatos a menudo piensan que debe haber un «9 final», creen que 1 − 0,999... es un número positivo que pueden escribir como «0,000...1». Tenga o no tenga esto sentido, el objetivo intuitivo es claro: sumar 1 al último 9 en 0,999... acarrea todos los 9's a 0's y deja 1 en el lugar de las unidades. Entre otras razones, esta idea falla pues no hay un «último 9» en 0,999...[61] Sin embargo, existe un sistema que contiene una cola infinita de 9's incluyendo un último 9.
Los números p-ádicos es un sistema de numeración alternativo de interés en teoría de números. Como los números reales, los números p-ádicos pueden construirse a partir de los números racionales vía sucesiones de Cauchy; la construcción utiliza una métrica diferente en la cual 0 está más cerca de p, y mucho más cerca de pn que de 1. Los números p-ádicos forman un campo para p primo y un anillo para otro p, incluyendo el 10. Luego, la aritmética es posible en los p-ádicos, y no hay infinitesimales.
En los números 10-ádicos, los análogos de las expansiones decimales corren hacia la izquierda. La expansión 10-ádica ...999 tiene un último 9, y no tiene un primer 9. Se puede sumar un 1 al lugar de las unidades, lo que deja detrás solo 0's después del acarreo: 1 + ...999 = ...000 = 0, y así ...999 = −1.[62] Otra derivación utiliza series geométricas. La serie infinita multiplicada por «...999» no converge en los números reales, pero converge en los 10-ádicos, lo que permite reutilizar la fórmula familiar:
Una tercera derivación fue inventada por una estudiante desconfiada del argumento de su profesor basado en límites, para probar que 0,999... = 1; se inspiró de la prueba multiplicación por 10 en la dirección opuesta: si x = ...999 entonces 10x = ...990, luego 10x = x − 9, por lo que x = −1 nuevamente.[62]
Como última extensión, dado que 0,999... = 1 (en los reales) y ...999 = −1 (en los 10-ádicos), entonces con «fe ciega y manipulación descarada de símbolos»[64] uno puede sumar las dos ecuaciones y llegar a ...999,999... = 0. Esta ecuación no tiene sentido ni como expansión 10-ádica ni como expansión decimal ordinaria, pero resulta ser significativa y verdadera si se desarrolla una teoría de «dobles-decimales» con, eventualmente, terminaciones repetitivas a la izquierda para representar un sistema muy conocido: los números reales.[65]
Véase también
Fuentes
Referencias
- 0,9 periódico también se puede escribir como o o o bien como un seguido de tantos 9's como se desee en la parte decimal periódica.
- Peressini p.186.
- Este argumento se encuentra en Peressini y Peressini p. 186.
- Byers pp. 39–41.
- Richman p. 396.
- Rudin p. 61, Theorem 3.26; J. Stewart p. 706
- Euler p.170.
- Grattan-Guinness p.69; Bonnycastle p.177.
- J. Stewart p.706, Rudin p.61, Protter y Morrey p.213, Pugh p.180, J.B. Conway p.31.
- El límite sigue, por ejemplo, de Rudin p. 57, Teorema 3.20e. Para un enfoque más directo, ver también Finney, Weir, Giordano (2001) Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Sección 8.1, ejemplo 2(a), ejemplo 6(b).
- Davies p. 175; Smith y Harrington p. 115.
- Beals p. 22; I. Stewart p. 34.
- Bartle and Sherbert pp. 60–62; Pedrick p. 29; Sohrab p. 46.
- Apostol pp. 9, 11–12; Beals p. 22; Rosenlicht p. 27.
- Apostol p. 12.
- La síntesis histórica fue reivindicada por Griffiths y Hilton (p.xiv) en 1970 y de nuevo por Pugh (p. 10) en 2001; ambos prefieren de hecho las cortaduras de Dedekind a los axiomas. Para el uso de las cortaduras en libros de texto, véase Pugh p. 17 o Rudin p. 17. Para puntos de vista en lógica, Pugh p. 10, Rudin p.ix, o Munkres p. 30.
- Enderton (p. 113) dice al respecto: «La idea detrás de las cortaduras de Dedekind es que un número real x puede denotarse por medio de un conjunto infinito de racionales, netamente, todos los racionales menores que x. Definiremos en efecto a x como el conjunto de racionales menores que x. Para evitar circularidad en la definición, debemos poder caracterizar los conjuntos de racionales que pueden obtenerse de esta forma...»
- Rudin pp. 17–20, Richman p. 399, o Enderton p. 119. Para ser precisos, Rudin, Richman, y Enderton llaman a esta cortadura 1*, 1−, y 1R, respectivamente; los tres la identifican con el número real 1 tradicional. Nótese que lo que Rudin y Enderton llaman una cortadura de Dedekind, Richman lo llama «cortadura no principal de Dedekind».
- Richman p. 399.
- J J O'Connor and E F Robertson (octubre de 2005). «History topic: The real numbers: Stevin to Hilbert». MacTutor History of Mathematics. Archivado desde el original el 29 de septiembre de 2007. Consultado el 30 de agosto de 2006.
- Richman.
- Richman pp. 398–399.
- Griffiths & Hilton §24.2 «Sequences» p. 386.
- Griffiths & Hilton pp. 388, 393.
- Griffiths & Hilton p. 395.
- Griffiths & Hilton pp.viii, 395.
- Petkovšek p. 408.
- Protter and Morrey p. 503; Bartle and Sherbert p. 61.
- Komornik and Loreti p. 636.
- Kempner p. 611; Petkovšek p. 409.
- Petkovšek pp. 410–411.
- Leavitt 1984 p. 301.
- Lewittes pp. 1–3; Leavitt 1967 pp. 669, 673; Shrader-Frechette pp. 96–98.
- Pugh p. 97; Alligood, Sauer, y Yorke pp. 150–152. Protter y Morrey (p. 507) and Pedrick (p. 29) asignan esta descripción como ejercicio.
- Maor (p. 60) y Mankiewicz (p. 151) revisión del método anterior; Mankiewicz se lo atribuye a Cantor, pero la fuente primaria no está clara. Munkres (p. 50) menciona el último método.
- Rudin p. 50, Pugh p. 98.
- Bunch p. 119; Tall y Schwarzenberger p. 6. La última sugerencia es debida a Burrell (p. 28): «Quizá el más asegurado de todos los números es el 1 ... Por lo que es particularmente perturbador cuando se trata de pasar al 0,9~ como 1.»
- Tall y Schwarzenberger pp. 6–7; Tall 2000 p. 221.
- Tall y Schwarzenberger p. 6; Tall 2000 p. 221.
- Tall 2000 p. 221.
- Tall 1976 pp. 10–14.
- Pinto and Tall p. 5, Edwards y Ward pp. 416–417.
- Mazur pp. 137–141.
- Dubinsky et al. 261–262.
- Observado por Richman (p. 396). Hans de Vreught (1994). «sci.math FAQ: Why is 0.9999... = 1?». Consultado el 29 de junio de 2006.
- Cecil Adams (11 de julio de 2003). «An infinite question: Why doesn't .999~ = 1?». The Straight Dope. Chicago Reader. Archivado desde el original el 10 de enero de 2012. Consultado el 6 de septiembre de 2006.
- «Blizzard Entertainment Announces .999~ (Repeating) = 1». Press Release. Blizzard Entertainment. 1 de abril de 2004. Consultado el 16 de noviembre de 2009.
- Renteln and Dundes, p. 27.
- Gowers p. 60.
- Berz 439–442.
- Para un tratamiento exhaustivo del análisis no estándar véase por ejemplo Non-standard Analysis de Robinson.
- Lightstone pp. 245–247.
- Katz & Katz 2010.
- Stewart 2009, p. 175; la discusión completa de 0,999... se extiende hasta pp. 172–175.
- Katz & Katz (2010b).
- R. Ely (2010).
- Véase Hackenbush.
- Berlekamp, Conway, y Guy (pp. 79–80, 307–311) discute 1 y 1/3 y abordan 1/ω. El juego para 0.111...2 sigue directamente de la Regla de Berlekamp.
- Richman pp. 397–399.
- Richman pp. 398–400. Rudin (p. 23) asigna esta esta construcción alternativa (sobre los racionales) como el último ejercicio del capítulo 1.
- Gardiner p. 98; Gowers p. 60.
- Fjelstad p. 11.
- Fjelstad pp. 14–15.
- DeSua p. 901.
- DeSua pp. 902–903.
Bibliografía
- Alligood, Sauer, and Yorke (1996). «4.1 Cantor Sets». Chaos: An introduction to dynamical systems. Springer. ISBN 0-387-94677-2.
- Apostol, Tom M. (1974). Mathematical analysis (2e edición). Addison-Wesley. ISBN 0-201-00288-4.
- Bartle, R.G. and D.R. Sherbert (1982). Introduction to real analysis. Wiley. ISBN 0-471-05944-7.
- Beals, Richard (2004). Analysis. Cambridge UP. ISBN 0-521-60047-2.
- Berlekamp, E.R.; J.H. Conway; and R.K. Guy (1982). Winning Ways for your Mathematical Plays. Academic Press. ISBN 0-12-091101-9.
- Berz, Martin (1992). «Automatic differentiation as nonarchimedean analysis». Computer Arithmetic and Enclosure Methods. Elsevier. pp. 439-450.
- Bunch, Bryan H. (1982). Mathematical fallacies and paradoxes. Van Nostrand Reinhold. ISBN 0-442-24905-5.
- Burrell, Brian (1998). Merriam-Webster's Guide to Everyday Math: A Home and Business Reference. Merriam-Webster. ISBN 0-87779-621-1.
- Byers, William (2007). How Mathematicians Think: Using Ambiguity, Contradiction, and Paradox to Create Mathematics. Princeton UP. ISBN 0-691-12738-7.
- Conway, John B. (1978) [1973]. Functions of one complex variable I (2e edición). Springer-Verlag. ISBN 0-387-90328-3.
- Davies, Charles (1846). The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications. A.S. Barnes.
- DeSua, Frank C. (noviembre de 1960). «A system isomorphic to the reals». The American Mathematical Monthly 67 (9): 900-903. doi:10.2307/2309468.
- Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown (2005). «Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2». Educational Studies in Mathematics 60: 253-266. doi:10.1007/s10649-005-0473-0.
- Edwards, Barbara and Michael Ward (mayo de 2004). «Surprises from mathematics education research: Student (mis)use of mathematical definitions» (PDF). The American Mathematical Monthly 111 (5): 411-425. doi:10.2307/4145268.
- Enderton, Herbert B. (1977). Elements of set theory. Elsevier. ISBN 0-12-238440-7.
- Euler, Leonhard (1822) [1770]. John Hewlett and Francis Horner, English translators., ed. Elements of Algebra (3rd English edición). Orme Longman. ISBN 0387960147.
- Fjelstad, Paul (enero de 1995). «The repeating integer paradox». The College Mathematics Journal 26 (1): 11-15. doi:10.2307/2687285.
- Gardiner, Anthony (2003) [1982]. Understanding Infinity: The Mathematics of Infinite Processes. Dover. ISBN 0-486-42538-X.
- Gowers, Timothy (2002). Mathematics: A Very Short Introduction. Oxford UP. ISBN 0-19-285361-9.
- Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 0-262-07034-0.
- Griffiths, H.B.; Hilton, P.J. (1970). A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation. Londres: Van Nostrand Reinhold. ISBN 0-442-02863-6.
- Katz, K.; Katz, M. (2010a). «When is .999… less than 1?». The Montana Mathematics Enthusiast 7 (1): 3-30. Archivado desde el original el 20 de julio de 2011.
- Kempner, A.J. (diciembre de 1936). «Anormal Systems of Numeration». The American Mathematical Monthly 43 (10): 610-617. doi:10.2307/2300532.
- Komornik, Vilmos; and Paola Loreti (1998). «Unique Developments in Non-Integer Bases». The American Mathematical Monthly 105 (7): 636-639. doi:10.2307/2589246.
- Leavitt, W.G. (1967). «A Theorem on Repeating Decimals». The American Mathematical Monthly 74 (6): 669-673. doi:10.2307/2314251.
- Leavitt, W.G. (septiembre de 1984). «Repeating Decimals». The College Mathematics Journal 15 (4): 299-308. doi:10.2307/2686394.
- Lewittes, Joseph (2006). «Midy's Theorem for Periodic Decimals». New York Number Theory Workshop on Combinatorial and Additive Number Theory. arXiv.
- Lightstone, A.H. (marzo de 1972). «Infinitesimals». The American Mathematical Monthly 79 (3): 242-251. doi:10.2307/2316619.
- Mankiewicz, Richard (2000). The story of mathematics. Cassell. ISBN 0-304-35473-2.
- Maor, Eli (1987). To infinity and beyond: a cultural history of the infinite. Birkhäuser. ISBN 3-7643-3325-1.
- Mazur, Joseph (2005). Euclid in the Rainforest: Discovering Universal Truths in Logic and Math. Pearson: Pi Press. ISBN 0-13-147994-6.
- Munkres, James R. (2000) [1975]. Topology (2e edición). Prentice-Hall. ISBN 0-13-181629-2.
- Núñez, Rafael (2006). «Do Real Numbers Really Move? Language, Thought, and Gesture: The Embodied Cognitive Foundations of Mathematics». Springer. pp. 160-181. ISBN 978-0-387-25717-4. Archivado desde el original el 18 de julio de 2011. Consultado el 6 de mayo de 2010.
- Pedrick, George (1994). A First Course in Analysis. Springer. ISBN 0-387-94108-8.
- Peressini, Anthony; Peressini, Dominic (2007). «Philosophy of Mathematics and Mathematics Education». En Bart van Kerkhove, Jean Paul van Bendegem, ed. Perspectives on Mathematical Practices. Logic, Epistemology, and the Unity of Science 5. Springer. ISBN 978-1-4020-5033-6.
- Petkovšek, Marko (mayo de 1990). «Ambiguous Numbers are Dense». American Mathematical Monthly 97 (5): 408-411. doi:10.2307/2324393.
- Pinto, Márcia and David Tall (2001). «Following students' development in a traditional university analysis course». PME25. pp. v4: 57-64. Consultado el 3 de mayo de 2009.
- Protter, M.H. and C.B. Morrey (1991). A first course in real analysis (2e edición). Springer. ISBN 0-387-97437-7.
- Pugh, Charles Chapman (2001). Real mathematical analysis. Springer-Verlag. ISBN 0-387-95297-7.
- Renteln, Paul and Allan Dundes (enero de 2005). «Foolproof: A Sampling of Mathematical Folk Humor» (PDF). Notices of the AMS 52 (1): 24-34. Consultado el 3 de mayo de 2009.
- Richman, Fred (diciembre de 1999). «Is 0.999… = 1?». Mathematics Magazine 72 (5): 396-400. Free HTML preprint: Richman, Fred (8 de junio de 1999). «Is 0.999… = 1?». Archivado desde el original el 3 de febrero de 2006. Consultado el 23 de agosto de 2006. Note: the journal article contains material and wording not found in the preprint.
- Robinson, Abraham (1996). Non-standard analysis (Revised edición). Princeton University Press. ISBN 0-691-04490-2.
- Rosenlicht, Maxwell (1985). Introduction to Analysis. Dover. ISBN 0-486-65038-3.
- Rudin, Walter (1976) [1953]. Principles of mathematical analysis (3e edición). McGraw-Hill. ISBN 0-07-054235-X.
- Shrader-Frechette, Maurice (marzo de 1978). «Complementary Rational Numbers». Mathematics Magazine 51 (2): 90-98.
- Smith, Charles and Charles Harrington (1895). Arithmetic for Schools. Macmillan.
- Sohrab, Houshang (2003). Basic Real Analysis. Birkhäuser. ISBN 0-8176-4211-0.
- Stewart, Ian (1977). The Foundations of Mathematics. Oxford UP. ISBN 0-19-853165-6.
- Stewart, Ian (2009). Professor Stewart's Hoard of Mathematical Treasures. Profile Books. ISBN 978-1-84668-292-6.
- Stewart, James (1999). Calculus: Early transcendentals (4e edición). Brooks/Cole. ISBN 0-534-36298-2.
- D.O. Tall and R.L.E. Schwarzenberger (1978). «Conflicts in the Learning of Real Numbers and Limits» (PDF). Mathematics Teaching 82: 44-49. Consultado el 3 de mayo de 2009.
- Tall, David (1976/7). «Conflicts and Catastrophes in the Learning of Mathematics» (PDF). Mathematical Education for Teaching 2 (4): 2-18. Consultado el 3 de mayo de 2009.
- Tall, David (2000). «Cognitive Development In Advanced Mathematics Using Technology» (PDF). Mathematics Education Research Journal 12 (3): 210-230. Consultado el 3 de mayo de 2009.
- von Mangoldt, Dr. Hans (1911). «Reihenzahlen». Einführung in die höhere Mathematik (en alemán) (1st edición). Leipzig: Verlag von S. Hirzel.
- Wallace, David Foster (2003). Everything and more: a compact history of infinity. Norton. ISBN 0-393-00338-8.
Enlaces externos
 Wikimedia Commons alberga una galería multimedia sobre 0,999….
Wikimedia Commons alberga una galería multimedia sobre 0,999….