Punto de Spieker

En geometría, el punto de Spieker o centro de Spieker es un punto especial asociado con un triángulo. Se define como el centro de masa del perímetro del triángulo. El centro de Spieker de un triángulo ABC es el centro de gravedad de una estructura de alambre homogénea en forma de triángulo ABC.[1][2] El punto recibe su nombre en honor al geómetra alemán del siglo XIX Theodor Spieker.[3] El punto de Spieker es un centro triangular y aparece como el punto X(10) en la Enciclopedia de Centros del Triángulo de Clark Kimberling.

Ubicación
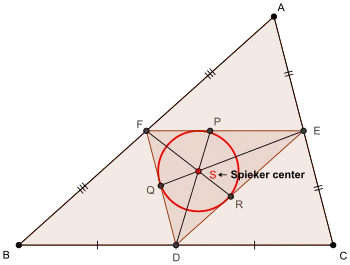
El punto de Spieker del triángulo ABC es el incentro del triángulo medial del triángulo ABC

El siguiente resultado se puede utilizar para localizar el centro de Spieker de cualquier triángulo.[1]

El punto de Spieker del triángulo ABC es el incentro del triángulo medial del triángulo ABC.

Es decir, el centro de Spieker del triángulo ABC es el centro de la circunferencia inscrita en el triángulo medial del triángulo ABC. Este círculo se conoce como la circunferencia de Spieker.

El centro de Spieker también se encuentra en la intersección de las tres cuchillas del triángulo ABC. Una cuchilla de un triángulo es un segmento de línea que biseca el perímetro del triángulo y tiene un punto final en el punto medio de uno de los tres lados. Cada cuchilla contiene el centro de masa del límite del triángulo ABC, por lo que las tres cuchillas se encuentran en el centro de Spieker.

Para ver que el incentro del triángulo medial coincide con el punto de intersección de las cuchillas, considere una estructura de alambre homogénea en forma de triángulo ABC que consta de tres alambres en forma de segmentos de línea que tienen longitudes a, b, c. La estructura de alambre tiene el mismo centro de masa que un sistema de tres partículas de masas a, b, c colocadas en los puntos medios D, E, F de los lados BC, CA, AB. El centro de masa de las partículas en E y F es el punto P que divide el segmento EF en la relación c: b. La línea DP es la bisectriz interna de ∠D. Por tanto, el centro de masa del sistema de tres partículas se encuentra en la bisectriz interna de ∠D. Argumentos similares muestran que el centro de masa del sistema de tres partículas también se encuentra en las bisectrices internas de ∠E y ∠F. De ello se deduce que el centro de masa de la estructura de alambre es el punto de concurrencia de las bisectrices internas de los ángulos del triángulo DEF, que es el incentro del triángulo medial DEF.

Propiedades
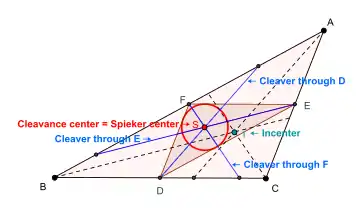
El centro de Spieker, centro de las cuchillas de un triángulo

Sea S el punto de Spieker del triángulo ABC.

bc (b + c) : ca (c + a) : ab (a + b).[4]
b + c : c + a : a + b .[4]
Por lo tanto, en una recta numérica adecuadamente escalada y posicionada, I = 0, G = 2, S = 3 y M = 6.
  • S se encuentra en la hipérbola de Kiepert. S es el punto de coincidencia de las líneas AX, BY y CZ donde XBC, YCA y ZAB son trinágulos similares, isósceles y situados de manera similar construidos en los lados del triángulo ABC como bases, que tienen el ángulo de base común tan−1 [ tan(A/2) tan(B/2) tan(C/2) ].[7]

Referencias
  1. Honsberger, Ross (1995). Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Mathematical Association of America. pp. 3–4.
  2. Kimberling, Clark. «Spieker center». Consultado el 5 de mayo de 2012.
  3. Spieker, Theodor (1888). Lehrbuch der ebenen Geometrie. Potsdam, Germany.
  4. Kimberling, Clark. «Encyclopedia of Triangle Centers». Consultado el 5 de mayo de 2012.
  5. Odenhal, Boris (2010), «Some triangle centers associated with the circles tangent to the excircles», Forum Geometricorum 10: 35-40.
  6. Bogomolny, A.. «Nagel Line from Interactive Mathematics Miscellany and Puzzles». Consultado el 5 de mayo de 2012.
  7. Weisstein, Eric W. «Kiepert Hyperbola». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.