Circuncónica e incónica
En la geometría del triángulo, una circuncónica es una curva cónica que pasa por los tres vértices de un triángulo dado,[1] y una incónica es una curva cónica inscrita en los lados (incluso extendidos) de un triángulo.[2]
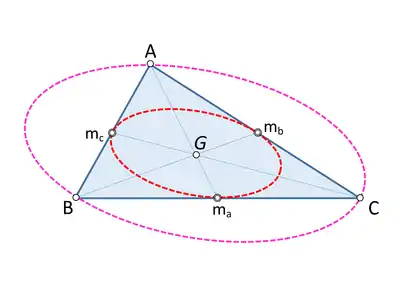
Supóngase que A, B, C son distintos puntos no colineales, y que ΔABC designa el triángulo cuyos vértices son A, B, C. Siguiendo la práctica común, A denota no solo el vértice, sino también el ángulo BAC en el vértice A, y de manera similar para B y C como ángulos en ΔABC. Sean a = |BC|, b = |CA|, c = |AB|, las longitudes de los lados de ΔABC.
En coordenadas trilineales, una circuncónica general es el lugar geométrico de los puntos X = x : y : z que satisfacen la ecuación
- uyz + vzx + wxy = 0,
para algún punto u : v : w. El conjugado isogonal de cada punto X de la circuncónica, que no sea A, B, C, es un punto de la línea
- ux + vy + wz = 0.
Esta línea coincide con la circunferencia circunscrita de ΔABC en 0, 1 o 2 puntos, según la circuncónica sea una elipse, una parábola o una hipérbola.
Una incónica general es tangente a las tres líneas rectas laterales de ΔABC y está dada por la ecuación
- u2x2 + v2y2 + w2z2 − 2vwyz − 2wuzx − 2uvxy = 0.
Centros y líneas tangentes
Circuncónica
El centro de una circuncónica general es el punto
- u (− au + bv + cw) : v (au − bv + cw) : w (au + bv − cw).
Las líneas tangentes a una circuncónica general en los vértices A, B, C son, respectivamente,
- wv + vz = 0,
- uz + wx = 0,
- vx + uy = 0.
Incónica
El centro de una incónica general es el punto
- cy + bz : az + cx : bx + ay.
Las líneas tangentes a una incónica general son las líneas rectas laterales de ΔABC, dadas por las ecuaciones x = 0, y = 0, z = 0.
Otras características
Circuncónica
- Cada circuncónica no circular se corta con la circunferencia circunscrita de ΔABC en un punto que no sea A, B o C, a menudo llamado el cuarto punto de intersección, dado por las coordenadas trilineales
- (cx − az) (ay − bx) : (ay − bx) (bz − cy) : (bz − cy) (cx − az)
- Si P = p : q : r es un punto en una circuncónica general, entonces la tangente a la cónica en P viene dada por
- (vr + wq) x + (wp + ur) y + (uq + vp) z = 0.
- La circuncónica general se reduce a una parábola si y solo si
- u2a2 + v2b2 + w2c2 − 2vwbc − 2wuca − 2vavab = 0,
- y a una hipérbola si y solo si
- u cos A + v cos B + w cos C = 0.
- De todos los triángulos inscritos en una elipse dada, el centroide del que tiene el área más grande coincide con el centro de la elipse.[3]: p.147 La elipse dada, pasando por los tres vértices de este triángulo y centrada en el centroide del triángulo, se llama circunelipse de Steiner.
Incónica
- Una incónica general se reduce a una parábola si y solo si
- ubc + vca + wab = 0,
- en cuyo caso es tangente externamente a uno de los lados del triángulo y es tangente a los otros dos lados extendidos.
- Supóngase que p1 : q1 : r1 y p2 : q2 : r2 son puntos distintos, y sea
- X = (p1 + p2t) : (q1 + q2t) : (r1 + r2t).
- Como el parámetro t se extiende a través del dominio de los números reales, el lugar geométrico de X es una recta. Definiendo
- X2 = (p1 + p2t) 2 : (q1 + q2t) 2 : (r1 + r2t)2,
- el lugar geométrico de X2 es la incónica, necesariamente una elipse, dada por la ecuación
- L4x2 + M4y2 + N4z2 − 2M2N2yz − 2N2L2zx − 2L2M2xy = 0,
- donde
- L = q1r2 − r1q2,
- M = r1p2 − p1r2,
- N = p1q2 − q1p2.
- Un punto en el interior de un triángulo es el centro de una inelipse del propio triángulo si y solo si el punto se encuentra en el interior del triángulo cuyos vértices se encuentran en los puntos medios de los lados del triángulo original.[3]: p.139 Para un punto dado dentro del triángulo medial, la inelipse con su centro en ese punto es única.[3]: p.142
- La inelipse con el área más grande es la inelipse de Steiner, también llamada la inelipse del punto medio, con su centro en el centroide[3]: p.145 del triángulo. En general, la relación entre el área de la inelipse y el área del triángulo, en términos de las coordenadas baricéntricas de suma unidad del centro de la inelipse, es[3]: p.143
- que se maximiza para las coordenadas baricéntricas del centroide
- Las líneas que conectan los puntos de tangencia de cualquier inelipse de un triángulo con los vértices opuestos del triángulo son concurrentes.[3]: p.148
Extensión a los cuadriláteros
Todos los centros de inelipses de un cuadrilátero dado caen en el segmento de línea recta que conecta los puntos medios de las diagonales del cuadrilátero.[3]: p.136
Ejemplos
- Circuncónicas
- Circunferencia circunscrita, la única circunferencia que pasa por los tres vértices de un triángulo
- Circunelipse de Steiner, la única elipse que pasa por los tres vértices de un triángulo y tiene su centro en el centroide del triángulo
- Hipérbola de Kiepert, la única cónica que pasa por los tres vértices de un triángulo, su centroide y su ortocentro
- Hipérbola de Jeřábek, una hipérbola centrada en la circunferencia de los nueve puntos de un triángulo y que pasa por los tres vértices del triángulo, así como su circunferencia circunscrita, ortocentro y varios otros centros notables
- Hipérbola de Feuerbach, una hipérbola equilátera que pasa a través del ortocentro de un triángulo, del punto de Nagel y de varios otros puntos notables, y tiene su centro en el círculo de nueve puntos.
- Incónicas
- Incírculo, el único círculo que es internamente tangente a los tres lados de un triángulo
- Inelipse de Steiner, la única elipse que es tangente a los tres lados de un triángulo en sus puntos medios
- Inelipse de Mandart, la única elipse tangente a los lados de un triángulo en los puntos de contacto de sus excircunferéncias
- Parábola de Kiepert
- Parábola de Yff
Referencias
- Weisstein, Eric W. "Circumconic." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Circumconic.html
- Weisstein, Eric W. "Inconic." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Inconic.htm (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- Chakerian, G. D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979.
Enlaces externos
- Circumconic en MathWorld
- Inconic en MathWorld