Lado extendido

En un triángulo obtuso, las alturas de los vértices contrarios al ángulo de más de 90°, se cruzan con los lados de la base correspondiente extendida, pero no con los lados de la base.

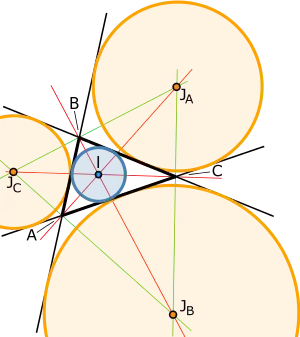
Las circunferencias exinscritas de un triángulo, así como las incónicas del triángulo que no son elipses, son externamente tangentes a un lado del triángulo y a los otros dos lados extendidos.

Las coordenadas trilineales ubican un punto en el plano por sus distancias relativas desde los lados extendidos de un triángulo de referencia. Si el punto está fuera del triángulo, la perpendicular desde el punto hasta la línea lateral puede encontrarse con la línea lateral fuera del triángulo, es decir, no en el lado real del triángulo.

En un triángulo, tres puntos de intersección, cada uno de la bisectriz de un ángulo interior con el lado extendido opuesto, son colineales.[1]^{: p. 149}

En un triángulo, tres puntos de intersección, dos de ellos entre una bisectriz ángulo interior y el lado opuesto, y el tercero entre la otra bisectriz de ángulo exterior y el lado opuesto extendido, son colineales.[1]^{: p. 149}

Un cuadrilatero extratangencial ABCD y sus excircunferencias

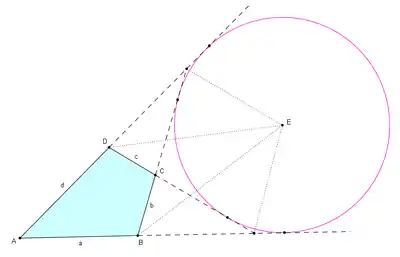
Un cuadrilatero extratangencial permite trazar una circunferencia que es tangente a los cuatro lados extendidos. El excentro (centro del círculo tangente) se encuentra en la intersección de las seis bisectrices: las bisectrices de los ángulos interiores de dos vértices opuestos, las bisectrices de los ángulos suplementarios exteriores de los otros dos vértices y las bisectrices externas de los ángulos formados donde las extensiones de lados opuestos se cruzan.

Las intersecciones de los lados opuestos extendidos del hexágono inscrito ABCDEF se encuentran en la recta de Pascal MNP (color azul). Los lados extendidos del hexágono están en gris y rojo.

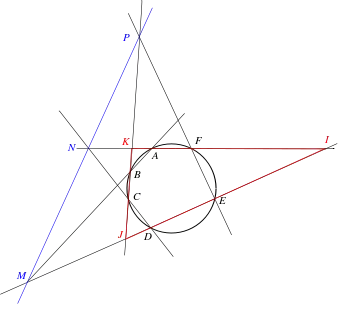
El teorema de Pascal establece que si se eligen seis puntos arbitrarios en una sección cónica (es decir, elipse, parábola o hipérbola) y se unen por segmentos de línea en cualquier orden para formar un hexágono, entonces los tres pares de lados opuestos del hexágono (extendido si es necesario) se encuentran en tres puntos que se sitúan en una línea recta, llamada recta de Pascal del hexágono.