Defecto angular

Para un poliedro, el defecto en un vértice es igual a 2π menos la suma de todos los ángulos en el vértice (incluyendo todas las caras convergentes en el vértice). Si un poliedro es convexo, entonces el defecto de cada vértice es siempre positivo. Si la suma de los ángulos excede un giro completo, como ocurre en algunos vértices de muchos poliedros no convexos, entonces el defecto es negativo.

El concepto de defecto se extiende a dimensiones más altas como la cantidad por la que la suma de los ángulos diedros de las caras concurrentes en un vértice no alcanza un círculo completo.

El defecto de cualquiera de los vértices de un dodecaedro regular (en el que tres pentágonos regulares se encuentran en cada vértice) es 36°, o π/5 radianes, o 1/10 de un círculo. Cada uno de los ángulos mide 108°; y tres de estos ángulos se encuentran en cada vértice, por lo que el defecto es 360° - (108° + 108° + 108°) = 36°.

Se puede seguir el mismo procedimiento para los otros sólidos platónicos:

Forma	Número de vértices	Polígonos concurrentes en cada vértice	Defecto en cada vértice	Defecto total
Tetraedro	4	Tres triángulos equiláteros	${\displaystyle \pi \ \ (180^{\circ })}$	${\displaystyle 4\pi \ \ (720^{\circ })}$
Octaedro	6	Cuatro triángulos equiláteros	${\displaystyle {2\pi \over 3}\ (120^{\circ })}$	${\displaystyle 4\pi \ \ (720^{\circ })}$
Cubo	8	Tres cuadrados	${\displaystyle {\pi \over 2}\ \ (90^{\circ })}$	${\displaystyle 4\pi \ \ (720^{\circ })}$
Icosaedro	12	Cinco triángulos equiláteros	${\displaystyle {\pi \over 3}\ \ (60^{\circ })}$	${\displaystyle 4\pi \ \ (720^{\circ })}$
Dodecaedro	20	Tres pentágonos regulares	${\displaystyle {\pi \over 5}\ \ (36^{\circ })}$	${\displaystyle 4\pi \ \ (720^{\circ })}$

El teorema de Descartes sobre el "defecto total" de un poliedro establece que si el poliedro es homeomorfo a una esfera (es decir, topológicamente equivalente a una esfera, de modo que puede deformarse para acomodarse sobre una esfera estirándose sin romperse), el "defecto total", es decir, la suma de los defectos de todos los vértices, es dos círculos completos (o 720° o 4π radianes). El poliedro no necesita ser convexo.[1]

Una generalización dice que el número de círculos en el defecto total es igual a la característica de Euler del poliedro. Este es un caso especial del teorema de Gauss-Bonnet, que relaciona la integral de la curvatura gaussiana con la característica de Euler. Aquí la curvatura gaussiana se concentra en los vértices: en las caras y bordes, la curvatura gaussiana es cero y la integral de la curvatura gaussiana en un vértice es igual al defecto angular en ese punto.

Esto se puede usar para calcular el número V de vértices de un poliedro sumando los ángulos de todas las caras y sumando el defecto total. Este total tendrá un círculo completo para cada vértice en el poliedro. Se debe tener cuidado al usar la característica de Euler correcta para el poliedro.

El teorema de singularidad de Alexandrov da una respuesta a esta cuestión, demostrando que un espacio métrico que es localmente euclídeo, excepto por un número finito de puntos de defecto angular positivo, que se suma a 4π, se puede concretar de una manera única como la superficie de un poliedro convexo.

Poliedros con defectos positivos

Es tentador pensar que cada poliedro no convexo debe tener algunos vértices cuyo defecto es negativo, pero este no tiene por qué ser el caso. Dos contraejemplos a esta afirmación son el pequeño dodecaedro estrellado y el gran dodecaedro estrellado, que tienen doce vértices convexos, cada uno con defectos positivos.

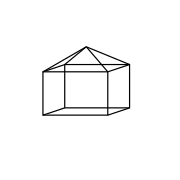
Un contraejemplo de un poliedro que no se interseca consigo mismo es proporcionado por un cubo en el que una cara es reemplazada por una pirámide cuadrada: esta pirámide cuadrada alargada es convexa y los defectos en cada vértice son positivos. Ahora considérese el mismo cubo pero con la pirámide cuadrada entrando en el cubo: esta figura es cóncava, pero los defectos siguen siendo los mismos y todos son positivos.

El defecto negativo indica que el vértice se asemeja a un punto de silla de montar, mientras que el defecto positivo indica que el vértice se asemeja a un máximo o mínimo local.

• Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton (2008), Pages 220–225.

• Weisstein, Eric W. «Angular defect». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.