Poliedro toroidal

En geometría, un poliedro toroidal es un tipo de poliedro que también es un toroide (un toro con g orificios), que tiene un género topológico de 1 o más. Ejemplos notables incluyen los poliedros de Császár y de Szilassi.

Es posible construir un toro poliédrico para aproximar una superficie tórica a partir de una red de caras con forma de cuadrilátero, como en este ejemplo de 6x4

Variaciones en la definición

Los poliedros toroidales se definen como colecciones de polígonos que se encuentran en sus bordes y vértices, formando una variedad con dos propiedades particulares:: cada arista debe ser compartida por exactamente dos caras polígonales, y el enlace de cada vértice debe formar un solo ciclo en el que se alternan entre las aristas y los polígonos que se encuentran en ese vértice. Para los poliedros toroidales, esta variedad además es una superficie orientable.[1] Algunos autores restringen la frase "poliedros toroidales" para que signifique más específicamente poliedros topológicamente equivalentes a un toro (es decir, de género 1).[2]

En esta área, es importante distinguir los poliedros toroidales incrustados (cuyas caras son polígonos planos en el espacio euclidiano tridimensional que no se cruzan entre sí), de los poliedros abstractos (superficies topológicas sin ninguna realización geométrica específica).[3] Intermedios entre estos dos extremos son los poliedros formados por polígonos geométricos o por polígonos de estrella en el espacio euclidiano (que se pueden cruzar entre sí).

En todos estos casos, la naturaleza toroidal de un poliedro se puede verificar por su orientabilidad y por su característica de Euler, que no es positiva. La característica de Euler se generaliza a V − A + L = 2 − 2N, donde N es el número de agujeros.

Poliedros de Császár y Szilassi
Modelo interactivo de un poliedro de Szilassi, con cada cara de un color diferente. En la imagen SVG, muévase el ratón hacia la izquierda y hacia la derecha para rotarlo.[4]
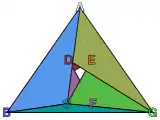Modelo interactivo de un poliedro de Csaszar. En la imagen SVG, muévase el ratón para rotarlo.[5]

Dos de los poliedros toroidales incrustados más simples posibles son los poliedros de Császár y Szilassi.

El poliedro de Császár es una figura toroidal de siete vértices con 21 aristas y 14 caras triangulares.[6] Este y el tetraedro son los únicos poliedros conocidos en los que cada segmento de línea posible que conecta dos vértices forma una arista del poliedro.[7] Su dual, el poliedro de Szilassi, tiene siete caras hexagonales adyacentes entre sí,[8] e implica la mitad del teorema del número mínimo de colores necesarios para colorear un mapa en un toro (género uno), que es siete.[9]

El poliedro de Császár tiene la menor cantidad de vértices posibles de cualquier poliedro toroidal incrustado, y el poliedro de Szilassi tiene la menor cantidad de caras posibles de cualquier poliedro toroidal incrustado.

Toroides de Stewart

Una categoría especial de poliedros toroidales está construida exclusivamente por caras poligonales regulares, sin cruces, y con una restricción adicional de que las caras adyacentes no deben estar en el mismo plano entre sí, denominados toroides de Stewart[10] (en memoria de Bonnie Stewart, que los estudió intensamente).[11] Son análogos a los sólidos de Johnson en el caso de los poliedros convexos. Sin embargo, a diferencia de los sólidos de Johnson, hay infinitos toroides de Stewart.[12] Incluyen también a los deltaedros toroidales, poliedros cuyas caras son todas triángulos equiláteros.

Una clase restringida de toroides de Stewart, también definidos por Stewart, son los poliedros toroidales cuasi convexos. Estos son los toroides de Stewart que incluyen todos los bordes de sus envolventes convexas. Para estos poliedros, cada cara de la envolvente convexa se encuentra en la superficie del toroide o es un polígono cuyos bordes se encuentran en la superficie del toroide.[13]

Toroides de Stewart por aumento de un solo poliedro
Género 1 1
Imagen
Poliedros 6 prismas hexagonales 8 octaedros
Vértices 48 24
Bordes 84 72
Caras 36 48
Toroides de Stewart por aumento mixto
Género 1 3 11 3 5 5 7 7 11
Imagen
Poliedros 4 cúpulas cuadradas
8 tetraedros		 6 cúpulas triangulares
6 pirámides cuadradas		 4 cúpulas triangulares
6 pirámides cuadradas		 24 prismas triangulares
6 pirámides cuadradas
8 tetraedros		 6 cúpulas cuadradas
4 cúpulas triangulares
12 cubos		 8 cúpulas triangulares
12 cubos		 6 cúpulas cuadradas
12 cubos		 6 cúpulas cuadradas
8 cúpulas triangulares
Vértices 32 30 30 62 72 72 72 72
Bordes 64 60 60 72 168 144 168 168 168
Caras 32 30 38 86 68 88 84 76

Poliedros autosecantes

Octahemioctaedro
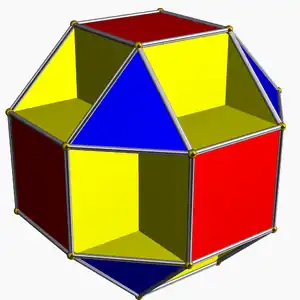Pequeño cubicuboctaedro
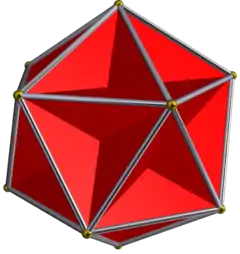Gran dodecaedro

Un poliedro que está formado por un sistema de polígonos cruzados corresponde a una variedad topológica abstracta formada por sus polígonos y su sistema de bordes y vértices compartidos, y el género del poliedro puede determinarse a partir de esta variedad abstracta. Los ejemplos incluyen el octahemioctaedro del género 1, el cubicuboctaedro pequeño del género 3 y el gran dodecaedro del género 4.

Poliedros corona
Estefanoide pentagonal. Presenta simetría diédrica pentagonal y tiene los mismos vértices que el prisma pentagonal uniforme.

Un poliedro corona o estefanoide es una figura toroidal que también es noble, siendo tanto isogonal (vértices iguales) como isoédrico (caras iguales). Los poliedros corona son auto intersecantes y topológicamente auto duales.[14]

Véase también

Referencias
  1. Whiteley (1979);Stewart (1980), p. 15.
  2. Webber, William T. (1997), «Monohedral idemvalent polyhedra that are toroids», Geometriae Dedicata 67 (1): 31-44, doi:10.1023/A:1004997029852.
  3. Whiteley, Walter (1979), «Realizability of polyhedra», Structural Topology (1): 46-58, 73..
  4. Branko Grünbaum, Lajos Szilassi, Geometric Realizations of Special Toroidal Complexes, Contributions to Discrete Mathematics, Volume 4, Number 1, Pages 21-39, ISSN 1715-0868
  5. Ákos Császár, A Polyhedron Without Diagonals. Archivado el 18 de septiembre de 2017 en Wayback Machine., Bolyai Institute, University of Szeged, 1949
  6. Császár, A. (1949), «A polyhedron without diagonals», Acta Sci. Math. Szeged 13: 140-142..
  7. Ziegler, Günter M. (2008), «Polyhedral Surfaces of High Genus», en Bobenko, A. I.; Schröder, P.; Sullivan et al., eds., Discrete Differential Geometry, Oberwolfach Seminars 38, Springer-Verlag, pp. 191-213, ISBN 978-3-7643-8620-7, doi:10.1007/978-3-7643-8621-4_10 ..
  8. Szilassi, Lajos (1986), «Regular toroids», Structural Topology 13: 69-80.Uso incorrecto de la plantilla enlace roto (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última)..
  9. Heawood, P. J. (1890), «Map colouring theorems», Quarterly J. Math. Oxford Ser. 24: 322-339.
  10. Webb, Robert (2000), «Stella: polyhedron navigator», Symmetry: Culture and Science 11 (1-4): 231-268..
  11. Stewart, B. M. (1980), Adventures Among the Toroids: A Study of Orientable Polyhedra with Regular Faces (2nd edición), B. M. Stewart, ISBN 978-0-686-11936-4..
  12. Stewart (1980), p. 15.
  13. Stewart (1980), "Quasi-convexity and weak quasi-convexity", pp. 76–79.
  14. Grünbaum, Branko (1994), «Polyhedra with Hollow Faces», Polytopes: Abstract, Convex and Computational, NATO ASI Series C: Mathematical and Physical Series 440, Kluwer Academic Publishers, pp. 43-70, doi:10.1007/978-94-011-0924-6_3.. See in particular p. 60.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.