Distribución PERT
En probabilidad y estadística, la distribución PERT es una familia de distribuciones continuas de probabilidad definida por los valores:
- mínimo (),
- moda, que se suele encontrar como usual o más frecuente () y
- máximo (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): c )
| PERT | ||
|---|---|---|
|
PERT pdf examples.jpg Función de densidad de probabilidad | ||
|
PERT cdf examples.jpg Función de distribución de probabilidad | ||
| Parámetros |
(real) (real) | |
| Dominio | Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle x \in [a,c]\,} | |
| Función de densidad (pdf) |
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \dfrac{(x-a)^{\alpha-1}(c-x)^{\beta-1}} {\Beta(\alpha,\beta)(c-a)^{\alpha+\beta-1}} } where Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \beta = \dfrac{5c-a-4b} {c-a} = 1 + 4 \dfrac{c-b}{c-a}} | |
| Función de distribución (cdf) |
(the regularized incomplete beta function) with Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle z = (x-a)/(c-a)} | |
| Media | ||
| Mediana |
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle I_{\dfrac{1}{2}}^{[-1]}(\alpha,\beta)(c-a) + a } Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \approx a + (c-a) \dfrac{\alpha-1/3}{\alpha+\beta - 2/3} = \dfrac{a + 6 b + c}{8}} | |
| Moda | ||
| Varianza | ||
| Coeficiente de simetría | ||
| Curtosis | Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \dfrac{6[(\alpha - \beta)^2 (\alpha +\beta + 1) - \alpha \beta (\alpha + \beta + 2)]}{\alpha \beta (\alpha + \beta + 2) (\alpha + \beta + 3)}} | |
que una variable puede tomar. Esta distribución es una transformación de la Distribución Beta, la cual tiene cuatro parámetros; con dos supuestos adicionales que son que el valor esperado () es:
y que la varianza (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \sigma^2 ) es:
Por tanto, la media de la distribución se define como la media ponderada de los valores mínimo, más frecuente y máximo que puede tomar la variable, con cuatro veces la ponderación aplicada al valor modal.
Estos supuestos sobre la media y la varianza de la distribución fueron propuestos por primera vez en Clark, 1962[1] para estimar el efecto de la incertidumbre de la duración de las tareas sobre el resultado del cronograma de un proyecto que se evalúa utilizando la Técnica de revisión y evaluación de programas PERT por sus siglas en inglés Program Evaluation Review Technique, de ahí su nombre. Las matemáticas de la distribución resultaron del deseo de los autores de hacer que la desviación estándar sea igual a aproximadamente 1/6 del rango.[2][3]
La distribución PERT se utiliza ampliamente en el análisis de riesgos [4] para representar la incertidumbre del valor de alguna cantidad cuando uno se basa en estimaciones subjetivas, porque los tres parámetros que definen la distribución son intuitivos para el estimador. La distribución PERT se incluye en la mayoría de las herramientas de software de simulación.
Comparación con la distribución triangular
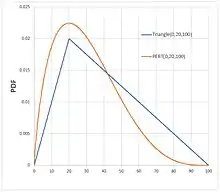
La distribución PERT ofrece una alternativa[5] para usar la Distribución triangular que toma los mismos tres parámetros. La distribución PERT tiene una forma más suave que la distribución triangular, y su desviación estándar es menor; por lo que se suele preferir cuando se tiene mayor confianza en los estimadores. La distribución triangular tiene una media igual a la media de los tres parámetros:
La fórmula pone el mismo énfasis en los valores extremos que generalmente son menos conocidos que el valor más probable y, por lo tanto, pueden verse indebidamente influenciados por una estimación deficiente de un extremo. La distribución triangular también tiene una forma angular que no coincide con la forma más suave que tipifica el conocimiento subjetivo.
La distribución PERT clásica
Como ya se mencionó, en la distribución PERT propuesta por Clark se parte del supuesto de que la varianza de la distribución es:
Y, para calcular la media se tiene:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \mu=\dfrac{a+4\cdot b + c}{6}}
Según Davis,[6] para una distribución Beta en el intervalo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle [a, c]} con parámetros se tiene:
y
Resolviendo para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \alpha y en términos de y se puede notar de manera sencilla que el valor de la fórmula de la media implica que:
y
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \dfrac{\beta}{\alpha+\beta}=\dfrac{c-\mu}{c-a}}
Al poner esto dentro de la formula de la varianza se puede calcular:
Al separar las ecuaciones para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \alpha y , remplazando por y simplificando se obtienen las ecuaciones para los dos parámetros en esta Distribución PERT clásica, así:
y
La distribución PERT modificada
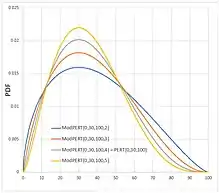
La distribución PERT asigna una probabilidad muy pequeña a los valores extremos, particularmente al extremo más alejado del valor más probable si la distribución está fuertemente sesgada.[7][8] La distribución PERT modificada [9] se propuso para proporcionar más control sobre cuánta probabilidad se asigna a los valores de cola de la distribución.
Según Vose y Hauwermeiren,[10] la PERT modificada«Modified PERT distribution». Vose Software. 2 de mayo de 2017. Consultado el 12 de mayo de 2023. introduce un cuarto parámetro que controla el peso del valor más probable en la determinación de la media:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \mu=\dfrac{a+\gamma\cdot{b}+c}{\gamma+2}}
y con una varianza igual a:
Esta ecuación surge del artículo publicado en 2011 por Herrerías-Velasco y Herrerías-Pleguezuelo,[11] en el que se propone multiplicar la varianza por un valor de ajuste de la siguiente manera:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \sigma^2=\left(\dfrac{c-a}{\gamma+2}\right)^2\cdot\left(\dfrac{5}{7}+\dfrac{16}{7}\cdot\delta\cdot\left(1-\delta\right)\right)} donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \delta=\dfrac{b-a}{c-a}} .
Normalmente, se utilizan valores entre 2 y 4 para , y tienen el efecto de aplanar la curva de densidad. Esto es útil para distribuciones muy sesgadas donde las distancias Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle (b-a),} y son de diferentes tamaños.
Según Vose,[12] cuando , la Distribución PERT es una Distribución Beta en la cual los valores y están dados por:
- y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \beta=\dfrac{\alpha\cdot\left(c-\mu\right)}{\left(\mu-a\right)}} .
Si se remplaza en las anteriores ecuaciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \mu por y se simplifica, se obtienen las ecuaciones más sencillas:
y
Esta forma de calcular los parámetros y son los utilizados en la mayoría de sistemas informáticos de simulación, tales como Crystall Ball de Oracle o @Risk de Palisade.[13]
Implementación en paquetes informáticos
La distribución PERT modificada es implementada en varios paquetes de simulación y lenguajes de programación:
- ModelRisk[14] – risk analysis add-in for Excel.
- Primavera risk analysis – project risk analysis simulation tool.
- Tamara [15] – project risk analysis simulation tool.
- Wolfram (lenguaje de programación)[16] – mathematical symbolic computation program.
- R (lenguaje de programación): mc2d package.[17]
- Python (lenguaje de programación): pertdist package.[18]
Referencias
- Clark CE (1962) The PERT model for the distribution of an activity. Operations Research 10, pp. 405406
- «PERT distribution». Vose Software. 2 de mayo de 2017. Consultado el 16 de julio de 2017.
- Continuous Univariate Distributions - 2nd Ed (1995). Johnson K, Kotz S and Balakkrishnan N. (Section 25.4)
- Cuerpo de conocimientos sobre gestión de proyectos: 6ª Ed. (2017). Project Management Institute Capítulo 6
- Simulation Modeling and Analysis (2000). Law AM and Kelton WD. Section 6.11
- «Teaching note - Teaching project simulation in Excel using PERT - Beta Distributions». INFORMS Transactions on education. 2008. Consultado el 16 de junio de 2021.
- Business Risk and Simulation Modelling in Practice (2015). M Rees. Section 9.1.8
- Risk Analysis – a Quantitative Guide: 3rd Ed. (2008) Vose D
- Paulo Buchsbaum (9 de junio de 2012). «Modified Pert Simulation». Greatsolutions.com.br. Archivado desde el original el 23 de diciembre de 2018. Consultado el 14 de julio de 2017.
- «A Compendium of Distributions (second edition). [ebook]». Vose Software, Ghent, Belgium. 2012. Consultado el 21 de junio de 2021.
- Herrerías-Velasco, José Manuel; Herrerías-Pleguezuelo, Rafael; van Dorp, Johan René (2011). «Revisiting the PERT mean and variance». European Journal of Operational Research 210 (2): 448-451. ISSN 0377-2217. doi:10.1016/j.ejor.2010.08.014.
- «Risk analysis : a quantitative guide». John Wiley and Sons. 2008. Consultado el 9 de junio de 2021.
- «PERT Distribution». Charles Zaiontz. 2017. Consultado el 9 de junio de 2021.
- «Modified PERT distribution». Vose Software. 2 de mayo de 2017. Consultado el 16 de julio de 2017.
- «Probability distributions used in Tamara». Vose Software. 2 de mayo de 2017. Consultado el 16 de julio de 2017.
- «PERTDistribution—Wolfram Language Documentation». Reference.wolfram.com. Consultado el 16 de julio de 2017.
- «Package ‘mc2d’». 6 de marzo de 2017. Consultado el 16 de diciembre de 2020.
- «PertDist». 6 de diciembre de 2020. Consultado el 5 de enero de 2021.