Función de densidad de probabilidad
En la teoría de la probabilidad, la función de densidad de probabilidad, función de densidad, o simplemente densidad de una variable aleatoria continua describe la probabilidad relativa según la cual dicha variable aleatoria tomará determinado valor.
La probabilidad de que la variable aleatoria caiga en una región específica del espacio de posibilidades estará dada por la integral de la densidad de esta variable entre uno y otro límite de dicha región.
La función de densidad de probabilidad (FDP) es positiva a lo largo de todo su dominio y su integral sobre todo el espacio es de valor unitario.
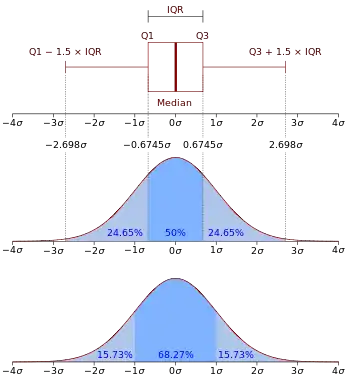
En un sentido más preciso, la FDP se utiliza para especificar la probabilidad de que la variable aleatoria caiga dentro de un rango de valores determinado, en lugar de tomar un valor cualquiera. Esta probabilidad viene dada por la integral de la FDP de esta variable sobre ese rango, es decir, viene dada por el área bajo la función de densidad pero por encima del eje horizontal y entre los valores más bajos y más altos del rango. La función de densidad de probabilidad es no negativa en todas partes, y el área bajo la curva completa es igual a 1.
Los términos función de distribución de probabilidad [1] y función de probabilidad[2] también se han utilizado a veces para denotar la función de densidad de probabilidad. Sin embargo, este uso no es estándar entre probabilistas y estadísticos. En otras fuentes, "función de distribución de probabilidad" puede utilizarse cuando la distribución de probabilidad se define como una función sobre conjuntos generales de valores o puede referirse a la función de distribución acumulativa, o puede ser una función de masa de probabilidad (PMF) en lugar de la densidad. "Función de densidad" en sí también se utiliza para la función de masa de probabilidad, lo que lleva a una mayor confusión.[3] En general, sin embargo, la PMF se utiliza en el contexto de variables aleatorias discretas (variables aleatorias que toman valores en un conjunto contable), mientras que la PDF se utiliza en el contexto de variables aleatorias continuas.
Definición
Una función de densidad de probabilidad caracteriza el comportamiento probable de una población en tanto especifica la posibilidad relativa de que una variable aleatoria continua tome un valor cercano a .
Una variable aleatoria tiene función de densidad , siendo una función no-negativa integrable de Lebesgue, si:
si es la función de distribución de , entonces
y (si es continua en )
Intuitivamente, puede considerarse como la probabilidad de de caer en el intervalo infinitesimal .
Definición formal
La definición formal de la función de densidad requiere de conceptos de la teoría de la medida.
Una variable aleatoria continua con valores en un espacio medible (habitualmente con los conjuntos Borel como subconjuntos medibles), tiene como distribución de probabilidad la medida X∗P en : la densidad de con respecto a la medida de referencia sobre es la derivada de Radon–Nikodym.
esto es, es una función medible con la siguiente propiedad:
para todo conjunto medible .
Discusión
En el caso univariante continuo anterior, la medida de referencia es la medida de Lebesgue. La función de masa de probabilidad de una variable aleatoria discreta es la densidad con respecto a la medida de recuento sobre el espacio muestral (normalmente el conjunto de enteros, o algún subconjunto del mismo).
No es posible definir una densidad con referencia a una medida arbitraria (por ejemplo, no se puede elegir la medida de recuento como referencia para una variable aleatoria continua). Además, cuando existe, la densidad es casi única, lo que significa que dos densidades cualesquiera coinciden casi en todas partes.
Propiedades
De las propiedades de la función de densidad se siguen las siguientes propiedades de la fdp (a veces visto como pdf del inglés):
- para toda .
- El área total encerrada bajo la curva es igual a 1:
- La probabilidad de que tome un valor en el intervalo es el área bajo la curva de la función de densidad en ese intervalo o lo que es lo mismo, la integral definida en dicho intervalo. La gráfica f(x) se conoce a veces como curva de densidad.
Algunas FDP están declaradas en rangos de a , como la de la distribución normal.
Más detalles
A diferencia de una probabilidad, una función de densidad de probabilidad puede tomar valores mayores que uno; por ejemplo, la distribución uniforme en el intervalo [0, 1/2] tiene densidad de probabilidad f(x) = 2 para 0 ≤ x ≤ 1/2 y f(x) = 0 en el resto. La distribución normal estándar tiene densidad de probabilidad
Si una variable aleatoria X está dada y su distribución admite una función de densidad de probabilidad f, entonces el valor esperado de X (si el valor esperado existe) puede calcularse como
No todas las distribuciones de probabilidad tienen función de densidad: las distribuciones de variables aleatorias discretas no la tienen; tampoco la distribución de Cantor, aunque no tiene componente discreta, es decir, no asigna probabilidad positiva a ningún punto individual.
Una distribución tiene una función de densidad si y sólo si su función de distribución acumulativa F(x) es absolutamente continua. En este caso: F es en casi todas partes diferenciable, y su derivada puede usarse como densidad de probabilidad:
Si una distribución de probabilidad admite una densidad, entonces la probabilidad de todo conjunto unipunto {a} es cero; lo mismo vale para conjuntos finitos y contables.
Dos densidades de probabilidad f y g representan la misma distribución de probabilidad precisamente si difieren sólo en un conjunto de Lebesgue medida cero.
En el campo de la física estadística, una reformulación no formal de la relación anterior entre la derivada de la función de distribución acumulativa y la función de densidad de probabilidad se utiliza generalmente como definición de la función de densidad de probabilidad. Esta definición alternativa es la siguiente:
Si dt es un número infinitamente pequeño, la probabilidad de que X esté incluido dentro del intervalo (t, t + dt) es igual a f(t) dt, o:
Distribuciones univariantes absolutamente continuas
Una función de densidad de probabilidad se asocia más comúnmente con distribuciones univariantes absolutamente continuas. Una variable aleatoria tiene densidad , donde es una función integrable de Lebesgue no negativa, si:
Por tanto, si es la función de distribución acumulativa de , entonces:
y (si es continua en )
Intuitivamente, se puede pensar en como la probabilidad de que caiga dentro del intervalo infinitesimal . .
Densidades asociadas con múltiples variables
Para variables aleatorias continuas es posible definir una función de probabilidad de densidad, esta es llamada función de densidad conjunta. La función de densidad conjunta está definida como una función de variables, tal que para cualquier dominio en el espacio -dimensional de los valores de las variables , la probabilidad de ocurrencia de un conjunto de variables se encuentre dentro de es
Si es la función de distribución del vector entonces la función de densidad conjunta puede obtenerse como una derivada parcial
Densidad marginal
Para sea la función de densidad asociada con la variable , esta función es llamada función de densidad marginal y puede ser obtenida a partir de la función de densidad conjunta asociada con las variables como
Relación entre distribuciones discretas y continuas
Es posible representar ciertas variables aleatorias discretas, así como variables aleatorias que implican tanto una parte continua como una discreta, con una función generalizada función de densidad de probabilidad utilizando la Función delta de Dirac. (Esto no es posible con una función de densidad de probabilidad en el sentido definido anteriormente, puede hacerse con una distribución.) Por ejemplo, consideremos una variable aleatoria discreta binaria que tiene la distribución de Rademacher-es decir, que toma -1 o 1 por valores, con probabilidad ![]() cada uno. La densidad de probabilidad asociada a esta variable es:
cada uno. La densidad de probabilidad asociada a esta variable es:
De forma más general, si una variable discreta puede tomar n valores distintos entre números reales, entonces la función de densidad de probabilidad asociada es:
donde son los valores discretos accesibles a la variable y son las probabilidades asociadas a estos valores.
Esto unifica sustancialmente el tratamiento de las distribuciones de probabilidad discretas y continuas. La expresión anterior permite determinar características estadísticas de dicha variable discreta (como la media, la varianza y la curtosis), partiendo de las fórmulas dadas para una distribución continua de la probabilidad.
Suma de variables aleatorias independientes
La función de densidad de la suma de dos variables aleatorias independientes y , cada una de ellas con función de densidad, es la convolución de sus funciones de densidades:
Es posible generalizar el resultado anterior a la suma de variables aleatorias independientes con densidades
Familias de densidades
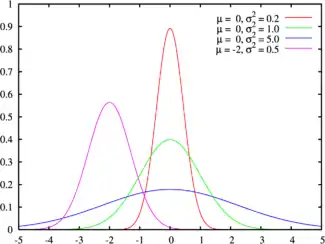
Es habitual que las funciones de densidad de probabilidad (y las funciones de masa de probabilidad) estén parametrizadas, es decir, que se caractericen por parámetros no especificados. Por ejemplo, la distribución normal se parametriza en términos de la media y la varianza, denotadas por y respectivamente, dando la familia de densidades
Diferentes valores de los parámetros describen diferentes distribuciones de diferentes variables aleatorias en el mismo espacio muestral (el mismo conjunto de todos los valores posibles de la variable); este espacio muestral es el dominio de la familia de variables aleatorias que esta familia de distribuciones describe. Un conjunto dado de parámetros describe una única distribución dentro de la familia que comparte la forma funcional de la densidad. Desde la perspectiva de una distribución dada, los parámetros son constantes, y los términos en una función de densidad que contienen sólo parámetros, pero no variables, son parte del factor de normalización de una distribución (el factor multiplicativo que asegura que el área bajo la densidad -la probabilidad de que ocurra algo en el dominio- es igual a 1). Este factor de normalización está fuera del núcleo de la distribución.
Puesto que los parámetros son constantes, re-parametrizar una densidad en términos de parámetros diferentes para dar una caracterización de una variable aleatoria diferente en la familia, significa simplemente sustituir los nuevos valores de los parámetros en la fórmula en lugar de los antiguos.
Ejemplo
Supongamos que las bacterias de una determinada especie viven normalmente de 4 a 6 horas. La probabilidad de que una bacteria viva exactamente 5 horas es igual a cero. Muchas bacterias viven aproximadamente 5 horas, pero no hay ninguna probabilidad de que una determinada bacteria muera exactamente a las 5,00... horas. Sin embargo, la probabilidad de que la bacteria muera entre 5 horas y 5,01 horas es cuantificable. Supongamos que la respuesta es 0,02 (es decir, el 2 %). Entonces, la probabilidad de que la bacteria muera entre las 5 horas y las 5,001 horas debe ser de aproximadamente 0,002, ya que este intervalo de tiempo es una décima parte del anterior. La probabilidad de que la bacteria muera entre 5 horas y 5,0001 horas debería ser de aproximadamente 0,0002, y así sucesivamente.
En este ejemplo, la relación (probabilidad de morir durante un intervalo) / (duración del intervalo) es aproximadamente constante, e igual a 2 por hora (o 2 hora-1). Por ejemplo, hay una probabilidad de 0,02 de morir en el intervalo de 0,01 horas entre 5 y 5,01 horas, y (probabilidad de 0,02 / 0,01 horas) = 2 hora-1. Esta cantidad 2 hora-1 se denomina densidad de probabilidad de morir en torno a las 5 horas. Por tanto, la probabilidad de que la bacteria muera a las 5 horas puede escribirse como (2 hora-1) dt. Esta es la probabilidad de que la bacteria muera dentro de una ventana de tiempo infinitesimal en torno a las 5 horas, donde dt es la duración de esta ventana. Por ejemplo, la probabilidad de que viva más de 5 horas, pero menos de (5 horas + 1 nanosegundo), es (2 horas-1) × (1 nanosegundo) ≈ 6 × 10 - 13 (utilizando la conversión de unidades 3,6 × 1012 nanosegundos = 1 hora).
Existe una función de densidad de probabilidad f con f(5 horas) = 2 horas-1. La integral de f sobre cualquier ventana de tiempo (no sólo ventanas infinitesimales sino también ventanas grandes) es la probabilidad de que la bacteria muera en esa ventana.
Referencias
- Probability distribution functionPlanetMath Archivado el 7 de agosto de 2011 en Wayback Machine.
- Probability Function Archivado el 15 de agosto de 2011 en Wayback Machine. en MathWorld
- Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (por ejemplo, Tabla 5.1 y Ejemplo 5.4)
Enlaces externos
- Simulación de la obtención de la probabilidad en un intervalo a partir de la función de densidad de una variable continua con R (lenguaje de programación)
- Ushakov, N.G. (2001), «Density of a probability distribution», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
Véase también
Bibliografía adicional
- Billingsley, Patrick (1979). Probability and Measure (en inglés). New York, Toronto, London: John Wiley and Sons. ISBN 0-471-00710-2.
- Casella, George; Berger, Roger L. (2002). Statistical Inference (en inglés) (Second edición). Thomson Learning. pp. 34-37. ISBN 0-534-24312-6.
- Stirzaker, David (2003). Elementary Probability (en inglés). ISBN 0-521-42028-8. (requiere registro). Los capítulos 7 al 9 son sobre varaibles continuas.