Distribución de Rayleigh
En la teoría de la probabilidad y estadística, la distribución de Rayleigh es una función de distribución continua. Se suele presentar cuando un vector bidimensional (por ejemplo, el que representa la velocidad del viento) tiene sus dos componentes, ortogonales, independientes y siguen una distribución normal. Su valor absoluto seguirá entonces una distribución de Rayleigh. Esta distribución también se puede presentar en el caso de números complejos con componentes real e imaginaria independientes y siguiendo una distribución normal. Su valor absoluto sigue una distribución de Rayleigh.
| Distribución Rayleigh | ||
|---|---|---|
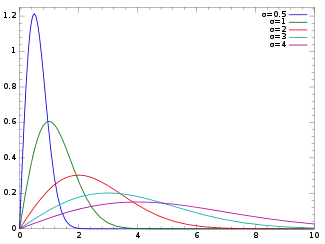 Función de densidad de probabilidad | ||
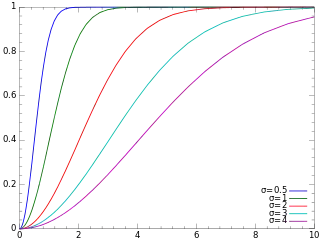 Función de distribución de probabilidad | ||
| Parámetros | ||
| Dominio | ||
| Función de densidad (pdf) | ||
| Función de distribución (cdf) | ||
| Media | ||
| Mediana | ||
| Moda | ||
| Varianza | ||
| Coeficiente de simetría | ||
| Curtosis | ||
| Entropía | ||
| Función generadora de momentos (mgf) | ||
| Función característica | ||
Propiedades
El -ésimo momento de una variable aleatoria es
Estimación por máxima verosimilitud
Dada una muestra de variables aleatorias independientes e idénticamente distribuidas con distribución de Rayleigh con parámetro
es el estimador por máxima verosimilitud de .
Distribuciones relacionadas
- Una variable aleatoria si donde y son variables aleatorias independientes tales que y .
- Si una variable aleatoria entonces sigue una distribución chi-cuadrado con dos grados de libertad, es decir, .
- Si es una variable aleatoria tal que entonces .
- La distribución chi es una generalización de la distribución de Rayleigh.
- La distribución de Rice es una generalización de la distribución de Rayleigh.
- La distribución de Weibull es una generalización de la distribución de Rayleigh.