Distribución χ
En teoría de la probabilidad y estadística, la distribución χ es un tipo de distribución de probabilidad continua. Es la distribución de la raíz cuadrada positiva de la suma de los cuadrados de un conjunto de variables aleatorias independientes, cada una siguiendo un distribución normal estándar o, de manera equivalente, la distribución de la distancia euclidiana de las variables aleatorias desde el origen. Por lo tanto, se relaciona con la distribución χ² al describir la distribución de las raíces cuadradas positivas de una variable que obedece a una distribución chi-cuadrado.
| Distribución χ (Chi) | ||
|---|---|---|
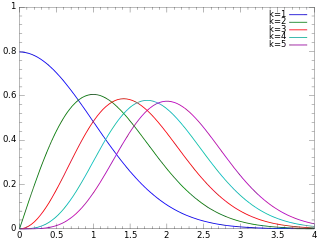 Función de densidad de probabilidad | ||
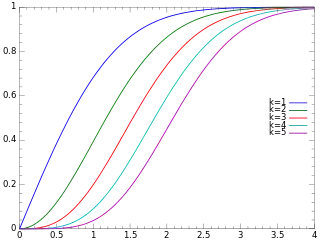 Función de distribución de probabilidad | ||
| Parámetros | (degrees of freedom) | |
| Dominio | ||
| Función de densidad (pdf) | ||
| Función de distribución (cdf) | ||
| Media | ||
| Mediana | ||
| Moda | for | |
| Varianza | ||
| Coeficiente de simetría | ||
| Curtosis | ||
| Entropía |
| |
| Función generadora de momentos (mgf) | Complicada (véase el texto) | |
| Función característica | Complicada (véase el texto) | |
Los ejemplos más familiares son la distribución de Rayleigh (distribución de chi con dos grados de libertad) y la distribución de Boltzmann de las velocidades moleculares en un gas ideal (distribución chi con tres grados de libertad).
Si son k variables aleatorias independientes, normalmente distribuidas con medias y desviaciones típicas , entonces la probabilidad asociada
se distribuye de acuerdo a la distribución chi. En consecuencia, al dividir por la media de la distribución chi (escalada por la raíz cuadrada de n − 1) se obtiene el factor de corrección del sesgo de la desviación típica de la distribución normal. La distribución chi tiene un parámetro: que especifica su número de grados de libertad (es decir, el número de ).
Caracterización
Función de densidad de probabilidad
La función de densidad de probabilidad de la distribución chi es
donde es la función gamma.
Función de distribución acumulativa
La función de distribución acumulada está dada por:
donde es la función gamma incompleta.
Generación de funciones
La función generadora de momentos viene dada por:
donde es una función hipergeométrica confluente de Kummer. Su función característica está dada por:
Propiedades
Momentos
El momento sin procesar viene dado por:
donde es la función gamma. Los primeros momentos simples son:
donde las expresiones de la derecha de cada ecuación se deducen usando la relación de recurrencia para la función gamma:
De estas expresiones se pueden deducir las siguientes relaciones:
Media:
Varianza:
Sesgo:
Exceso de kurtosis:
Distribuciones relacionadas
- Si entonces (Distribución χ²)
- (Distribución normal)
- Si entonces
- Si entonces (Distribución seminormal) para cualquier
- (Distribución de Rayleigh)
- (Distribución de Boltzmann)
- (La norma bidimensional de las variables distribuidas normalmente es una distribución chi con grados de libertad)
- La distribución χ es un caso especial de distribución gamma generalizada o distribución de Nakagami o distribución χ descentrada
| Nombre | Estadística |
|---|---|
| Distribución χ² | |
| Distribución χ² descentrada | |
| Distribución χ | |
| Distribución χ descentrada |