Distribución degenerada
En matemáticas, una distribución degenerada es una distribución de probabilidad en un espacio (discreto o continuo) donde el soporte está necesariamente en un espacio de dimensión más baja. En el caso de una sola variable aleatoria, es una distribución determinista y toma sólo un valor. La distribución satisface la definición de "variable aleatoria" aunque no parezca aleatoria en el sentido común de la palabra, y por ello es considerada como trivial o degenerada. Ejemplos de casos donde se aplica incluyen un dado cayendo en un número cuando todas sus caras son ese mismo número, o un ordenador mostrando un resultado particular cuando está programado para que siempre muestre ese resultado.
| Degenerada de una variable | ||
|---|---|---|
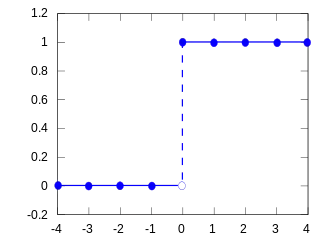 Función de distribución acumulada para k0=0. El eje horizontal es x. Función de distribución de probabilidad | ||
| Parámetros | ||
| Dominio | ||
| Función de densidad (pdf) | ||
| Función de distribución (cdf) | ||
| Media | ||
| Mediana | ||
| Moda | ||
| Varianza | ||
| Coeficiente de simetría | No definido | |
| Curtosis | No definido | |
| Entropía | ||
| Función generadora de momentos (mgf) | ||
| Función característica | ||
En el caso de una sola variable aleatoria real, la distribución degenerada se concentra en un punto en la recta real. La función de masa de la probabilidad es igual a 1 en , y es igual a 0 en cualquier otro lugar.
La distribución degenerada de una variable puede ser vista como el caso limitante de una distribución continua cuya varianza tiende a 0, causando que la función de densidad de la probabilidad sea una delta de Dirac en , con altura infinita allí pero con área bajo la curva igual a 1.
La función de distribución acumulada de la distribución degenerada de una variable es:
Variable aleatoria constante
En teoría de probabilidad, una variable aleatoria constante es una variable aleatoria discreta que toma un valor constante, sin importar qué suceso ocurra. Esto es técnicamente diferente de una variable aleatoria casi seguramente constante, que puede tomar otros valores, pero sólo en sucesos con probabilidad cero. Variables aleatorias constantes y c.s. constantes, las cuales tienen una distribución degenerada, proporcionan una manera de tratar valores constantes
Sea X: Ω → R una variable aleatoria definida en un espacio de probabilidad (Ω, P). Entonces X es una variable aleatoria casi seguramente constante si existe tal que
y es además una variable aleatoria constante si
pero no siempre al revés, ya que si X es casi seguramente constante entonces puede existir γ ∈ Ω tal que X(γ) ≠ k0 (pero entonces necesariamente Pr({γ}) = k0, y de hecho Pr(X ≠ k0) = 0).
Para efectos prácticos, la distinción entre X siendo constante o casi seguramente constante es de poca importancia, ya que la función de distribución acumulada F(x) de X no depende de si X es constante o casi seguramente constante. En los dos casos,
La función F(x) es una función escalonada; en particular es una traslación de la función escalón de Heaviside.