Dodecadodecaedro icositruncado
En geometría, el dodecadodecaedro icositruncado o icosidodecaedro icosidodecatruncado es un poliedro uniforme no convexo, indexado como U45.
| Dodecadodecaedro icositruncado | ||
|---|---|---|
 Imagen del sólido | ||
| Tipo | Poliedro uniforme | |
| Caras | 44 | |
| Polígonos que forman las caras | (20 hexágonos, 12 decágonos, 12 decagramas) | |
| Aristas | 180 | |
| Vértices | 120 | |
| Grupo de simetría | Ih, [5,3], *532 | |
| Poliedro dual | Tridiaquis icosaedro | |
| Símbolo de Wythoff | 3 5 5⁄3 | |
| Símbolo de Coxeter-Dynkin | 57 | |

Modelo 3D de un dodecadodecaedro icositruncado
Envolvente convexa
Su envolvente convexa es un icosidodecaedro truncado no uniforme.
 Icosidodecaedro truncado |
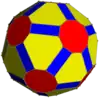 Envolvente convexa |
 Dodecadodecaedro icositruncado |
Coordenadas cartesianas
Las coordenadas cartesianas para los vértices de un dodecadodecaedro icositrunado son todas las permutaciones pares de
- (±(2−1/τ), ±1, ±(2+τ))
- (±1, ±1/τ2, ±(3τ−1))
- (±2, ±2/τ, ±2τ)
- (±3, ±1/τ2, ±τ2)
- (±τ2, ±1, ±(3τ−2))
donde τ = (1+√5)/2 es la proporción áurea (a veces escrita φ).
Poliedros relacionados
Tridiaquis icosaedro
El tridiaquis icosaedro es el poliedro dual del dodecadodecaedro icositruncado. Tiene 44 vértices, 180 aristas y 120 caras triangulares escalenas.
Véase también
- Sólidos de Catalan, duales a los poliedros convexos uniformes
- Poliedros uniformes
- Anexo:Poliedros uniformes
Referencias
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5. Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5. Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5.
Enlaces externos
- Weisstein, Eric W. «Icositruncated dodecadodecahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.