Elipsógrafo

Elipsógrafo de Arquímedes en acción

Elipsógrafo de Arquímedes. Versión de Gastón Tissandier (1896)

Elipsógrafo de madera (hacia 1900), conservado en los archivos de la Institución Smithsoniana

Elipsógrafo de bronce exhibido en el Museo de Historia de la Ciencia de la Ciudad de Ginebra

Según Dominique Raynaud, la atribución de este elipsógrafo a Arquímedes es infundada.[1] En ocasiones se le atribuye a Proclo,[2] porque este geómetra griego cita la propiedad utilizada en su comentario de Euclides.[1] Su construcción por el Marqués de L'Hôpital está atestiguada en 1707:[1] el Museo Galileo de Florencia posee un ejemplar datado en esta fecha.[3]

Este elipsógrafo se basa en la siguiente propiedad: si se considera un segmento [AD] de longitud a y un punto C sobre el segmento [AD] tales que AC=b, el lugar geométrico de los puntos A cuando los puntos C y D se mueven respectivamente sobre dos rectas perpendiculares es una elipse de semiejes a y b.

En efecto, si se denomina θ al ángulo ${\displaystyle ({\vec {i}},{\overrightarrow {CA}})}$, las coordenadas (x,y) del punto A cumplen las condiciones:

${\displaystyle y=CA\sin(\theta )}$

${\displaystyle x=DA\cos(\theta )}$

que definen la ecuación parametrizada de una elipse.

Los ejes no tienen por qué ser perpendiculares para dibujar una elipse.[4]

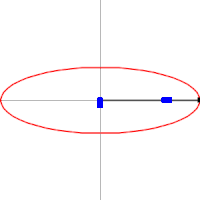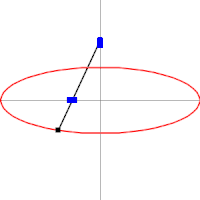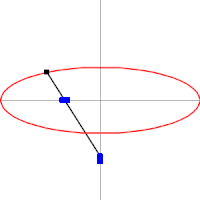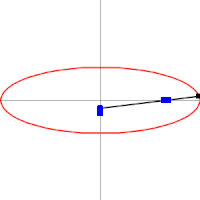
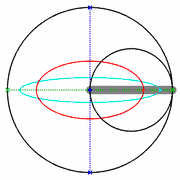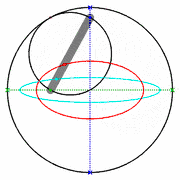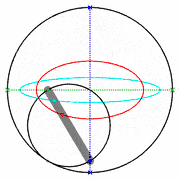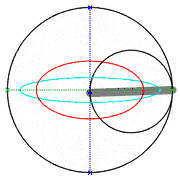
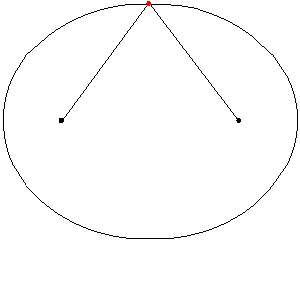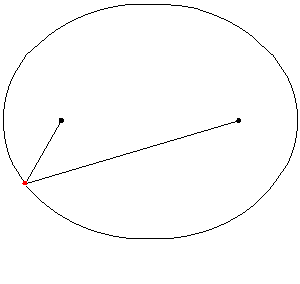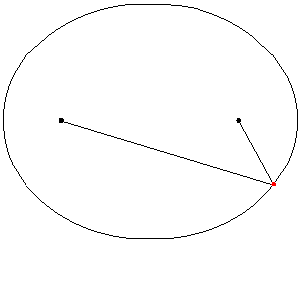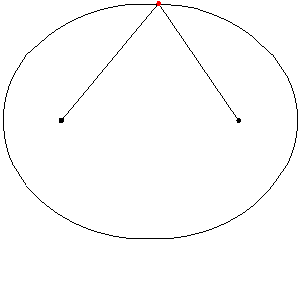
A medida que las lanzaderas se mueven de un lado a otro, cada una en su canal, todos los puntos de la barra se mueven en trayectorias elípticas. El movimiento de la barra se denomina movimiento elíptico. Los semiejes a y b de las elipses tienen longitudes iguales a las distancias desde el punto de la barra hasta cada uno de los dos pivotes.

Las rectas descritas por los pivotes son casos especiales de una elipse, en los que la longitud de un eje es el doble de la distancia entre los pivotes y la del otro es cero. Todos los puntos en un círculo con un diámetro definido por los dos pivotes se mueven alternativamente en tales líneas rectas. Este círculo corresponde al círculo más pequeño en un Acople Tusi.

El punto a mitad de camino entre los pivotes orbita en un círculo alrededor del punto donde se cruzan los canales. Este círculo es también un caso especial de elipse. Aquí los ejes son de igual longitud. El diámetro del círculo es igual a la distancia entre los pivotes. La dirección de viaje alrededor de la órbita es opuesta al sentido de rotación del mecanismo. Por lo tanto, si se usa una manivela centrada en el punto de cruce de los canales para impulsar la barra, la rotación de la muñequilla y la barra son iguales y opuestas, lo que en aplicaciones prácticas resulta en una fricción adicional. Esto se ve agravado por las altas fuerzas debidas al recorrido corto de la manivela de solo 1/4 del recorrido de los pivotes.

Es un ejemplo de un mecanismo de cuatro barras con dos deslizaderas y dos pivotes, un caso especial del mecanismo oblicuo más general. Como ya se ha indicado, los ejes que limitan los pivotes no tienen por qué ser perpendiculares y los puntos A, B y C pueden formar un triángulo, y el lugar geométrico resultante de C sigue siendo una elipse.[5]

Concepto

Mecanismo de Arquímedes Mecanismo de Arquímedes   Diagrama Diagrama   Lugares geométricos de algunos puntos a lo largo y más allá de un mecanismo de Arquímedes. En verde, el círculo descrito por el punto medio – en el fichero SVG, mover el puntero sobre el diagrama para mover el mecanismo Lugares geométricos de algunos puntos a lo largo y más allá de un mecanismo de Arquímedes. En verde, el círculo descrito por el punto medio – en el fichero SVG, mover el puntero sobre el diagrama para mover el mecanismo   Mecanismo de Arquímedes con tres lanzaderas Mecanismo de Arquímedes con tres lanzaderas

Gastón Tissandier ideó una versión simple de tal elipsógrafo:[6] todo lo que se necesita es un simple cuadrado y una regla en la que se ha practicado una ranura (B); la regla está equipada con una punta (A) y dos tornillos deslizantes (C y D). Se colocan los tornillos de manera que AC=b y AD=a, luego se gira la regla para que los tornillos queden siempre en contacto con los lados del cuadrado, y la punta con el trazador dibuja entonces la elipse de semiejes a y b, después de repetir la operación cuatro veces con la regla (una para cada arco).

Principio del círculo elipsográfico de Rohn

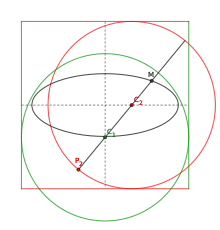
La realización práctica de elipses por este método tiene dos inconvenientes:

• El sistema de guiado de los puntos C y D genera imprecisiones que pueden conducir a un trazado inexacto.
• Este mismo sistema de guiado corre el riesgo de bloquear el dibujo de la elipse con el lápiz, forzar el dibujo de la elipse a trozos, o incluso impedir cualquier dibujo en el caso de elipses muy estrechas.

Círculo elipsográfico de Rohn (realización)

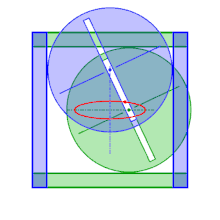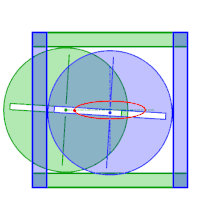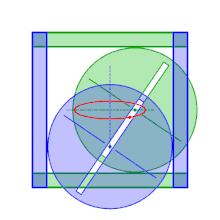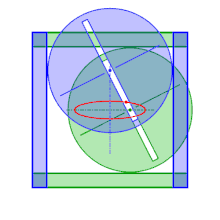
Por eso, sobre el mismo principio, se han construido elipsógrafos donde los puntos C y D se mantienen sobre los ejes indirectamente: los puntos en cuestión se convierten en los centros de círculos del mismo radio guiados por un marco externo. Uno de los círculos está limitado por los dos lados opuestos de un cuadrado, mientras que el otro círculo está limitado por los otros dos lados. El centro de uno de los círculos, por lo tanto, evoluciona sobre una mediana del cuadrado mientras que el otro evoluciona sobre la otra mediana. Los dos círculos comparten el mismo diámetro (estriado) y se fijan mediante tuercas para que la distancia entre los centros sea constante. Así, para dibujar una elipse con semiejes mayores a y b (inferior al medio lado del marco), basta con colocar el palpador a una distancia a del centro de uno de los círculos, y el segundo círculo se coloca fijado de tal manera que la distancia desde su centro hasta el trazador sea igual a b.

Sobre este modelo se construyen el elipsógrafo de Farey,[7] el Ellipsenzirkel de Karl Rohn[8] y el elipsógrafo HAFF.[9]

Otra técnica para fijar la posición de los puntos en los ejes del marco consiste en utilizar el acople Tusi (o par de al-Tusi) haciendo rodar un círculo de radio R dentro de un círculo de radio 2R. Entonces, cualquier punto vinculado al círculo pequeño describe una elipse. Uno de esos modelos está en exhibición en Museo de la Ciencia de Múnich.

Principio de La Hire Principio de La Hire  Elipsógrafo - Deutsches Museum Elipsógrafo - Deutsches Museum

Frans van Schooten, matemático holandés del siglo XVII, dedicó un libro entero a la construcción de secciones cónicas, De Organica Conicarum Sectionum (1646). Retomó el principio expuesto por Proclo para generalizarlo a cualquier punto de la recta y propuso un sistema articulado. También ideó otros dos mecanismos en forma de antiparalelogramo y rombo.

Principio del elipsógrafo de Van Schooten

El principio completa al de Arquímedes: si se considera un segmento [AB] de longitud a+b y un punto M sobre el segmento [AB] tal que AM=b, el lugar geométrico de los puntos M cuando los puntos A y B se mueven respectivamente sobre dos rectas perpendiculares es una elipse de semiejes a y b.

En efecto, si el punto M tiene coordenadas (x,y), el teorema de Pitágoras asegura que

${\displaystyle OA^{2}+OB^{2}=AB^{2}}$

es decir

${\displaystyle {\frac {OA^{2}}{AB^{2}}}+{\frac {OB^{2}}{AB^{2}}}=1}$

Sin embargo, según el teorema de Thales,

${\displaystyle {\frac {OA}{AB}}={\frac {x}{a}}}$

${\displaystyle {\frac {OB}{AB}}={\frac {y}{b}}}$

Entonces

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

Es la ecuación característica de la elipse de centro O y semiejes a y b. Esto asegura que el punto M está en efecto en esta elipse.

Por el contrario, si M es un punto de la elipse, si se denomina B al punto situado sobre el eje de ordenadas, en el mismo cuadrante que M, y tal que BM=a, y si A es el punto de intersección de (BM) y el eje de abscisas, se demuestra fácilmente, por un razonamiento análogo al anterior, que MA=b

El elipsógrafo de Van Schooten[10] simplifica el proceso al considerar un sistema articulado OIA en el que

${\displaystyle OI=IA={\frac {a+b}{2}}}$

El punto O es fijo, el punto A se mueve en línea recta y arrastra a los puntos I y M.[3]

Principio del elipsógrafo con un antiparalelogramo

Elipsógrafo con un antiparalelogramo (animación)

Este elipsógrafo, el segundo presentado por van Schooten,[11] utiliza un polígono articulado, un antiparalelogramo que consiste en un cuadrilátero con dos de sus lados opuestos cruzados F₁ABF₂, y cuyos lados son iguales dos a dos. Para dibujar la elipse de eje mayor 2a y cuya distancia entre los focos es 2c, basta tomar

${\displaystyle F_{1}F_{2}=AB=2c}$

${\displaystyle F_{1}A=F_{2}B=2a}$

Los vértices F₁ y F₂ están fijos en los focos de la elipse. Cuando la rama F₁A gira alrededor de F₁, la rama BF₂ gira alrededor de F₂ y el antiparalelogramo se deforma. El punto de intersección M de las dos ramas atraviesa entonces la elipse buscada. De hecho, las propiedades de simetría del antiparalelogramo aseguran que

${\displaystyle MF_{2}=MA}$

y que

${\displaystyle F_{1}M+MA=F_{1}A=2a}$

Entonces

${\displaystyle F_{1}M+MF_{2}=2a}$

Esta es la definición bifocale de la elipse, también utilizada en el método del jardinero.

Elipsógrafo de van Schooten (1646)

Principio del elipsógrafo con un círculo directriz

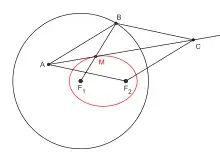
Este elipsógrafo utiliza un rombo articulado de cualquier tamaño ABCF₂, equipado con una varilla deslizante [AC) y una barra F₁B de longitud 2a. Los puntos F₁ y F₂ están fijos en los focos de la elipse que se quiere trazar y la barra F₁B que pivota alrededor de F₁ arrastra al rombo que se deforma. Las barras F₁B y AC se encuentran en M, que describe la elipse con focos F₁ y F₂ y eje mayor 2a.

En efecto, este mecanismo permite determinar, para cada posición de B sobre la circunferencia directriz de la elipse, el centro de la circunferencia que pasa por F₂ y es tangente a la circunferencia directriz en B: este centro está situado en la bisectriz perpendicular de [BF₂] que resulta ser la diagonal (AC), y sobre el segmento F₁B. El centro de este círculo es efectivamente el punto M. Sin embargo, se sabe que el conjunto de estos centros dibuja la elipse deseada (véase construcción de la elipse mediante un círculo directriz).

Esta herramienta también permite especificar en cada punto la posición de la tangente a la elipse materializada aquí por la línea recta (AC). De hecho, la propriedad de reflexividad de la elipse asegura que la tangente es la bisectriz exterior del ángulo F₁MF₂. En consecuencia, la recta (AC), eje de simetría del rombo, es la bisectriz del ángulo BMF₂, y por lo tanto, la bisectriz exterior del ángulo F₁MF₂.

Van Schooten demuestra cómo se puede utilizar este instrumento para dibujar elipses,[12] pero también para trazar hipérbolas[13] y parábolas.[14]

Principio del elipsógrafo de Delaunay

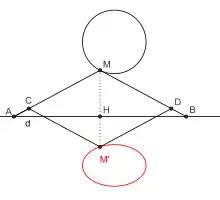
El elipsógrafo de Delaunay, descrito por Nikolái Delaunay en 1895,[15] utiliza un sistema articulado que permite construir la imagen de una figura por una afinidád, o bien, lo que es equivalente, la imagen de una figura por proyección de un plano en otro plano.

En la figura opuesta, los puntos A y B se deslizan hacia la derecha (d). Los brazos MA y MB tienen la misma longitud y CMDM' es un diamante articulado. El punto M' es entonces la imagen del punto M en la afinidad ortogonal del eje (d) y con relación ${\displaystyle -{\frac {AM-2AC}{AM}}}$

En efecto, la recta (MM') corta ortogonalmente al eje (d) en H y la presencia de triángulos semejantes permite establecer la siguiente igualdad de razones:

${\displaystyle {\frac {MH}{MA}}={\frac {M'H}{MA-2AC}}}$

o también

${\displaystyle {\frac {M'H}{MH}}={\frac {MA-2AC}{MA}}}$

La elipse con semiejes a y b, siendo la imagen de un círculo de radio a por una afinidad de razón b/a, puede ser construida por el elipsógrafo siempre que ${\displaystyle {\frac {MA-2AC}{MA}}={\frac {b}{a}}}$: cuando el punto M pasa por el círculo de radio a, su imagen M' atraviesa la elipse buscada.

Principio del elipsógrafo de Kopp (1993)

Este elipsógrafo, patentado por Franz Otto Kopp en 1993,[16] permite dibujar pero también recortar elipses.[17] Consta de dos ruedas dentadas del mismo radio y un pantógrafo. Dos de los puntos del pantógrafo (A y B) están fijados en las ruedas dentadas, en puntos ligeramente excéntricos. El tercer punto (M) dibuja entonces una elipse cuando una de las ruedas dentadas gira, impulsando a su vecina.

La demostración matemática de esta propiedad se puede hacer fácilmente usando la representación paramétrica compleja de la elipse. En el sistema de coordenadas con centro C y eje (d)=(CC_b), los afijos de los puntos A y B se pueden expresar mediante el ángulo θ, las distancias ${\displaystyle C_{b}B=r_{b}}$ y ${\displaystyle C_{a}A=r_{a}}$, el radio r de las dos ruedas y el desfase α entre las dos ruedas

${\displaystyle z_{B}=r+r_{b}\mathrm {e} ^{\mathrm {i} \theta }}$

${\displaystyle z_{A}=-r+r_{a}\mathrm {e} ^{\mathrm {i} (\alpha -\theta )}}$

Según el principio del pantógrafo, existe una constante k tal que AM=kAB, por lo que el afijo de M viene determinado por

${\displaystyle z_{M}=kz_{B}+(1-k)z_{A}=(2k-1)r+kr_{b}\mathrm {e} ^{\mathrm {i} \theta }+(1-k)r_{a}\mathrm {e} ^{\alpha -\mathrm {i} \theta }}$

Si ahora se sitúa el puntero en el marco de referencia de centro O con el afijo (2k-1)r (es la imagen del centro C_b en la prolongación del centro C_a y relación k) y del eje (d') formando con (d) un ángulo de α/2, el punto M tiene por afijo

${\displaystyle z'_{M}=kr_{b}\mathrm {e} ^{\mathrm {i} (\theta -\alpha /2)}+(1-k)r_{a}\mathrm {e} ^{\mathrm {i} (\alpha /2-\theta )}}$

que es la ecuación paramétrica de la elipse de centro O, eje (d') y semiejes

${\displaystyle a=kr_{b}+(k-1)r_{a}}$

${\displaystyle b=|kr_{b}-(k-1)r_{a}|}$

Para dibujar la elipse de semiejes a y b basta con colocar A y B de manera que[18]

${\displaystyle r_{b}={\frac {a+b}{2k}}}$

${\displaystyle r_{a}={\frac {a-b}{2(k-1)}}}$

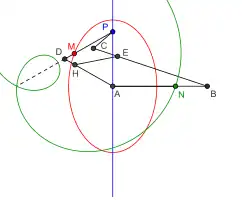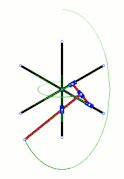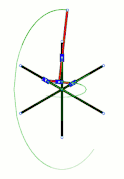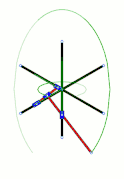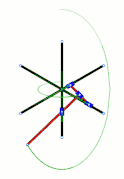
Elipsógrafo de Darboux Breguet: AD=DP=a; PC=CE=ka; CB=a/k; AB=a/k-ka; AH=HE=a-k²a. Cuando A y B están fijos, P describe un segmento y M una elipse. Cuando D y P están fijos, N describe una porción del caracol de Pascal

Los matemáticos también han buscado instrumentos que puedan dibujar otras curvas además de las elipses. Así, en 1818, el mecánico Joseph Clement recibió la medalla de oro de la Royal Society of Arts[19] por la construcción de un aparato que no solo construía elipses mediante un mecanismo análogo al de Arquímedes o Van Schooten,[20] sino que también generaba círculos, paralelas y espirales; y además los recortaba para obtener secciones regulares.[21]

En el caso de los polígonos articulados, se buscaba disminuir el número de ramas y aumentar el número de funcionalidades. Sobre este tema se puede citar el elipsógrafo descrito en 1879 por Jean Gaston Darboux y construido por Breguet,[22] inspirado en el trazador ideado por Harry Hart.[23] Se trata de un pentágono articulado restringido para dibujar perpendiculares, elipses y caracoles de Pascal.[22]

Cinco puntos son suficientes para determinar una cónica. La aplicación del teorema de Pascal proporciona un método para construir la cónica en cuestión. Establece que, para cualquier hexágono cuyos vértices estén sobre la cónica, los puntos de intersección de lados opuestos[24] están alineados:

• Los 5 puntos conocidos de la cónica permiten construir una trayectoria poligonal formada por los segmentos a₁, a₂, a₃, a₄;
• Las líneas rectas que incluyen a a₁ y a₄ se cruzan en I;
• Un 6° punto M de la cónica permitiría continuar la poligonal por el segmento a₅ que debe encontrarse con a₂ en un punto J que se elige arbitrariamente sobre la recta que incluye a a₂;
• El segmento a₆ que cierra la poligonal debe encontrarse con a₃ en un punto K alineado con I y J. El punto K está por tanto en la intersección de (IJ) y la recta que incluye a a₃;
• El punto M correspondiente a J está en el punto de encuentro de las líneas rectas A₁K y A₅J.

Este principio se puede materializar en un sistema articulado formado por 2 brazos fijos y 3 brazos deslizantes y pivotantes:

• Se colocan ventosas en los 5 puntos de la cónica ya presentes, así como en el punto I;
• Los dos brazos fijos siguen los segmentos a₂ y a₃;
• Dos de los brazos móviles se encuentran en J, punto móvil del brazo fijo que incluye a a₂, uno de los brazos pasa por I y el otro por A₅;
• El brazo que pasa por I se encuentra con el brazo fijo que incluye a a₃ en K;
• Se coloca un sistema deslizante en K y en su interior se inserta un brazo que pivotará alrededor de A₁;
• Los brazos que pasan por A₁ y A₅ se encuentran en M donde se coloca un trazador que atravesará la elipse.

Se encuentra un sistema análogo en el caso de que entre los cinco puntos que definen la elipse haya dos puntos dobles, como en un modelo desarrollado por Friedrich Schilling,[25] expuesto en la colección de modelos e instrumentos matemáticos de la Universidad de Gotinga.[26]