Experimento de la doble rendija

En la física moderna, el experimento de la doble rendija es una demostración de que la luz y la materia pueden mostrar características tanto de ondas como de partículas definidas clásicamente; además, muestra la naturaleza fundamentalmente probabilística de los fenómenos de la mecánica cuántica. Este tipo de experimento fue realizado por primera vez, utilizando luz, por Thomas Young en 1801,[1] como demostración del comportamiento ondulatorio de la luz.[2] En aquella época se pensaba que la luz consistía en ondas o en partículas. Con el inicio de la física moderna, unos cien años más tarde, se comprendió que la luz podía, de hecho, mostrar un comportamiento característico tanto de las ondas como de las partículas. En 1927, Davisson y Germer demostraron que los electrones muestran el mismo comportamiento, lo que se extendió posteriormente a los átomos y las moléculas.[3][4] El experimento de Thomas Young con la luz formaba parte de la física clásica mucho antes del desarrollo de la mecánica cuántica y del concepto de dualidad onda-partícula. Él creía que demostraba que la teoría ondulatoria de la luz era correcta, y su experimento se conoce a veces como el experimento de Young o las rendijas de Young.[5]

Los fotones o partículas de materia (como un electrón) producen un patrón de onda cuando se usan dos rendijas

El forma parte a una clase general de experimentos de "doble trayectoria", en los que una onda se divide en dos ondas separadas (la onda suele estar formada por muchos fotones y es mejor denominarla frente de onda (no confundirla con las propiedades ondulatorias del fotón individual) que posteriormente se combinan en una sola onda. Los cambios en las longitudes de trayectoria de ambas ondas dan lugar a un desplazamiento de fase, creando un patrón de interferencia. Otra versión es el interferómetro Mach-Zehnder, que divide el haz con un divisor de haz.

En la versión básica de este experimento, una fuente de luz coherente, como un rayo láser, ilumina una placa perforada por dos rendijas paralelas, y la luz que pasa por las rendijas se observa en una pantalla detrás de la placa.[6][7] La naturaleza ondulatoria de la luz hace que las ondas luminosas que pasan por las dos rendijas interfieran, produciendo bandas brillantes y oscuras en la pantalla, un resultado que no se esperaría si la luz estuviera formada por partículas clásicas.[6][8] Sin embargo, la luz siempre se absorbe en la pantalla en puntos discretos, como partículas individuales (no ondas); el patrón de interferencia aparece a través de la densidad variable de estos impactos de partículas en la pantalla.[9] Además, las versiones del experimento que incluyen detectores en las rendijas encuentran que cada fotón detectado pasa a través de una rendija (como lo haría una partícula clásica), y no a través de ambas rendijas (como lo haría una onda).[10][11][12][13][14] Sin embargo, estos experimentos demuestran que las partículas no forman el patrón de interferencia si se detecta por qué rendija pasan. Estos resultados demuestran el principio de la dualidad onda-partícula.[15][16]

Se ha comprobado que otras entidades a escala atómica, como los electrones, presentan el mismo comportamiento cuando se disparan hacia una doble rendija.[7] Además, se observa que la detección de impactos discretos individuales es inherentemente probabilística, lo cual es inexplicable utilizando la mecánica clásica.[7]

El experimento puede realizarse con entidades mucho mayores que los electrones y los fotones, aunque resulta más difícil a medida que aumenta el tamaño. Las entidades más grandes con las que se ha realizado el experimento de la doble rendija han sido moléculas compuestas por 2.000 átomos cada una (cuya masa total era de 25.000 unidades de masa atómica).[17]

El experimento de la doble rendija (y sus variaciones) se ha convertido en un clásico por su claridad a la hora de expresar los enigmas centrales de la mecánica cuántica. Debido a que demuestra la limitación fundamental de la capacidad del observador para predecir los resultados experimentales, Richard Feynman lo llamó "un fenómeno que es imposible [...] de explicar de cualquier manera clásica, y que tiene en él el corazón de la mecánica cuántica. En realidad, contiene el único misterio [de la mecánica cuántica]."[7]

Relevancia física

Acumulación de electrones con el paso del tiempo.

Aunque este experimento se presenta habitualmente en el contexto de la mecánica cuántica, fue diseñado mucho antes de la llegada de esta teoría para responder a la pregunta de si la luz tenía una naturaleza corpuscular o si, más bien, consistía en ondas viajando por el éter, análogamente a las ondas sonoras viajando en el aire. La naturaleza corpuscular de la luz está basada sobre todo en las investigaciones, descubrimientos y trabajos de Newton; la naturaleza ondulatoria, en los trabajos clásicos de Hooke y Huygens.

Los patrones de interferencia observados por estos científicos restaban crédito a la teoría corpuscular. La teoría ondulatoria se mostró muy robusta hasta los comienzos del siglo XX, cuando nuevos experimentos empezaron a mostrar un comportamiento que solo podía ser explicado por una naturaleza corpuscular de la luz. De este modo el experimento de la doble rendija y sus múltiples variantes se convirtieron en un experimento clásico por su claridad a la hora de presentar una de las principales características de la mecánica cuántica.

La forma en la que se presenta normalmente el experimento no se realizó hasta 1961 utilizando electrones y mostrando la dualidad onda-corpúsculo de las partículas subatómicas (Claus Jönsson, Zeitschrift für Physik, 161, 454; Electron diffraction at multiple slits, American Journal of Physics, 42, 4-11, 1974). En 1974 fue posible realizar el experimento en su forma más ambiciosa, electrón a electrón, comprobando las hipótesis mecanocuánticas predichas por Richard Feynman. Este experimento fue realizado por un grupo italiano liderado por Pier Giorgio Merli y repetido de manera concluyente en 1989 por un equipo japonés liderado por Akira Tonomura y que trabajaba para la compañía Hitachi. El experimento de la doble rendija electrón a electrón se explica a partir de la interpretación probabilística de la trayectoria seguida por las partículas.

El experimento

Formulación clásica

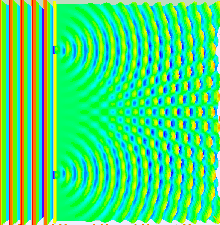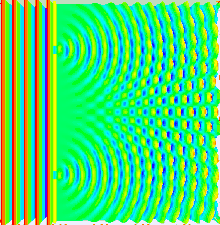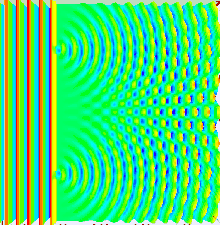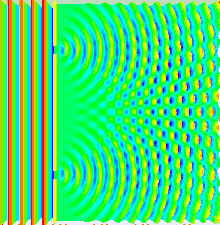
Dos patrones de difracción por una onda plana.

Dos ranuras están iluminadas por una onda plana.

La formulación original de Young es muy diferente de la moderna formulación del experimento y utiliza una doble rendija. En el experimento original un estrecho haz de luz, procedente de un pequeño agujero en la entrada de la cámara, es dividido en dos por una tarjeta de una anchura de unos 0,2 mm. El haz de luz tenía una anchura ligeramente superior al ancho de la tarjeta divisoria por lo que cuando esta se posicionaba correctamente el haz era dividido en dos, cada uno pasando por un lado distinto de la pared divisoria. El resultado puede verse proyectado sobre una pared en una habitación oscurecida. Young realizó el experimento en la misma reunión de la Royal Society mostrando el patrón de interferencias producido demostrando la naturaleza ondulatoria de la luz.

El mismo conjunto de doble rendija (0,7 mm entre las rendijas); en la imagen superior, una rendija está cerrada. En la imagen de una sola rendija, se forma un patrón de difracción (los puntos débiles a ambos lados de la banda principal) debido al ancho distinto de cero de la rendija. También se ve un patrón de difracción en la imagen de doble rendija, pero con el doble de intensidad y con la adición de muchas franjas de interferencia más pequeñas.

Formulación moderna

La formulación moderna permite mostrar tanto la naturaleza ondulatoria de la luz como la dualidad onda-corpúsculo de la materia. En una cámara oscura se deja entrar un haz de luz por una rendija estrecha. La luz llega a una pared intermedia con dos rendijas. Al otro lado de esta pared hay una pantalla de proyección o una placa fotográfica. Cuando una de las rejillas se cubre aparece un único pico correspondiente a la luz que proviene de la rendija abierta. Sin embargo, cuando ambas están abiertas en lugar de formarse una imagen de superposición de las obtenidas con las rendijas abiertas individualmente, se obtiene una figura de interferencias con rayas oscuras y otras brillantes.

Este patrón de interferencias se explica fácilmente a partir de la interferencia de las ondas de luz, al combinarse la luz que procede de dos rendijas, de manera muy similar a como las ondas en la superficie del agua se combinan para crear picos y regiones más planas. En las líneas brillantes la interferencia es de tipo "constructiva". El mayor brillo se debe a la superposición de ondas de luz coincidiendo en fase sobre la superficie de proyección. En las líneas oscuras la interferencia es "destructiva" con prácticamente ausencia de luz a consecuencia de la llegada de ondas de luz de fase opuesta (la cresta de una onda se superpone con el valle de otra).

Variaciones del experimento

Interferencia de partículas individuales

Acumulación del patrón de interferencia de las detecciones de partículas individuales.

Una versión importante de este experimento incluye partículas individuales. Al enviar las partículas a través de un aparato de doble rendija de una en una, aparecen partículas individuales en la pantalla, como era de esperar. Sin embargo, es sorprendente que aparezca un patrón de interferencia cuando se permite que estas partículas se acumulen una a una (véase la imagen adyacente). Esto demuestra la dualidad onda-partícula, que afirma que toda la materia presenta propiedades tanto de onda como de partícula: La partícula se mide como un solo pulso en una sola posición, mientras que la onda describe la probabilidad de absorber la partícula en un lugar específico de la pantalla.[18] Se ha demostrado que este fenómeno ocurre con los fotones y los electrones,[19] átomos, e incluso algunas moléculas. El éxito se alcanzó con el buckminsterfullereno (C
60) en 2001,[20][21][22] con 2 moléculas de 430 átomos (C
60(C
12F
25)
10 y C
168H
94F
152O
8N
4S
4) en 2011,[23] y con moléculas de hasta 2000 átomos en 2019.[24]

La probabilidad de detección es el cuadrado de la amplitud de la onda y puede calcularse con ondas clásicas (véase abajo). Desde el origen de la mecánica cuántica, algunos teóricos han buscado formas de incorporar determinantes adicionales o "variables ocultas" que, si se conocieran, darían cuenta de la ubicación de cada impacto individual con el objetivo.[25]

Intereferencia con antimateria

La interferencia de partículas individuales de antimateria fue demostrada por primera vez con un experimento análogo al de la doble rendija en 2018 con positrones en el Laboratorio Positrones (L-NESS, Politecnico di Milano) de Rafael Ferragut en Como, Italia, por un grupo liderado por Marco Giammarchi.[26] Para ello se utilizó un interferómetro Talbot-Lau de aumento periódico basado en rendijas materiales de difracción. Las franjas resultantes fueron detectadas mediante emulsiones nucleares capaces de determinar el punto de impacto de cada positrón individual con resolución submicrométrica.

Interferómetro Mach-Zehnder

Los fotones en un interferómetro de Mach-Zehnder muestran una interferencia similar a la de las ondas y una detección similar a la de las partículas en detectores de un solo fotón.

El interferómetro de Mach-Zehnder puede considerarse como una versión simplificada del experimento de la doble rendija. En lugar de propagarse por el espacio libre después de las dos rendijas y alcanzar cualquier posición en una pantalla extendida, en el interferómetro los fotones sólo pueden propagarse por dos caminos y alcanzar dos fotodetectores discretos. Esto permite describirlo mediante álgebra lineal simple en dimensión 2, en lugar de ecuaciones diferenciales.

Un fotón emitido por el láser choca con el primer divisor de haz y se encuentra entonces en una superposición entre las dos trayectorias posibles. En el segundo divisor de haz estos caminos interfieren, haciendo que el fotón golpee el fotodetector de la derecha con probabilidad uno, y el fotodetector de la parte inferior con probabilidad cero. Es interesante considerar lo que sucedería si el fotón estuviera definitivamente en cualquiera de los caminos entre los divisores de haz. Esto se puede conseguir bloqueando uno de los caminos, o de forma equivalente, detectando la presencia de un fotón allí. En ambos casos ya no habrá interferencia entre los caminos, y ambos fotodetectores serán alcanzados con probabilidad 1/2. De esto podemos concluir que el fotón no toma un camino u otro después del primer divisor de haz, sino que se encuentra en una auténtica superposición cuántica de los dos caminos.[27]

Los experimentos "de ida" y el principio de complementariedad

Un conocido experimento mental predice que si se colocan detectores de partículas en las rendijas, mostrando por qué rendija pasa un fotón, el patrón de interferencia desaparecerá.[7] Este experimento ilustra el principio de complementariedad, según el cual los fotones pueden comportarse como partículas o como ondas, pero no pueden ser observados como ambas cosas a la vez.[28][29][30] A pesar de la importancia de este experimento mental en la historia de la mecánica cuántica (por ejemplo, véase la discusión sobre la versión de Einstein de este experimento), no se propusieron realizaciones técnicamente viables de este experimento hasta la década de 1970.[31] (Las implementaciones ingenuas del experimento mental del libro de texto no son posibles porque los fotones no pueden ser detectados sin absorber el fotón). En la actualidad, se han realizado múltiples experimentos que ilustran diversos aspectos de la complementariedad.[32]

Un experimento realizado en 1987[33][34] produjo resultados que demostraron que se podía obtener información sobre el camino que había seguido una partícula sin destruir la interferencia por completo. Esto demostró el efecto de las mediciones que perturbaban las partículas en tránsito en menor grado y, por lo tanto, influían en el patrón de interferencia sólo en una medida comparable. En otras palabras, si no se insiste en que el método utilizado para determinar por qué rendija pasa cada fotón sea completamente fiable, se puede seguir detectando un patrón de interferencia (degradado).[35]

Elección retardada y variaciones del borrador cuántico

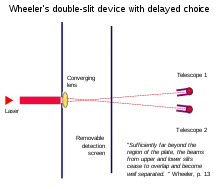
Un diagrama del experimento de elección retardada de Wheeler, que muestra el principio de determinación de la trayectoria del fotón después de pasar por la rendija.

Los experimentos de elección retardada de Wheeler demuestran que la extracción de información sobre "qué camino" después de que una partícula pase por las rendijas puede parecer que altera retroactivamente su comportamiento anterior en las rendijas.

Los experimentos del borrador cuántico demuestran que el comportamiento de las ondas puede restaurarse borrando o haciendo que no esté disponible de forma permanente la información de "qué camino".

En un artículo de la revista Scientific American se ofrece una sencilla ilustración casera del fenómeno del borrador cuántico.[36] Si se colocan polarizadores antes de cada rendija con sus ejes ortogonales entre sí, se eliminará el patrón de interferencia. Se puede considerar que los polarizadores introducen información sobre la trayectoria de cada haz. La introducción de un tercer polarizador delante del detector con un eje de 45° respecto a los otros polarizadores "borra" esta información, permitiendo que el patrón de interferencia vuelva a aparecer. Esto también puede explicarse considerando que la luz es una onda clásica,[36]^: 91 y también cuando se utilizan polarizadores circulares y fotones individuales.[37]^: 6 Las implementaciones de los polarizadores que utilizan pares de fotones entrelazados no tienen una explicación clásica.[37]

Formulación clásica de óptica de onda

Foto de la interferencia de doble rendija de la luz solar.

Gran parte del comportamiento de la luz se puede modelar utilizando la teoría de ondas clásica. El principio de Huygens-Fresnel es uno de esos modelos; establece que cada punto en un frente de onda genera una ondícula secundaria, y que la perturbación en cualquier punto posterior se puede encontrar sumando las contribuciones de las ondículas individuales en ese punto. Esta suma debe tener en cuenta la fase y la amplitud de las ondículas individuales. Solo se puede medir la intensidad de un campo de luz; esto es proporcional al cuadrado de la amplitud.

En el experimento de doble rendija, las dos rendijas se iluminan con un solo rayo láser. Si el ancho de las rendijas es lo suficientemente pequeño (menor que la longitud de onda de la luz láser), las rendijas difractan la luz en ondas cilíndricas. Estos dos frentes de onda cilíndricos se superponen, y la amplitud, y por lo tanto la intensidad, en cualquier punto de los frentes de onda combinados depende tanto de la magnitud como de la fase de los dos frentes de onda. La diferencia de fase entre las dos ondas está determinada por la diferencia en la distancia recorrida por las dos ondas.

Si la distancia de visualización es grande en comparación con la separación de las rendijas (el campo lejano), la diferencia de fase se puede encontrar utilizando la geometría que se muestra en la figura a la derecha a continuación. La diferencia de ruta entre dos ondas que viajan en un ángulo θ viene dada por:

d\sin \theta \approx d\theta

Donde d es la distancia entre las dos rendijas. Cuando las dos ondas están en fase, es decir, la diferencia de trayectoria es igual a un número integral de longitudes de onda, la amplitud sumada y, por lo tanto, la intensidad sumada es máxima, y cuando están en antifase, es decir, la diferencia de trayectoria es igual a la mitad una longitud de onda, una longitud de onda y media, etc., luego las dos ondas se cancelan y la intensidad sumada es cero. Este efecto se conoce como interferencia. Los máximos de franja de interferencia ocurren en ángulos

~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots

donde λ es la longitud de onda de la luz. La separación angular de las franjas, $θ f$ , viene dada por

\theta _{f}\approx \lambda /d

La separación de las franjas a una distancia z de las rendijas viene dada por

~w=z\theta _{f}=z\lambda /d

Por ejemplo, si dos ranuras están separadas por 0,5 mm (d) y se iluminan con un láser de longitud de onda de 0.6 μm (λ), entonces a una distancia de 1 m (z), la separación de las franjas será de 1,2 mm.

Si el ancho de las rendijas b es mayor que la longitud de onda, la ecuación de difracción de Fraunhofer da la intensidad de la luz difractada como:[38]

{\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi b\sin \theta }{\lambda }}\right]\end{aligned}}

Donde la función sinc se define como sinc(x) = sin(x)/x for x ≠ 0, y sinc(0) = 1.

Esto se ilustra en la figura anterior, donde el primer patrón es el patrón de difracción de una sola rendija, dada por la función sinc en esta ecuación, y la segunda figura muestra la intensidad combinada de la luz difractada de las dos rendijas, donde el cos la función representa la estructura fina, y la estructura más gruesa representa la difracción por las rendijas individuales como se describe en la función sinc.

Se pueden hacer cálculos similares para el campo cercano utilizando la ecuación de difracción de Fresnel. A medida que el plano de observación se acerca al plano en el que se ubican las rendijas, los patrones de difracción asociados con cada rendija disminuyen de tamaño, de modo que el área en la que ocurre la interferencia se reduce y puede desaparecer por completo cuando no hay superposición en los dos patrones difractados.[39]

Interpretaciones del experimento

Al igual que el experimento de pensamiento del gato de Schrödinger, el experimento de la doble rendija a menudo se usa para resaltar las diferencias y similitudes entre las diversas interpretaciones de la mecánica cuántica.

Interpretación de Copenhague

La interpretación de Copenhague, presentada por algunos de los pioneros en el campo de la mecánica cuántica, afirma que no es deseable plantear nada que vaya más allá de las fórmulas matemáticas y los tipos de aparatos físicos y reacciones que nos permiten obtener algo de conocimiento de lo que sucede a escala atómica. Una de las construcciones matemáticas que permite a los experimentadores predecir con mucha precisión ciertos resultados experimentales a veces se denomina onda de probabilidad. En su forma matemática es análoga a la descripción de una onda física, pero sus "crestas" y "valles" indican niveles de probabilidad de que ocurran ciertos fenómenos (p. ej., una chispa de luz en cierto punto de la pantalla del detector) eso se puede observar en el macro mundo de la experiencia humana ordinaria.

Se puede decir que la "onda" de probabilidad "atraviesa el espacio" porque los valores de probabilidad que uno puede calcular a partir de su representación matemática dependen del tiempo. No se puede hablar de la ubicación de ninguna partícula, como un fotón, entre el momento en que se emite y el momento en que se detecta simplemente porque, para decir que algo se encuentra en algún lugar en un momento determinado, uno tiene que detectarlo. El requisito para la aparición eventual de un patrón de interferencia es que se emitan partículas y que haya una pantalla con al menos dos caminos distintos para que la partícula tome del emisor a la pantalla de detección. Los experimentos no observan nada entre el tiempo de emisión de la partícula y su llegada a la pantalla de detección. Si luego se realiza un trazado de rayos como si una onda de luz (como se entiende en la física clásica) sea lo suficientemente amplia como para tomar ambos caminos, entonces ese trazado de rayos predecirá con precisión la aparición de máximos y mínimos en la pantalla del detector cuando muchas partículas pasan a través del aparato y gradualmente "pintar" el patrón de interferencia esperado.

Formulación integral de ruta

Uno de un número infinito de rutas igualmente probables utilizadas en la integral de ruta de Feynman (ver también: proceso de Wiener)

La interpretación de Copenhague es similar a la formulación integral de la mecánica cuántica proporcionada por Feynman. La formulación integral del camino reemplaza la noción clásica de una trayectoria única para un sistema, con una suma sobre todas las trayectorias posibles. Las trayectorias se suman mediante el uso de la integración funcional.

Cada ruta se considera igualmente probable y, por lo tanto, aporta la misma cantidad. Sin embargo, la fase de esta contribución en cualquier punto dado a lo largo del camino está determinada por la acción a lo largo del camino:

A_{\text{camino}}(x,y,z,t)=e^{iS(x,y,z,t)}

Luego se suman todas estas contribuciones, y la magnitud del resultado final se eleva al cuadrado, para obtener la distribución de probabilidad para la posición de una partícula:

p(x,y,z,t)\propto \left\vert \int _{\text{todos los caminos}}e^{iS(x,y,z,t)}\right\vert ^{2}

Como siempre es el caso al calcular la probabilidad, los resultados deben normalizarse imponiendo:

\iiint _{\text{todo el espacio}}p(x,y,z,t)\,\mathrm {d} V=1

Para resumir, la distribución de probabilidad del resultado es el cuadrado normalizado de la norma de la superposición, sobre todas las rutas desde el punto de origen hasta el punto final, de ondas que se propagan proporcionalmente a la acción a lo largo de cada ruta. Las diferencias en la acción acumulativa a lo largo de los diferentes caminos (y, por lo tanto, las fases relativas de las contribuciones) producen el patrón de interferencia observado por el experimento de doble rendija. Feynman enfatizó que su formulación es simplemente una descripción matemática, no un intento de describir un proceso real que podamos medir.

Interpretación relacional

Un ejemplo del principio de incertidumbre relacionado con la interpretación relacional. Cuanto más se sabe de la posición de una partícula, menos se sabe de la velocidad, y viceversa

Según la interpretación relacional de la mecánica cuántica, propuesta por primera vez por Carlo Rovelli,[40] las observaciones como las del experimento de la doble rendija resultan específicamente de la interacción entre el observador (dispositivo de medición) y el objeto observado (con el que se interactúa físicamente), no de ninguna propiedad absoluta que posea el objeto. En el caso de un electrón, si se "observa" inicialmente en una rendija determinada, la interacción observador-partícula (fotón-electrón) incluye información sobre la posición del electrón. Esto limita parcialmente la ubicación final de la partícula en la pantalla. Si se "observa" (se mide con un fotón) no en una rendija concreta, sino en la pantalla, entonces no hay información sobre "qué camino" como parte de la interacción, por lo que la posición "observada" del electrón en la pantalla está determinada estrictamente por su función de probabilidad. Esto hace que el patrón resultante en la pantalla sea el mismo que si cada electrón individual hubiera pasado por ambas rendijas.

Interpretación de muchos mundos

El físico David Deutsch sostiene en su libro The Fabric of Reality que el experimento de la doble rendija es una prueba de la interpretación de muchos mundos. Sin embargo, dado que todas las interpretaciones de la mecánica cuántica son empíricamente indistintas, algunos científicos se muestran escépticos ante esta afirmación.

La teoría de De Broglie-Bohm

Una alternativa a la concepción estándar de la mecánica cuántica, la teoría de De Broglie-Bohm, afirma que las partículas también tienen ubicaciones precisas en todo momento, y que sus velocidades están definidas por la función de onda. Así, mientras que una sola partícula viajará a través de una rendija en particular en el experimento de la doble rendija, la llamada "onda piloto" que influye en ella viajará a través de ambas. Las trayectorias de las dos rendijas de Broglie-Bohm fueron calculadas por primera vez por Chris Dewdney mientras trabajaba con Chris Philippidis y Basil Hiley en el Birkbeck College (Londres).[41] La teoría de Broglie-Bohm produce los mismos resultados estadísticos que la mecánica cuántica estándar, pero prescinde de muchas de sus dificultades conceptuales.[42]

Trayectorias bohemias

Trayectorias de partículas bajo la teoría de De Broglie-Bohm en el experimento de la doble rendija.

100 trayectorias guiadas por la función de onda. En la teoría de De Broglie-Bohm, una partícula está representada, en todo momento, por una función de onda y una posición (centro de masa). Se trata de una especie de realidad aumentada en comparación con la interpretación estándar.

Simulación numérica del experimento de la doble rendija con electrones. Figura de la izquierda: evolución (de izquierda a derecha) de la intensidad del haz de electrones a la salida de las rendijas (izquierda) hasta la pantalla de detección situada 10 cm después de las rendijas (derecha). A mayor intensidad, mayor es el color azul claro - Figura del centro: impactos de los electrones observados en la pantalla - Figura de la derecha: intensidad de los electrones en la aproximación de campo lejano (en la pantalla). Datos numéricos del experimento de Claus Jönsson (1961). Los fotones, los átomos y las moléculas siguen una evolución similar.

Experimento original de Young

La paradoja del experimento

Esta paradoja trata de un experimento mental, un experimento ficticio no realizable en la práctica, que fue propuesto por Richard Feynman[43] examinando teóricamente los resultados del experimento de Young analizando el movimiento de cada fotón.

Para la década de 1920, numerosos experimentos (como el efecto fotoeléctrico, el efecto Compton y la producción de rayos X entre otros) habían demostrado que la luz interacciona con la materia únicamente en cantidades discretas, en paquetes "cuantizados" o "cuánticos" denominados fotones. Si la fuente de luz pudiera reemplazarse por una fuente capaz de producir fotones individualmente y la pantalla fuera suficientemente sensible para detectar un único fotón, el experimento de Young podría, en principio, producirse con fotones individuales con idéntico resultado.

Si una de las rendijas se cubre, los fotones individuales irían acumulándose en el tiempo sobre la pantalla creando un patrón con un único pico. Sin embargo, si ambas rendijas están abiertas los patrones de fotones incidiendo sobre la pantalla se convierten de nuevo en un patrón de líneas brillantes y oscuras. Este resultado parece confirmar y contradecir la teoría ondulatoria de la luz. Por un lado el patrón de interferencias confirma que la luz se comporta como una onda incluso si se envían partículas de una en una. Por otro lado, cada vez que un fotón de una cierta energía pasa por una de las rendijas el detector de la pantalla detecta la llegada de la misma cantidad de energía. Dado que los fotones se emiten uno a uno no pueden interferir globalmente así que no es fácil entender el origen de la "interferencia".

La teoría cuántica resuelve estos problemas postulando ondas de probabilidad que determinan la probabilidad de encontrar una partícula en un punto determinado, estas ondas de probabilidad interfieren entre sí como cualquier otra onda.

Un experimento más refinado consiste en disponer un detector en cada una de las dos rendijas para determinar por qué rendija pasa cada fotón antes de llegar a la pantalla. Sin embargo, cuando el experimento se dispone de esta manera las franjas desaparecen debido a la naturaleza indeterminista de la mecánica cuántica y al colapso de la función de onda.

Condiciones para la interferencia

Las ondas que producen interferencia han de ser "coherentes", es decir los haces provenientes de cada una de las rendijas han de mantener una fase relativa constante en el tiempo, además de mostrar la misma frecuencia; aunque esta última condición no es estrictamente necesaria, puesto que puede hacerse el experimento con luz blanca. Además, ambos han de tener polarizaciones no perpendiculares. En el experimento de Young esto se consigue al hacer pasar el haz por la primera rendija, produciendo una mutilación del frente de onda en dos frentes coherentes. También es posible observar franjas de interferencia con luz natural. En este caso se observa un máximo central blanco junto a otros máximos laterales de diferentes colores. Más allá, se observa un fondo blanco uniforme. Este fondo no está formado realmente por luz blanca, puesto que si, fijada una posición sobre la pantalla, se pone paralelo a la franja un espectrómetro por el cual se hace pasar la luz, se observan alternadamente franjas oscuras y brillantes. Esto se ha dado en llamar espectro acanalado. Las dos rendijas han de estar cerca (unas 1000 veces la longitud de onda de la luz utilizada) o en otro caso el patrón de interferencias solo se forma muy cerca de las rendijas. La anchura de las rendijas es normalmente algo más pequeña que la longitud de onda de la luz empleada permitiendo utilizar las ondas como fuentes puntuales esféricas y reduciendo los efectos de difracción por una única rendija.

Resultados observados

Se puede formular una relación entre las separaciones de las rendijas, $\Delta y$ , la longitud de onda $\lambda$ , la distancia de las rendijas a la pantalla $d$ , y la anchura de las bandas de interferencia (la distancia entre franjas brillantes sucesivas), $L$

\Delta y=L\lambda /d

Esta expresión es tan solo una aproximación y su formulación depende de ciertas condiciones específicas. Sin embargo, es posible calcular la longitud de onda de la luz incidente a partir de la relación superior. Si $\Delta y$ y $d$ son conocidos y $L$ es observado entonces $\lambda$ puede ser calculado, lo cual es de especial interés a la hora de medir la longitud de onda correspondiente a haces de electrones u otras partículas.

El espacio angular de las franjas, $θ f$ , viene dada por

\theta _{f}\approx \lambda /d

donde $θ f$ <<1, y $\lambda$ es la longitud de onda de la luz. Se puede observar que el espaciado de las franjas depende de la longitud de onda, de la separación de los agujeros y de la distancia entre las rendijas y el plano de observación, como señaló Young.

Véase también

Referencias

Young, Thomas (1 de enero de 1802). «II. The Bakerian Lecture. On the theory of light and colours». Philosophical Transactions of the Royal Society of London 92: 12-48. doi:10.1098/rstl.1802.0004. Consultado el 11 de agosto de 2022.
Young, Thomas (1804). The Bakerian lecture. El.1804.0001. S2CID 110408369. Consultado el 14 de julio de 2021.
Blog, The Physics arXiv (8 de noviembre de 2013). «Physicists Smash Record For Wave-Particle Duality». The Physics arXiv Blog (en inglés). Consultado el 3 de agosto de 2022.
Eibenberger, Sandra; Gerlich, Stefan; Arndt, Markus; Mayor, Marcel; Tüxen, Jens (2013). «Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu». Physical Chemistry Chemical Physics 15 (35): 14696. ISSN 1463-9076. doi:10.1039/C3CP51500A. Consultado el 3 de agosto de 2022.
Internet Archive, Andrew (2006). The last man who knew everything : Thomas Young, the anonymous polymath who proved Newton wrong, explained how we see, cured the sick, and deciphered the Rosetta stone, among other feats of genius. New York : Pi Press. ISBN 978-0-13-134304-7. Consultado el 3 de agosto de 2022.
Lederman, Leon M.; Christopher T. Hill (2011). Quantum Physics for Poets. US: Prometheus Books. pp. 102-111. ISBN 978-1616142810.
Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1965). The Feynman Lectures on Physics, Vol. 3. Addison-Wesley. pp. 1.1-1.8. ISBN 978-0201021189.
Feynman, 1965, p. 1.5
Darling, David (2007). «Wave–Particle Duality». The Internet Encyclopedia of Science. The Worlds of David Darling. Consultado el 18 de octubre de 2008.
Feynman, 1965, p. 1.7
Leon Lederman; Christopher T. Hill (27 de septiembre de 2011). Quantum Physics for Poets. Prometheus Books, Publishers. p. 109. ISBN 978-1-61614-281-0.
"...if in a double-slit experiment, the detectors which register outcoming photons are placed immediately behind the diaphragm with two slits: A photon is registered in one detector, not in both..." Müller-Kirsten, H. J. W. (2006). Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral. US: World Scientific. p. 14. ISBN 978-981-2566911.
Plotnitsky, Arkady (2012). Niels Bohr and Complementarity: An Introduction. US: Springer. pp. 75-76. ISBN 978-1461445173.
"It seems that light passes through one slit or the other in the form of photons if we set up an experiment to detect which slit the photon passes, but passes through both slits in the form of a wave if we perform an interference experiment." Rae, Alastair I.M. (2004). Quantum Physics: Illusion Or Reality?. UK: Cambridge University Press. pp. 9-10. ISBN 978-1139455275.
Feynman, The Feynman Lectures on Physics, 3:Quantum Mechanics p.1-1 "There is one lucky break, however— electrons behave just like light.".
See: Davisson–Germer experiment Davisson, C. J (1928). «The diffraction of electrons by a crystal of nickel». Bell System Technical Journal 7: 90-105. doi:10.1002/j.1538-7305.1928.tb00342.x.
Yaakov Y. Fein; Philipp Geyer; Patrick Zwick; Filip Kiałka; Sebastian Pedalino; Marcel Mayor; Stefan Gerlich; Markus Arndt (September 2019). «Quantum superposition of molecules beyond 25 kDa». Nature Physics 15 (12): 1242-1245. Bibcode:2019NatPh..15.1242F. S2CID 203638258. doi:10.1038/s41567-019-0663-9.
Greene, Brian (2007). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. Random House LLC. p. 90. ISBN 978-0-307-42853-0.
Donati, O; Missiroli, G F; Pozzi, G (1973). «An Experiment on Electron Interference». American Journal of Physics 41 (5): 639-644. Bibcode:1973AmJPh..41..639D. doi:10.1119/1.1987321.
«Wave Particle Duality of C60». Archivado desde el original el 31 de marzo de 2012. Consultado el 3 de agosto de 2022.
lNairz, Olaf; Brezger, Björn; Arndt, Markus; Anton Zeilinger, Abstract (2001). «Diffraction of Complex Molecules by Structures Made of Light». Phys. Rev. Lett. 87 (16): 160401. Bibcode:2001PhRvL..87p0401N. PMID 11690188. S2CID 21547361. arXiv:quant-ph/0110012. doi:10.1103/physrevlett.87.160401.
Nairz, O; Arndt, M; Zeilinger, A (2003). «Quantum interference experiments with large molecules». American Journal of Physics 71 (4): 319-325. Bibcode:2003AmJPh..71..319N. doi:10.1119/1.1531580. Archivado desde el original el 8 de agosto de 2017. Consultado el 4 de junio de 2015.
Stefan Gerlich (Apr 5, 2011). «Quantum interference of large organic molecules». Nature Communications 2: 263. Bibcode:2011NatCo...2..263G. PMC 3104521. PMID 21468015. doi:10.1038/ncomms1263.
Yaakov Fein (Dec 2019). «Quantum superposition of molecules beyond 25kDa». Nature Physics 15 (12): 1242-1245. Bibcode:2019NatPh..15.1242F. S2CID 203638258. doi:10.1038/s41567-019-0663-9.
Greene, Brian (2004). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. Knopf. pp. 204–213. ISBN 978-0-375-41288-2.
Sala, S.; Ariga, A.; Ereditato, A.; Ferragut, R.; Giammarchi, M.; Leone, M.; Pistillo, C.; Scampoli, P. (3 de mayo de 2019). «First demonstration of antimatter wave interferometry». Science Advances (en inglés) 5 (5): eaav7610. ISSN 2375-2548. PMID 31058223. doi:10.1126/sciadv.aav7610. Consultado el 21 de diciembre de 2022.
Vedral, Vlatko (2006). Introduction to Quantum Information Science. Oxford University Press. ISBN 9780199215706. OCLC 442351498.
Harrison, David (2002). «Complementarity and the Copenhagen Interpretation of Quantum Mechanics». UPSCALE. Dept. of Physics, U. of Toronto. Consultado el 21 de junio de 2008.
Cassidy, David (2008). «Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation». Werner Heisenberg. American Institute of Physics. Archivado desde el original el 14 de enero de 2016. Consultado el 3 de agosto de 2022.
Boscá Díaz-Pintado, María C. (29–31 March 2007). «Updating the wave–particle duality». 15th UK and European Meeting on the Foundations of Physics. Leeds, UK. Consultado el 21 de junio de 2008.
Bartell, L. (1980). «Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior». Physical Review D 21 (6): 1698-1699. Bibcode:1980PhRvD..21.1698B. doi:10.1103/PhysRevD.21.1698.
Zeilinger, A. (1999). «Experiment and the foundations of quantum physics». Reviews of Modern Physics 71 (2): S288-S297. Bibcode:1999RvMPS..71..288Z. doi:10.1103/RevModPhys.71.S288.
P. Mittelstaedt; A. Prieur; R. Schieder (1987). «Unsharp particle-wave duality in a photon split-beam experiment». Foundations of Physics 17 (9): 891-903. Bibcode:1987FoPh...17..891M. S2CID 122856271. doi:10.1007/BF00734319.
D.M. Greenberger y A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer", Physics Letters A 128, 391-4 (1988).
Wootters, W. K.; Zurek, W. H. (1979). «Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr's principle». Phys. Rev. D 19 (2): 473-484. Bibcode:1979PhRvD..19..473W. doi:10.1103/PhysRevD.19.473. Archivado desde el original el 22 de febrero de 2014. Consultado el 5 de febrero de 2014.
Hillmer, R.; Kwiat, P. (2007). «A do-it-yourself quantum eraser». Scientific American 296 (5): 90-95. Bibcode:2007SciAm.296e..90H. doi:10.1038/scientificamerican0507-90. Consultado el 11 de enero de 2016.
Chiao, R. Y.; P. G. Kwiat; Steinberg, A. M. (1995). «Quantum non-locality in two-photon experiments at Berkeley». Quantum and Semiclassical Optics: Journal of the European Optical Society Part B 7 (3): 259-278. Bibcode:1995QuSOp...7..259C. S2CID 118987962. arXiv:quant-ph/9501016. doi:10.1088/1355-5111/7/3/006.
Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York
Longhurst RS, Physical and Geometrical Optics, 1967, 2nd Edition, Longmans
Rovelli, Carlo (1996). «Relational Quantum Mechanics». International Journal of Theoretical Physics 35 (8): 1637-1678. Bibcode:1996IJTP...35.1637R. S2CID 16325959. arXiv:quant-ph/9609002. doi:10.1007/BF02302261.
Philippidis, C.; Dewdney, C.; Hiley, B. J. (1979). «Quantum interference and the quantum potential». Il Nuovo Cimento B (en inglés) 52 (1): 15-28. Bibcode:1979NCimB..52...15P. ISSN 1826-9877. S2CID 53575967. doi:10.1007/bf02743566.
«Bohmian Mechanics». The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 2017.
Richard P. Feynman, Robert B. Leighton, and Matthew Sands (1965). «1». The Feynman Lectures on Physics Vol III (en inglés). Addison–Wesley. Archivado desde el original el 26 de noviembre de 2018. Consultado el 13 de julio de 2018.

Bibliografía

Richard P. Feynman, Robert B. Leighton y Matthew Sands, The Feynman Lectures on Physics, Vol III, Capítulo 1. Addison Wesley (español).
Thomas Young, Experimental Demonstration of the General Law of the Interference of Light, "Philosophical Transactions of the Royal Society of London", vol 94, 2 (1804). El artículo puede encontrarse en Morris Shamos, ed., "Great Experiments in Physics" p96-101, Holt Reinhart and Winston, New York, 1959.
https://es.quora.com/Por-qu%C3%A9-casi-nadie-entiende-la-f%C3%ADsica-cu%C3%A1ntica/answer/Enrique-Casanovas-3

Enlaces externos

Formulación clásica del experimento (en inglés)
Physics World (en inglés)
Versión del experimento de Young-Feynman (en inglés)
https://es.quora.com/Por-qu%C3%A9-casi-nadie-entiende-la-f%C3%ADsica-cu%C3%A1ntica/answer/Enrique-Casanovas-3
Laboratorio Positrones (L-NESS)

Datos: Q217785
Multimedia: Double-slit experiments / Q217785

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Young, Thomas (1 de enero de 1802). «II. The Bakerian Lecture. On the theory of light and colours». Philosophical Transactions of the Royal Society of London 92: 12-48. doi:10.1098/rstl.1802.0004. Consultado el 11 de agosto de 2022.

[The_Bakerian_lecture-2] Young, Thomas (1804). The Bakerian lecture. El.1804.0001. S2CID 110408369. Consultado el 14 de julio de 2021.

[3] Blog, The Physics arXiv (8 de noviembre de 2013). «Physicists Smash Record For Wave-Particle Duality». The Physics arXiv Blog (en inglés). Consultado el 3 de agosto de 2022.

[4] Eibenberger, Sandra; Gerlich, Stefan; Arndt, Markus; Mayor, Marcel; Tüxen, Jens (2013). «Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu». Physical Chemistry Chemical Physics 15 (35): 14696. ISSN 1463-9076. doi:10.1039/C3CP51500A. Consultado el 3 de agosto de 2022.

[5] Internet Archive, Andrew (2006). The last man who knew everything : Thomas Young, the anonymous polymath who proved Newton wrong, explained how we see, cured the sick, and deciphered the Rosetta stone, among other feats of genius. New York : Pi Press. ISBN 978-0-13-134304-7. Consultado el 3 de agosto de 2022.

[Lederman-6] Lederman, Leon M.; Christopher T. Hill (2011). Quantum Physics for Poets. US: Prometheus Books. pp. 102-111. ISBN 978-1616142810.

[Feynman-7] Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1965). The Feynman Lectures on Physics, Vol. 3. Addison-Wesley. pp. 1.1-1.8. ISBN 978-0201021189.

[8] Feynman, 1965, p. 1.5

[9] Darling, David (2007). «Wave–Particle Duality». The Internet Encyclopedia of Science. The Worlds of David Darling. Consultado el 18 de octubre de 2008.

[10] Feynman, 1965, p. 1.7

[11] Leon Lederman; Christopher T. Hill (27 de septiembre de 2011). Quantum Physics for Poets. Prometheus Books, Publishers. p. 109. ISBN 978-1-61614-281-0.

[Müller-Kirsten-12] "...if in a double-slit experiment, the detectors which register outcoming photons are placed immediately behind the diaphragm with two slits: A photon is registered in one detector, not in both..." Müller-Kirsten, H. J. W. (2006). Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral. US: World Scientific. p. 14. ISBN 978-981-2566911.

[Plotnitsky-13] Plotnitsky, Arkady (2012). Niels Bohr and Complementarity: An Introduction. US: Springer. pp. 75-76. ISBN 978-1461445173.

[Rae-14] "It seems that light passes through one slit or the other in the form of photons if we set up an experiment to detect which slit the photon passes, but passes through both slits in the form of a wave if we perform an interference experiment." Rae, Alastair I.M. (2004). Quantum Physics: Illusion Or Reality?. UK: Cambridge University Press. pp. 9-10. ISBN 978-1139455275.

[15] Feynman, The Feynman Lectures on Physics, 3:Quantum Mechanics p.1-1 "There is one lucky break, however— electrons behave just like light.".

[16] See: Davisson–Germer experiment Davisson, C. J (1928). «The diffraction of electrons by a crystal of nickel». Bell System Technical Journal 7: 90-105. doi:10.1002/j.1538-7305.1928.tb00342.x.

[17] Yaakov Y. Fein; Philipp Geyer; Patrick Zwick; Filip Kiałka; Sebastian Pedalino; Marcel Mayor; Stefan Gerlich; Markus Arndt (September 2019). «Quantum superposition of molecules beyond 25 kDa». Nature Physics 15 (12): 1242-1245. Bibcode:2019NatPh..15.1242F. S2CID 203638258. doi:10.1038/s41567-019-0663-9.

[18] Greene, Brian (2007). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. Random House LLC. p. 90. ISBN 978-0-307-42853-0.

[19] Donati, O; Missiroli, G F; Pozzi, G (1973). «An Experiment on Electron Interference». American Journal of Physics 41 (5): 639-644. Bibcode:1973AmJPh..41..639D. doi:10.1119/1.1987321.

[20] «Wave Particle Duality of C60». Archivado desde el original el 31 de marzo de 2012. Consultado el 3 de agosto de 2022.

[21] Nairz, Olaf; Brezger, Björn; Arndt, Markus; Anton Zeilinger, Abstract (2001). «Diffraction of Complex Molecules by Structures Made of Light». Phys. Rev. Lett. 87 (16): 160401. Bibcode:2001PhRvL..87p0401N. PMID 11690188. S2CID 21547361. arXiv:quant-ph/0110012. doi:10.1103/physrevlett.87.160401.

[22] Nairz, O; Arndt, M; Zeilinger, A (2003). «Quantum interference experiments with large molecules». American Journal of Physics 71 (4): 319-325. Bibcode:2003AmJPh..71..319N. doi:10.1119/1.1531580. Archivado desde el original el 8 de agosto de 2017. Consultado el 4 de junio de 2015.

[23] Stefan Gerlich (Apr 5, 2011). «Quantum interference of large organic molecules». Nature Communications 2: 263. Bibcode:2011NatCo...2..263G. PMC 3104521. PMID 21468015. doi:10.1038/ncomms1263.

[24] Yaakov Fein (Dec 2019). «Quantum superposition of molecules beyond 25kDa». Nature Physics 15 (12): 1242-1245. Bibcode:2019NatPh..15.1242F. S2CID 203638258. doi:10.1038/s41567-019-0663-9.

[Greene_2004-25] Greene, Brian (2004). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. Knopf. pp. 204–213. ISBN 978-0-375-41288-2.

[26] Sala, S.; Ariga, A.; Ereditato, A.; Ferragut, R.; Giammarchi, M.; Leone, M.; Pistillo, C.; Scampoli, P. (3 de mayo de 2019). «First demonstration of antimatter wave interferometry». Science Advances (en inglés) 5 (5): eaav7610. ISSN 2375-2548. PMID 31058223. doi:10.1126/sciadv.aav7610. Consultado el 21 de diciembre de 2022.

[vedral-27] Vedral, Vlatko (2006). Introduction to Quantum Information Science. Oxford University Press. ISBN 9780199215706. OCLC 442351498.

[28] Harrison, David (2002). «Complementarity and the Copenhagen Interpretation of Quantum Mechanics». UPSCALE. Dept. of Physics, U. of Toronto. Consultado el 21 de junio de 2008.

[29] Cassidy, David (2008). «Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation». Werner Heisenberg. American Institute of Physics. Archivado desde el original el 14 de enero de 2016. Consultado el 3 de agosto de 2022.

[30] Boscá Díaz-Pintado, María C. (29–31 March 2007). «Updating the wave–particle duality». 15th UK and European Meeting on the Foundations of Physics. Leeds, UK. Consultado el 21 de junio de 2008.

[Bartell1980-31] Bartell, L. (1980). «Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior». Physical Review D 21 (6): 1698-1699. Bibcode:1980PhRvD..21.1698B. doi:10.1103/PhysRevD.21.1698.

[Zeilinger1999-32] Zeilinger, A. (1999). «Experiment and the foundations of quantum physics». Reviews of Modern Physics 71 (2): S288-S297. Bibcode:1999RvMPS..71..288Z. doi:10.1103/RevModPhys.71.S288.

[Mittelstaedt-33] P. Mittelstaedt; A. Prieur; R. Schieder (1987). «Unsharp particle-wave duality in a photon split-beam experiment». Foundations of Physics 17 (9): 891-903. Bibcode:1987FoPh...17..891M. S2CID 122856271. doi:10.1007/BF00734319.

[34] D.M. Greenberger y A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer", Physics Letters A 128, 391-4 (1988).

[WoottersZurek1979-35] Wootters, W. K.; Zurek, W. H. (1979). «Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr's principle». Phys. Rev. D 19 (2): 473-484. Bibcode:1979PhRvD..19..473W. doi:10.1103/PhysRevD.19.473. Archivado desde el original el 22 de febrero de 2014. Consultado el 5 de febrero de 2014.

[Hillmer2007-36] Hillmer, R.; Kwiat, P. (2007). «A do-it-yourself quantum eraser». Scientific American 296 (5): 90-95. Bibcode:2007SciAm.296e..90H. doi:10.1038/scientificamerican0507-90. Consultado el 11 de enero de 2016.

[Chiao1995-37] Chiao, R. Y.; P. G. Kwiat; Steinberg, A. M. (1995). «Quantum non-locality in two-photon experiments at Berkeley». Quantum and Semiclassical Optics: Journal of the European Optical Society Part B 7 (3): 259-278. Bibcode:1995QuSOp...7..259C. S2CID 118987962. arXiv:quant-ph/9501016. doi:10.1088/1355-5111/7/3/006.

[38] Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York

[39] Longhurst RS, Physical and Geometrical Optics, 1967, 2nd Edition, Longmans

[40] Rovelli, Carlo (1996). «Relational Quantum Mechanics». International Journal of Theoretical Physics 35 (8): 1637-1678. Bibcode:1996IJTP...35.1637R. S2CID 16325959. arXiv:quant-ph/9609002. doi:10.1007/BF02302261.

[41] Philippidis, C.; Dewdney, C.; Hiley, B. J. (1979). «Quantum interference and the quantum potential». Il Nuovo Cimento B (en inglés) 52 (1): 15-28. Bibcode:1979NCimB..52...15P. ISSN 1826-9877. S2CID 53575967. doi:10.1007/bf02743566.

[42] «Bohmian Mechanics». The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 2017.

[43] Richard P. Feynman, Robert B. Leighton, and Matthew Sands (1965). «1». The Feynman Lectures on Physics Vol III (en inglés). Addison–Wesley. Archivado desde el original el 26 de noviembre de 2018. Consultado el 13 de julio de 2018.