Facetado
En geometría, el facetado es el proceso de eliminar partes de un polígono, poliedro o politopo, sin crear ningún vértice nuevo.

Se pueden crear nuevas aristas de un poliedro facetado a lo largo de las diagonales faciales o las diagonales espaciales internas. Un poliedro facetado tendrá dos caras por cada arista del poliedro original, generando nuevos poliedros o compuestos de poliedros.
El facetado es el proceso recíproco o dual de la estelación. Para cada estelación de un politopo convexo, existe el correspondiente facetado del politopo dual.
Polígonos facetados
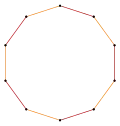
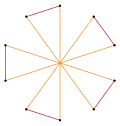
Por ejemplo, un pentágono regular posee un facetado simétrico, el pentagrama; y el hexágono regular posee dos facetados simétricos, uno como un polígono y otro como el compuesto de dos triángulos.
| Pentágono | Hexágono | Decágono | |||||||
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 | |||||||
| Pentagrama {5/2} |
Hexágono estrellado |
Compuesto 2 {3} |
Decagrama {10/3} |
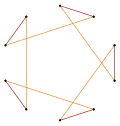
Compuesto 2 {5} |
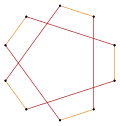
Compuesto 2 {5/2} |
Decágono estrellado | |||
 |
 |
.svg.png.webp) |
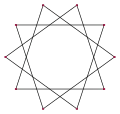 |
.svg.png.webp) |
.svg.png.webp) |
 |
 |
 |
 |
Poliedros facetados
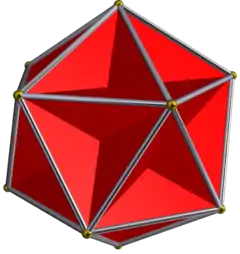
El icosaedro regular se puede facetar en tres poliedros de Kepler-Poinsot regulares: el pequeño dodecaedro estrellado, el gran dodecaedro y el gran icosaedro. Todos tienen 30 aristas.
| Convexo | Estrellas regulares | ||
|---|---|---|---|
| Icosaedro | Gran dodecaedro | Pequeño dodecaedro estrellado | Gran icosaedro |
 |
 |
 |
 |
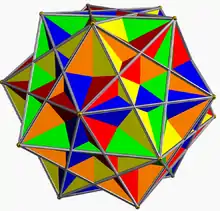
El dodecaedro regular puede ser facetado en un poliedro de Kepler-Poinsot regular, tres poliedros estrellados uniformes y tres compuestos poliédricos regulares. Las formas estrelladas uniformes y el compuesto de cinco cubos están construidos por diagonales faciales. El dodecaedro excavado es un facetado con caras hexagonales en forma de estrella.
| Convexo | Estrella regular | Estrellas uniformes | Vértice transitivo | ||
|---|---|---|---|---|---|
| Dodecaedro | Gran dodecaedro estrellado | Pequeño icosi-dodecaedro ditrigonal | Dodeca-dodecaedro ditrigonal | Gran icosi-dodecaedro ditrigonal | Dodecaedro excavado |
 |
 |
 |
 |
 |
 |
| Convexo | Compuestos regulares | ||
|---|---|---|---|
| Dodecaedro | Cinco tetraedros | Cinco cubos | Diez tetraedros |
 |
 |
 |
 |
Historia
El facetado no se ha estudiado tan ampliamente como la estelación.
- En 1568 Wenzel Jamnitzer publicó su libro Perspectiva Corporum Regularium, que muestra muchas estelaciones y facetados de poliedros.[1]
- En 1619, Kepler describió un compuesto regular de dos tetraedros que cabe dentro de un cubo, y que llamó la Stella octangula.
- En 1858, Bertrand derivó el poliedro estrellado regular (poliedro de Kepler-Poinsot) al enfrentar el icosaedro convexo regular y el dodecaedro.
- En 1974, Bridge enumeró las facetados más directos de los poliedros regulares, incluidos los del dodecaedro.
- En 2006, Inchbald describió la teoría básica de los diagramas de facetado para poliedros. Para un vértice dado, el diagrama muestra todos los bordes y facetas posibles (caras nuevas) que se pueden usar para formar facetas del poliedro original. Es dual al diagrama de stelación de los poliedros duales, que muestra todos los bordes y vértices posibles para alguna cara plana del núcleo original.
Referencias
- Mathematical Treasure: Wenzel Jamnitzer's Platonic Solids by Frank J. Swetz (2013): "In this study of the five Platonic solids, Jamnitzer truncated, stellated, and faceted the regular solids [...]"
Bibliografía
- Bertrand, J. Note sur the théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46 (1858), pp. 79-82.
- Bridge, NJ Facetar el dodecaedro, Acta crystallographica A30 (1974), pp. 548–552.
- Inchbald, G. Diagramas de facetas, The Gaceta matemática, 90 (2006), pp. 253–261.
- Alan Holden, Formas, espacio y simetría . Nueva York: Dover, 1991. p.94
Enlaces externos
- Weisstein, Eric W. «Faceting». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Olshevsky, George. "Faceting". Glossary for Hyperspace. Original archivado el 4 de febrero de 2007.

