Compuesto de cinco cubos
El compuesto de cinco cubos es un poliedro compuesto regular. Fue descrito por primera vez por Edmund Hess en 1876, y es uno de los cinco compuestos regulares, dual del compuesto de cinco octaedros.
| Compuesto de cinco cubos | |
|---|---|
 (Animación, Modelo 3D) | |
| Tipo | Compuesto regular |
| Símbolo de Coxeter | 2{5,3}[5{4,3}][1] |
| Núcleo de la estelación | Triacontaedro rómbico |
| Envolvente convexa | Dodecaedro |
| Índice | UC9 |
| Poliedros | 5 cubos |
| Caras | 30 cuadrados (o también 360 triángulos exteriores) |
| Aristas | 60 |
| Vértices | 20 |
| Dual | Compuesto de cinco octaedros |
| Grupo de simetría | Icosaédrico (Ih) |
| Subgrupo restringido a un elemento | Piritoedral (Th) |


Posee simetría icosaédrica (Ih), y puede verse como el facetado de un dodecaedro regular, y también como una de las estelaciones del triacontaedro rómbico.
Geometría
El compuesto es un facetado de un dodecaedro (donde se pueden ver pentagramas en correlación con las caras pentagonales). Cada cubo representa una selección de 8 de los 20 vértices del dodecaedro.
 |
 |
 |
 |
| Vista de los ejes de simetría de 2, 5 y 3 lóbulos | |||
Si la forma se considera como una unión de cinco cubos que producen un sólido simple no convexo sin superficies autointersecantes, entonces tiene 360 caras (todas triángulos), 182 vértices (60 de grado 3, 30 de grado 4, 12 de grado 5, 60 con grado 8 y 20 con grado 12) y 540 aristas, con una característica de Euler de 182 − 540 + 360 = 2.
Disposición de aristas
Su envolvente convexa es un dodecaedro regular. Además, comparte su disposición de vértices con el pequeño icosidodecaedro ditrigonal, el gran icosidodecaedro ditrigonal y el dodecadodecaedro ditrigonal. Con estas figuras, es posible formar compuestos poliédricos que también pueden ser considerados como poliedros estrellados uniformes degenerados: el pequeño rombicosidodecaedro complejo, el gran rombicosidodecaedro complejo y el rombicosidodecaedro complejo.
 Pequeño icosidodecaedro ditrigonal |
 Gran icosidodecaedro ditrigonal |
 Dodecadodecaedro ditrigonal |
 Dodecaedro (envolvente convexa) |
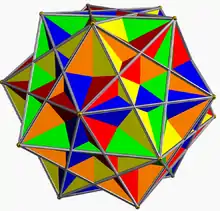 Compuesto de cinco cubos |
 Como un poliedro esférico |
El compuesto de diez tetraedros se puede formar tomando cada uno de estos cinco cubos y reemplazándolos por los dos tetraedros de la estrella octángula (que comparten la misma disposición de vértices de un cubo).
Como una estelación
 Facetas de estelación El área amarilla corresponde a una cara del cubo |
Este compuesto puede formarse como una estelación del triacontaedro rómbico. |
Véase también
Referencias
- Regular polytopes, pp.49-50, p.98
Bibliografía
- Cromwell, Peter R. (1997), Polyhedra, Cambridge.. pág. 360
- Harman, Michael G. (c. 1974), Polyhedral Compounds, unpublished manuscript..
- Skilling, John (1976), «Uniform Compounds of Uniform Polyhedra», Mathematical Proceedings of the Cambridge Philosophical Society 79: 447-457, MR 0397554, doi:10.1017/S0305004100052440..
- Cundy, H. y Rollett, A. "Cinco cubos en un dodecaedro". §3.10.6 en Mathematical Models, 3ra ed. Stradbroke, Inglaterra: Tarquin Pub., pp. 135–136, 1989.
- H.S.M. Coxeter, Regular Polytopes, (3ra edición, 1973), edición de Dover, ISBN 0-486-61480-8, 3.6 Los cinco compuestos regulares, pp.47-50, 6.2 Estrellando los sólidos platónicos, pp.96 -104
Enlaces externos
- MathWorld: Cubo 5-Compuesto
- George Hart: Compuestos de cubos
- Steven Dutch: poliedros uniformes y sus duales
- Modelo VRML: (Enlace roto: julio de 2020)
- Klitzing, Richard. «3D compound».