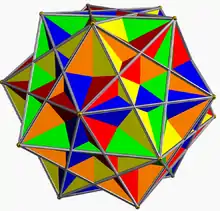
Gran icosidodecaedro ditrigonal

En geometría, el gran icosidodecaedro ditrigonal (o gran icosidodecaedro ditrigonario) es un poliedro uniforme estrellado, indexado como U₄₇. Tiene 32 caras (20 triángulos y 12 pentágonos), 60 aristas y 20 vértices.[1] Tiene 4 construcciones equivalentes al triángulo de Schwarz; por ejemplo, con símbolo de Wythoff 3 | 3 ⁵⁄₄ se genera el diagrama de Coxeter-Dynkin = . Se representa mediante el símbolo de Schläfli extendido a{⁵⁄₂,3} o c{3,⁵⁄₂}, como un gran dodecaedro estrellado alterado o un gran icosaedro convertido.

Gran icosidodecaedro ditrigonal
Modelo 3D
Tipo	poliedro uniforme, poliedro no convexo y poliedro ditrigonal
Forma de las caras	triángulo equilátero (20) pentágono regular (12)
Configuración de vértices	hexágono
Símbolo de Schläfli	a{5/2,3} y c{3,5/2}
Dual	great triambic icosahedron (en)
Elementos
Vértices	20
Aristas	60
Caras	32

Su circunradio es la ${\textstyle {\frac {\sqrt {3}}{2}}}$ parte de su arista,[2] un valor que comparte con el cubo.