Compuesto poliédrico uniforme
Un compuesto poliédrico uniforme es un compuesto poliédrico cuyos componentes son poliedros uniformes idénticos (aunque también se considera que puedan ser enantiomorfos), en una disposición que también es uniforme; es decir, el grupo de simetría del compuesto actúa transitivamente sobre los vértices del compuesto.
Los compuestos poliédricos uniformes fueron enumerados por primera vez por John Skilling en 1976, con una prueba de que la enumeración estaba completa. La siguiente tabla los enumera según la numeración de Skilling.
Los compuestos prismáticos de prismas p/q-gonales UC20 y UC21 solo existen cuando pq > 2, y cuando p y q son coprimos. Los compuestos prismáticos de antiprismas p/q-gonales UC22, UC23, UC24 y UC25 solo existen cuando pq > 32 y cuando p y q son coprimos. Además, cuando pq = 2, los antiprismas se degeneran en tetraedros con bases digonales.
| Compuesto | Acrónimo de Bowers | Imagen | Cuenta poliédrica | Tipo de poliedro | Caras | Aristas | Vértices | Notas | Grupo de simetría | Subgrupo restringido a un componente |
|---|---|---|---|---|---|---|---|---|---|---|
| UC01 | sis |  |
6 | Tetraedros | 24{3} | 36 | 24 | Libertad rotacional | Td | S4 |
| UC02 | dis | 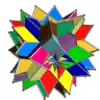 |
12 | Tetraedros | 48{3} | 72 | 48 | Libertad rotacional | Oh | S4 |
| UC03 | snu | 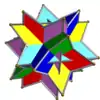 |
6 | Tetraedros | 24{3} | 36 | 24 | Oh | D2d | |
| UC04 | so |  |
2 | Tetraedros | 8{3} | 12 | 8 | Regular | Oh | Td |
| UC05 | ki |  |
5 | Tetraedros | 20{3} | 30 | 20 | Regular | I | T |
| UC06 | e |  |
10 | Tetraedros | 40{3} | 60 | 20 | Regular
2 poliedros por vértice |
Ih | T |
| UC07 | risdoh | 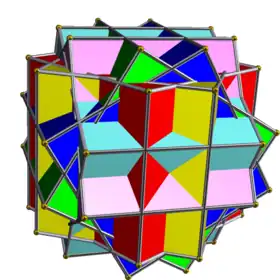 |
6 | Cubos | (12+24){4} | 72 | 48 | Libertad rotacional | Oh | C4h |
| UC08 | rah | 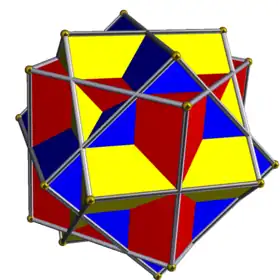 |
3 | Cubos | (6+12){4} | 36 | 24 | Oh | D4h | |
| UC09 | rhom |  |
5 | Cubos | 30{4} | 60 | 20 | Regular
2 poliedros por vértice |
Ih | Th |
| UC10 | dissit | 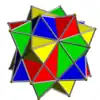 |
4 | Octaedros | (8+24){3} | 48 | 24 | Libertad rotacional | Th | S6 |
| UC11 | daso | 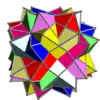 |
8 | Octaedros | (16+48){3} | 96 | 48 | Libertad rotacional | Oh | S6 |
| UC12 | sno | 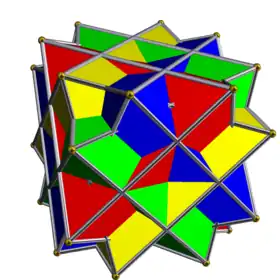 |
4 | Octaedros | (8+24){3} | 48 | 24 | Oh | D3d | |
| UC13 | addasi |  |
20 | Octaedros | (40+120){3} | 240 | 120 | Libertad rotacional | Ih | S6 |
| UC14 | dasi |  |
20 | Octaedros | (40+120){3} | 240 | 60 | 2 poliedros por vértice | Ih | S6 |
| UC15 | gissi | 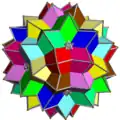 |
10 | Octaedros | (20+60){3} | 120 | 60 | Ih | D3d | |
| UC16 | si | 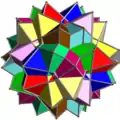 |
10 | Octaedros | (20+60){3} | 120 | 60 | Ih | D3d | |
| UC17 | se | 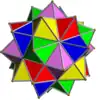 |
5 | Octaedros | 40{3} | 60 | 30 | Regular | Ih | Th |
| UC18 | hirki |  |
5 | Tetrahemihexaedros | 20{3}
15{4} |
60 | 30 | I | T | |
| UC19 | sapisseri |  |
20 | Tetrahemihexaedros | (20+60){3}
60{4} |
240 | 60 | 2 poliedros por vértice | I | C3 |
| UC20 | - | 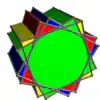 |
2n
(2n ≥ 2) |
Prismas p/q-gonales | 4n{p/q}
2np{4} |
6np | 4np | Libertad rotacional | Dnph | Cph |
| UC21 | - |  |
n
(n ≥ 2) |
Prismas p/q-gonales | 2n{p/q}
np{4} |
3np | 2np | Dnph | Dph | |
| UC22 | - | 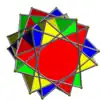 |
2n
(2n ≥ 2) (q impar) |
Antiprismas p/q-gonales
(q impar) |
4n{p/q} (si pq ≠ 2)
4np{3} |
8np | 4np | Libertad rotacional | Dnpd (si n es impar)
Dnph (si n es par) |
S2p |
| UC23 | - | 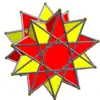 |
n
(n ≥ 2) |
Antiprismas p/q-gonales
(q odd) |
2n{p/q} (si pq ≠ 2)
2np{3} |
4np | 2np | Dnpd (si n es impar)
Dnph (si n es par) |
Dpd | |
| UC24 | - | 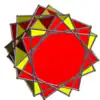 |
2n
(2n ≥ 2) |
Antiprismas p/q-gonales
(q par) |
4n{p/q} (si pq ≠ 2)
4np{3} |
8np | 4np | Libertad rotacional | Dnph | Cph |
| UC25 | - | 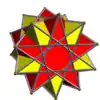 |
n
(n ≥ 2) |
Antiprismas p/q-gonales
(q par) |
2n{p/q} (si pq ≠ 2)
2np{3} |
4np | 2np | Dnph | Dph | |
| UC26 | gadsid |  |
12 | Antiprismas pentagonales | 120{3}
24{5} |
240 | 120 | Libertad rotacional | Ih | S10 |
| UC27 | gassid |  |
6 | Antiprismas pentagonales | 60{3}
12{5} |
120 | 60 | Ih | D5d | |
| UC28 | gidasid |  |
12 | Antiprismas pentagonales cruzados | 120{3}
24{5/2} |
240 | 120 | Libertad rotacional | Ih | S10 |
| UC29 | gissed |  |
6 | Antiprismas pentagonales cruzados | 60{3}
12{5/2} |
120 | 60 | Ih | D5d | |
| UC30 | ro |  |
4 | Prismas triangulares | 8{3}
12{4} |
36 | 24 | O | D3 | |
| UC31 | dro |  |
8 | Prismas triangulares | 16{3}
24{4} |
72 | 48 | Oh | D3 | |
| UC32 | kri | 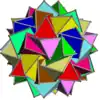 |
10 | Prismas triangulares | 20{3}
30{4} |
90 | 60 | I | D3 | |
| UC33 | dri |  |
20 | Prismas triangulares | 40{3}
60{4} |
180 | 60 | 2 poliedros por vértice | Ih | D3 |
| UC34 | kred |  |
6 | Prismas pentagonales | 30{4}
12{5} |
90 | 60 | I | D5 | |
| UC35 | dird |  |
12 | Prismas pentagonales | 60{4}
24{5} |
180 | 60 | 2 poliedros por vértice | Ih | D5 |
| UC36 | gikrid |  |
6 | Prismas pentagrámicos | 30{4}
12{5/2} |
90 | 60 | I | D5 | |
| UC37 | giddird |  |
12 | Prismas pentagrámicos | 60{4}
24{5/2} |
180 | 60 | 2 poliedros por vértice | Ih | D5 |
| UC38 | griso |  |
4 | Prismas hexagonales | 24{4}
8{6} |
72 | 48 | Oh | D3d | |
| UC39 | rosi |  |
10 | Prismas hexagonales | 60{4}
20{6} |
180 | 120 | Ih | D3d | |
| UC40 | rassid |  |
6 | Prismas decagonales | 60{4}
12{10} |
180 | 120 | Ih | D5d | |
| UC41 | grassid | 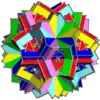 |
6 | Prismas decagrámicos | 60{4}
12{10/3} |
180 | 120 | Ih | D5d | |
| UC42 | gassic | 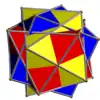 |
3 | Antiprismas cuadrados | 24{3}
6{4} |
48 | 24 | O | D4 | |
| UC43 | gidsac | 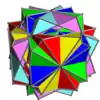 |
6 | Antiprismas cuadrados | 48{3}
12{4} |
96 | 48 | Oh | D4 | |
| UC44 | sassid |  |
6 | Antiprismas pentagrámicos | 60{3}
12{5/2} |
120 | 60 | I | D5 | |
| UC45 | sadsid |  |
12 | Antiprismas pentagrámicos | 120{3}
24{5/2} |
240 | 120 | Ih | D5 | |
| UC46 | siddo |  |
2 | Icosaedros | (16+24){3} | 60 | 24 | Oh | Th | |
| UC47 | sne | 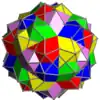 |
5 | Icosaedros | (40+60){3} | 150 | 60 | Ih | Th | |
| UC48 | presipsido |  |
2 | Grandes dodecaedros | 24{5} | 60 | 24 | Oh | Th | |
| UC49 | presipsi | 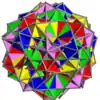 |
5 | Grandes dodecaedros | 60{5} | 150 | 60 | Ih | Th | |
| UC50 | passipsido |  |
2 | Pequeños dodecaedros estellados | 24{5/2} | 60 | 24 | Oh | Th | |
| UC51 | passipsi |  |
5 | Pequeños dodecaedros estellados | 60{5/2} | 150 | 60 | Ih | Th | |
| UC52 | sirsido |  |
2 | Grandes icosaedros | (16+24){3} | 60 | 24 | Oh | Th | |
| UC53 | sirsei |  |
5 | Grandes icosaedros | (40+60){3} | 150 | 60 | Ih | Th | |
| UC54 | tisso |  |
2 | Tetraedros truncados | 8{3}
8{6} |
36 | 24 | Oh | Td | |
| UC55 | taki |  |
5 | Tetraedros truncados | 20{3}
20{6} |
90 | 60 | I | T | |
| UC56 | te |  |
10 | Tetraedros truncados | 40{3}
40{6} |
180 | 120 | Ih | T | |
| UC57 | tar | 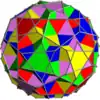 |
5 | Cubos truncados | 40{3}
30{8} |
180 | 120 | Ih | Th | |
| UC58 | quitar | 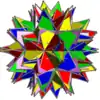 |
5 | Hexaedros truncados estrellados | 40{3}
30{8/3} |
180 | 120 | Ih | Th | |
| UC59 | arie |  |
5 | Cuboctaedros | 40{3}
30{4} |
120 | 60 | Ih | Th | |
| UC60 | gari |  |
5 | Cubohemioctaedros | 30{4}
20{6} |
120 | 60 | Ih | Th | |
| UC61 | iddei | 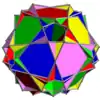 |
5 | Octahemioctaedros | 40{3}
20{6} |
120 | 60 | Ih | Th | |
| UC62 | rasseri |  |
5 | Rombicuboctaedros | 40{3}
(30+60){4} |
240 | 120 | Ih | Th | |
| UC63 | rasher |  |
5 | Pequeño rombihexaedro | 60{4}
30{8} |
240 | 120 | Ih | Th | |
| UC64 | rahrie |  |
5 | Pequeños cubicuboctaedros | 40{3}
30{4} 30{8} |
240 | 120 | Ih | Th | |
| UC65 | raquahri | 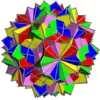 |
5 | Gran cubicuboctaedros | 40{3}
30{4} 30{8/3} |
240 | 120 | Ih | Th | |
| UC66 | rasquahr |  |
5 | Grandes rombihexaedros | 60{4}
30{8/3} |
240 | 120 | Ih | Th | |
| UC67 | rosaqri |  |
5 | Grandes rombicuboctaedros no convexos | 40{3}
(30+60){4} |
240 | 120 | Ih | Th | |
| UC68 | disco |  |
2 | Cubos romos | (16+48){3}
12{4} |
120 | 48 | Oh | O | |
| UC69 | dissid |  |
2 | Dodecaedros romos | (40+120){3}
24{5} |
300 | 120 | Ih | I | |
| UC70 | giddasid |  |
2 | Grandes icosidodecaedros romos | (40+120){3}
24{5/2} |
300 | 120 | Ih | I | |
| UC71 | gidsid |  |
2 | Grandes icosidodecaedros romos invertidos | (40+120){3}
24{5/2} |
300 | 120 | Ih | I | |
| UC72 | gidrissid |  |
2 | Grandes icosidodecaedros retrorromos | (40+120){3}
24{5/2} |
300 | 120 | Ih | I | |
| UC73 | disdid |  |
2 | Dodecadodecaedros romos | 120{3}
24{5} 24{5/2} |
300 | 120 | Ih | I | |
| UC74 | idisdid |  |
2 | Dodecadodecaedros romos invertidos | 120{3}
24{5} 24{5/2} |
300 | 120 | Ih | I | |
| UC75 | desided |  |
2 | Icosidodecadodecaedros romos | (40+120){3}
24{5} 24{5/2} |
360 | 120 | Ih | I |
Referencias
- .Skilling, John (1976), «Uniform Compounds of Uniform Polyhedra» [Compuestos Uniformes de Poliedros Uniformes], Mathematical Proceedings of the Cambridge Philosophical Society (en inglés) 79: 447-457, MR 0397554, doi:10.1017/S0305004100052440..
Enlaces externos
- Esta obra contiene una traducción derivada de «Uniform Polyhedron Compunds» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- http://www.interocitors.com/polyhedra/UCs/ShortNames.html - Acrónimos de Bowers para compuestos poliédricos uniformes