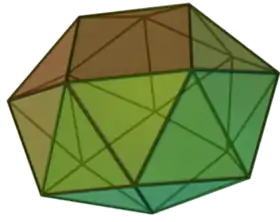
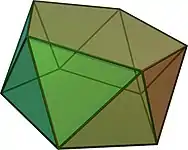
Simetría diédrica en tres dimensiones
En geometría, la simetría diédrica en tres dimensiones[1] es una de las tres secuencias infinitas de grupos de puntos en tres dimensiones que tienen un grupo de simetría que, como grupo abstracto, se corresponde con el grupo diedral Dihn (para n ≥ 2).
 Simetría involutiva Cs, (*) [ ] = |
 Simetría cíclica Cnv, (*nn) [n] = |
 Simetría diédrica Dnh, (*n22) [n,2] = | |
| Grupo poliédrico, [n,3], (*n32) | |||
|---|---|---|---|
 Simetría tetraédrica Td, (*332) [3,3] = |
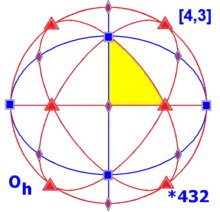 Simetría octaédrica Oh, (*432) [4,3] = |
 Simetría icosaédrica Ih, (*532) [5,3] = | |
Tipos
Hay 3 tipos de simetría diédrica en tres dimensiones, cada uno de los cuales se muestra a continuación en tres notaciones: la notación de Schönflies notation, la notación de Coxeter y la notación orbifold.
- Quiral
- Dn, [n,2]+, (22n) de orden 2n (o también simetría diédrica o grupo para-n-gonal'; el grupo abstracto: Dihn).
- Aquiral
- Dnh, [n,2], (*22n) de orden 4n (o también simetría prismática o grupo orto-n-gonal'; el grupo abstracto: Dihn × Z2).
- Dnd (o Dnv), [2n,2+], (2*n) de orden 4n (o también simetría antiprismática o grupo giro-n-gonal completo; el grupo abstracto: Dih2n).
Para un n dado, los tres tienen simetría rotacional multiplicada por n alrededor de un eje (un movimiento de rotación por un ángulo de 360°/n no cambia la disposición de los puntos del objeto), y simetría rotacional doble sobre un eje perpendicular (en consecuencia sobre estos n ejes). Para n = ∞, corresponden a tres frisos. Se utiliza la notación de Schoenflies, con la notación de Coxeter entre corchetes y la notación orbifold entre paréntesis. El término horizontal (h) se usa con respecto a un eje de rotación vertical.
En 2D, el grupo de simetría Dn incluye reflexiones en líneas rectas. Cuando el plano 2D está incrustado horizontalmente en un espacio 3D, tal reflexión puede verse como la restricción a ese plano de una reflexión a través de un plano vertical, o como la restricción al plano de una rotación alrededor de la línea de reflexión, por 180°. En 3D, se distinguen las dos operaciones: el grupo Dn contiene solo rotaciones, no reflexiones. El otro grupo es el de la simetría piramidal Cnv del mismo orden, 2n.
Con la simetría especular en un plano perpendicular al eje de rotación de n, se tiene Dnh, [n], (*22n).
Dnd (o Dnv), [2n,2+], (2*n) tiene planos de reflexión verticales entre los ejes de rotación horizontales, no a través de ellos. Como resultado, el eje vertical es un eje de rotación impropia de 2n.
Dnh es el grupo de simetría de un prisma regular de n lados y también para una bipirámide regular de n lados. Dnd es el grupo de simetría para un antiprisma regular de n lados, y también para un trapezoedro regular de n lados. Dn es el grupo de simetría de un prisma parcialmente girado.
No se incluye n = 1 porque las tres simetrías son iguales a otras:
- D1 y C2: grupo de orden 2 con una sola rotación de 180°.
- D1h y C2v: grupo de orden 4 con una reflexión en un plano y una rotación de 180° alrededor de una línea recta en ese plano.
- D1d y C2h: grupo de orden 4 con una reflexión en un plano y una rotación de 180° alrededor de una línea recta perpendicular a ese plano.
Para n = 2 no hay un eje principal y dos ejes adicionales, sino tres equivalentes.
- D2, [2,2]+, (222) de orden 4 es uno de los tres tipos de grupos de simetría con el grupo de Klein como grupo abstracto. Tiene tres ejes de rotación perpendiculares dobles. Es el grupo de simetría de un cuboide con una letra S marcada en dos caras opuestas, con la misma orientación.
- D2h, [2,2], (*222) de orden 8 es el grupo de simetría de un paralelepípedo.
- D2d, [4,2+], (2*2) de orden 8 es el grupo de simetría de por ejemplo:
- Un paralelepípedo cuadrado con una diagonal dibujada en una cara cuadrada y una diagonal perpendicular en la otra.
- Un tetraedro regular escalado en la dirección de una línea que conecta los puntos medios de dos aristas opuestas (D2d es un subgrupo de Td; al escalar la figura según una dirección se reduce la simetría).
Subgrupos
 D2h, [2,2], (*222) |
 D4h, [4,2], (*224) |
Para Dnh, [n,2], (*22n), orden 4n
- Cnh, [n+,2], (n*), orden 2n
- Cnv, [n,1], (*nn), orden 2n
- Dn, [n,2]+, (22n), orden 2n
Para Dnd, [2n,2+], (2*n), orden 4n
- S2n, [2n+,2+], (n×), orden 2n
- Cnv, [n+,2], (n*), orden 2n
- Dn, [n,2]+, (22n), orden 2n
Dnd también es un subgrupo de D2nh.
Ejemplos
| D2h, [2,2], (*222) Orden 8 |
D2d, [4,2+], (2*2) Orden 8 |
D3h, [3,2], (*223) Orden 12 |
|---|---|---|
 Costuras de un balón de baloncesto |
.png.webp) Costuras de una pelota de béisbol (ignorando la direccionalidad de la costura) |
 Balón de playa (ignorando los colores) |
|
Dnh, [n], (*22n):
|
D5h, [5], (*225):
|
D4d, [8,2+], (2*4):
|
|
D5d, [10,2+], (2*5):
|
D17d, [34,2+], (2*17):
|
Véase también
Referencias
- Norman L. Biggs, Professor of Mathematics London School of Economics Norman L Biggs (2002). Discrete Mathematics. OUP Oxford. pp. 392 de 425. ISBN 9780198507178. Consultado el 22 de agosto de 2022.
Bibliografía
- Harold Scott MacDonald Coxeter, H. S. M. and Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.
- N.W. Johnson: Geometrías y transformaciones, (2018) ISBN 978-1-107-10340-5 Capítulo 11: Grupos de simetría finita, 11.5 Grupos esféricos de Coxeter
- Conway, John Horton; Huson, Daniel H. (2002), «The Orbifold Notation for Two-Dimensional Groups», Structural Chemistry (Springer Netherlands) 13 (3): 247-257, doi:10.1023/A:1015851621002.
Enlaces externos
- Resumen gráfico de los 32 grupos de puntos cristalográficos: forme las primeras partes (aparte de omitir n=5) de las 7 series infinitas y 5 de los 7 grupos de puntos 3D separados