Compuesto de cinco tetraedros
El compuesto de cinco tetraedros es uno de los cinco compuestos poliédricos regulares. Este poliedro compuesto es también una estelación del icosaedro regular. Fue descrito por primera vez por Edmund Hess en 1876. También puede considerarse como el facetado de un dodecaedro regular.
| Compuesto de cinco tetraedros | |
|---|---|
 | |
| Tipo | Compuesto regular |
| Símbolo de Coxeter | {5,3}[5{3,3}] {3,5}[1] |
| Índice | UC5, W24 |
| Elementos (Como un compuesto) | 5 tetraedros: F= 20, E= 30, V= 20 |
| Compuesto dual | Autodual |
| Grupo de simetría | Icosaédrica quiral (I) |
| Subgrupo restringido de un miembro | Tetraédrico quiral (T) |
.stl.png.webp)
Como un compuesto
Se puede construir disponiendo cinco tetraedros de acuerdo con una simetría icosaédrica (I), como se colorea en el modelo superior de la derecha. Es uno de los cinco compuestos regulares que se pueden construir a partir de sólidos platónicos idénticos.
Comparte la misma disposición de vértices que un dodecaedro regular.
Hay dos formas enantiomorfas (la misma figura pero con quiralidad opuesta) de este poliedro compuesto. Ambas formas juntas crean el compuesto de diez tetraedros, especularmente simétrico.
Tiene un densidad superior a 1.
 Como un poliedro esférico |
 Modelo transparente (animación) |
 Cinco tetraedros entrelazados |
Como una estelación
También se puede obtener mediante la estelación de un icosaedro, y como tal figura en el índice de modelos de Wenninger con el número 24.
| Diagrama de estelación | Núcleo de la estelación | Envolvente convexa |
|---|---|---|
 |
 Icosaedro |
 Dodecaedro |
Como un facetado

Es un facetado de un dodecaedro, como se muestra en la imagen de la izquierda.
Teoría de grupos
El compuesto de cinco tetraedros es una ilustración geométrica de la noción de órbitas y estabilizadores, como se explica a continuación.
El grupo de simetría del compuesto es la simetría icosaédrica I (rotacional) de orden 60, mientras que el estabilizador de un solo tetraedro elegido es la simetría tetraédrica T (rotacional) de orden 12, y el espacio de la órbita I/T (de orden 60/12 = 5) se identifica naturalmente con los 5 tetraedros - la clase lateral gT corresponde a aquella en la que el tetraedro g se corresponde con el tetraedro elegido.
Una propiedad dual inusual

Este compuesto es inusual, ya que su figura dual es la quiral de la original. Si las caras están giradas a la derecha, entonces los vértices están girados a la izquierda. Cuando se genera el dual, las caras se corresponden con vértices girando a la derecha, y los vértices se corresponden con caras girando a la izquierda, obteniéndose una figura gemela quiral. Las figuras con esta propiedad son extremadamente raras.
Véase también
Referencias
- Regular polytopes, p.98
Bibliografía
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- H.S.M. Coxeter, Regular Polytopes, (3ra edición, 1973), edición de Dover, ISBN 0-486-61480-8, 3.6 Los cinco compuestos regulares, pp.47-50, 6.2 Estrellando los sólidos platónicos, pp.96 -104
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty nine icosahedra (3rd edición). Tarquin. ISBN 978-1-899618-32-3. MR 676126. (primera edición de la Universidad de Toronto (1938))
Enlaces externos
- Weisstein, Eric W. «Tetrahedron 5-Compound». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Escultura de metal del compuesto de cinco tetraedros
- Modelo VRML:
- Compuestos de 5 y 10 tetraedros por Sándor Kabai, Wolfram Demonstrations Project.
- Klitzing Polytopes (compuesto 3D)
| Estelaciones notables del icosaedro | |||||||||
| Regulares | Duales uniformes | Compuestos regulares | Estrella regular | Otros | |||||
| Icosaedro (convexo) | Pequeño icosaedro triámbico | Mediano icosaedro triámbico | Gran icosaedro triámbico | Compuesto de cinco octaedros | Compuesto de cinco tetraedros | Compuesto de diez tetraedros | Gran icosaedro | Dodecaedro excavado | Estelación final |
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 | |
 |
 |
 |
 |
 |
 |
 |
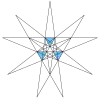 |
 | |
| El proceso de estelación en el icosaedro crea una serie de poliedros y compuestos relacionados con simetría icosaédrica | |||||||||