Gran icosaedro triámbico
En geometría, el gran icosaedro triámbico y el mediano icosaedro triámbico (o icosaedro triámbico medio) son dos poliedros uniformes duales entre sí, visualmente idénticos. La superficie exterior también representa la estelación De2f2 del icosaedro. Estas figuras se pueden diferenciar marcando qué intersecciones entre aristas son verdaderos vértices y cuáles no. En las imágenes de arriba, los vértices verdaderos están marcados por esferas doradas, que se pueden ver en las áreas cóncavas en forma de Y. Alternativamente, si las caras se rellenan según la regla par-impar, la estructura interna de ambas formas diferirá.
| Gran icosaedro triámbico | Mediano icosaedro triámbico | |
 |
 | |
| Tipos | Poliedro uniforme dual | |
| Grupo de simetría | Ih | |
| Nombre | Gran icosaedro triámbico | Mediano icosaedro triámbico |
| Índices de referencia | DU47, W34, 30/59 | DU41, W34, 30/59 |
| Elementos | F= 20, E= 60 V= 32 (χ= -8) | F= 20, E= 60 V= 24 (χ= -16) |
| Caras isoedrales | 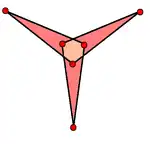 |  |
| Duales |  Gran icosidodecaedro ditrigonal |  Dodecadodecaedro ditrigonal |
| Estelación | ||
| Icosaedro: W34 | ||
 Diagrama de estelación | ||

.stl.png.webp)
Los 12 vértices de su envolvente convexa coinciden con la disposición de vértices de un icosaedro.
Gran icosaedro triámbico
El gran icosaedro triambico es el dual del gran icosidodecaedro ditrigonal, U47. Tiene 20 caras hexagonales invertidas (triambos), con una forma similar a la de una hélice de tres palas. Tiene 32 vértices (12 puntos exteriores y 20 ocultos en el interior), y un total 60 aristas.
Las caras tienen ángulos alternos de y . La suma de los seis ángulos es , y no como cabría esperar de un hexágono, porque el polígono gira alrededor de su centro dos veces. Su ángulo diedro es igual a .
Mediano icosaedro triámbico
El mediano icosaedro triambico es el dual del dodecadodecaedro ditrigonal, U41. Tiene 20 caras, cada una de las cuales es de forma cóncava simple isotoxal hexagonal o triámbica. Tiene 24 vértices (12 puntos exteriores y 12 ocultos en el interior), y un total de 60 aristas.
Las caras tienen ángulos alternos de y . Su ángulo diedro es igual a .
A diferencia del gran icosaedro triámbico, el mediano icosaedro triámbico es topológicamente un poliedro regular de índice dos.[1] Al distorsionar las formas triámbicas en hexágonos regulares, se obtiene como espacio cociente un teselado hexagonal de orden-5 hiperbólico:

Como una estelación


Es el modelo 34 de Magnus Wenninger, en cuya relación de poliedros figura como la novena estelación del icosaedro
Referencias
- The Regular Polyhedra (of index two) Archivado el 4 de marzo de 2016 en Wayback Machine., David A. Richter
Bibliografía
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 730208.
- H.S.M. Coxeter, Regular Polytopes, (3ra edición, 1973), edición de Dover, ISBN 0-486-61480-8, 3.6 6.2 Estelando los sólidos platónicos, pp.96-104
Enlaces externos
- Weisstein, Eric W. «Great triambic icosahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Medial triambic icosahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- gratrix.net Poliedros uniformes y duales
- bulatov.org Icosaedro triámbico medial Gran icosaedro triámbico
| Estelaciones notables del icosaedro | |||||||||
| Regulares | Duales uniformes | Compuestos regulares | Estrella regular | Otros | |||||
| Icosaedro (convexo) | Pequeño icosaedro triámbico | Mediano icosaedro triámbico | Gran icosaedro triámbico | Compuesto de cinco octaedros | Compuesto de cinco tetraedros | Compuesto de diez tetraedros | Gran icosaedro | Dodecaedro excavado | Estelación final |
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 | |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| El proceso de estelación en el icosaedro crea una serie de poliedros y compuestos relacionados con simetría icosaédrica | |||||||||