Función de Clausen
En matemáticas, la función de Clausen, introducida por Thomas Clausen en 1832, es una función especial transcendental de una sola variable.
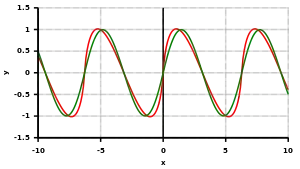
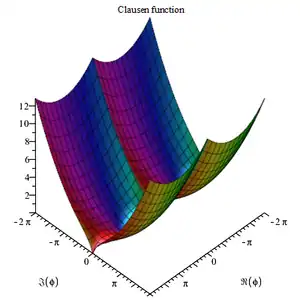
Se puede expresar en la forma de una integral definida, de una serie trigonométrica y a partir de otras funciones especiales. Está conectada íntimamente con el polilogaritmo, la integral de la tangente inversa, la función poligamma, la función zeta de Riemann, la función eta de Dirichlet y la función beta de Dirichlet.
La función de Clausen de orden 2, frecuentemente referida como la «función de Clausen», siendo una de sus muchas clases, viene dada por la integral:
En el rango , la función seno carece del signo de valor absoluto por ser estrictamente positiva, de manera que el símbolo del valor absoluto puede omitirse.
La función de Clausen también se puede representar en serie de Fourier:
Las funciones Clausen, como una clase de funciones, se utilizan ampliamente en numerosas áreas de investigación de la matemática moderna, sobre todo en relación con la evaluación de muchas clases de integrales logarítmicas y polilogarítmicas, tanto definidas como indefinidas. También tienen diversas aplicaciones para el cálculo de series hipergeométricas, sumas que impliquen la inversa del coeficiente binomial central, sumas de la función poligamma y series L de Dirichlet.
Propiedades básicas
La función de Clausen (de orden 2) tiene ceros simples en todo (número entero) múltiplo de ya que si es un número entero, :
Tiene un máximo en:
y un mínimo en:
Las siguientes propiedades son consecuencia inmediata de la definición de serie:[1]
Definición general
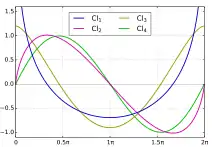
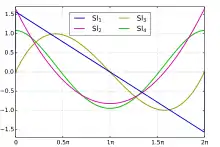
Con un carácter más amplio, se definen las dos funciones generalizadas de Clausen:
que son válidas en el campo complejo z con Re z >1. La definición se puede extender a todo el plano complejo a través de su extensión analítica.
Cuando z es reemplazado por un número entero no-negativo, las funciones estándar de Clausen se definen mediante la serie de Fourier siguiente:
Cabe notar que las funciones de Clausen de tipo SL tienen la notación alternativa y se denominan en ocasiones como las funciones de Glaisher-Clausen (de James Whitbread Lee Glaisher, de ahí la notación GL).
Relación con los polinomios de Bernoulli
Las funciones de Clausen del tipo SL son polinomiales en , y están estrechamente relacionadas con los polinomios de Bernoulli. Esta conexión se desprende de las representaciones de la serie de Fourier de los polinomios de Bernoulli:
Configurando en la expresión anterior y reordenando después los términos resultan las siguientes expresiones (polinomiales) de forma cerrada:
donde los polinómios de Bernoulli se definen en función de los números de Bernoulli por la relación:
Las ecuaciones explícitas deducidas de las anteriores incluyen:
Fórmula de duplicación
Para , se puede probar directamente la fórmula de duplicación en la definición de integral:[1]
Las consecuencias immediatas de la fórmula de duplicación, junto con el uso del valor especial , incluyen las relaciones:
Para las funcions de Clausen de orden superior, las fórmulas de duplicación se pueden obtener de la expuesta anteriormente; simplemente sustituyendo con la variable libre e integrando en el intervalo Aplicando el mismo proceso repetidamente, se tiene que:
Y más en general, con la inducción de
El uso generalizado de la fórmula de duplicación permite una extensión del resultado de la función de Clausen de orden 2, relacionándola con la constante de Catalan. Para
Donde es la función beta de Dirichlet.
Demostración de la fórmula de duplicación
A partir de la definición integral,
y aplicando la fórmula de duplicación de la funció seno, , se obtiene
Aplicando la sustitución en las dos integrales:
En esta última integral, substituyendo y utilizando la identidad trigonométrica , se puede ver que:
Por tanto,
Derivadas de las funciones de Clausen de orden general
Derivando directamente los desarrollos en serie de Fourier de las funciones de Clausen, se obtiene:
Aplicando el primer teorema fundamental del cálculo, también se tiene que:
Relación con la integral de la tangente inversa
Se define la integral de la tangente inversa en el intervalo con
Tiene la siguiente forma cerrada en términos de la función de Clausen:
Demostración de la relación con la integral de la tangente inversa
De la definición de la integral de la tangente inversa, se tiene
Realizando una integración por partes
Aplicando las sustituciones se obtiene
En la última integral, se debe aplicar la transformación y se consigue
Finalmente, como con la prueba de la fórmula de duplicación, la sustitución reduce esta última parte de la integral a
así
Relación con la función G-Barnes
Para los números reales , la función de Clausen de orden 2 se puede expresar en términos de la función G-Barnes y la función Gamma (de Euler):
o de forma equivalente[2]
Relación con el polilogaritmo
Las funciones de Clausen representen las partes real e imaginaria del polilogaritmo en la circunferencia unidad:
También se puede comprobar fácilmente acudiendo a la definición de la serie del polilogaritmo.
Por el teorema de Euler,
y por el teorema de De Moivre (fórmula de De Moivre)
por tanto
Relación con la función poligamma
Las funciones de Clausen están íntimamente relacionadas con la función poligamma. De hecho, es posible expresar las funciones de Clausen con combinaciones lineales de funciones de senos y de la función poligamma. Una de estas relaciones se demuestra a continuación:
Sean i dos números enteros positivos, tal que es un número racional y, a continuación, por la definición de las series para la función de orden superior de Clausen (de índice par):
se divide este sumatorio exactamente en p partes, de manera que la primera serie contenga todos, y no más, los términos congruentes con la segunda serie contiene todos los términos congruentes con etc., quedando la parte final de orden p, que contiene todos los términos congruentes con
Se pueden indexar estos sumatorios para formar una sumatorio doble:
Aplicando la fórmula de adición para la función seno, el término sinusoidal en el numerador se convierte en:
y como consecuencia
Para convertir el sumatorio interior del doble sumatorio en una suma no alterna, se divide exactamente en dos partes de la misma manera que el sumatorio interior anterior se dividió en p partes:
Para , la función poligamma se puede representar con la serie
Por tanto, en términos de la función poligamma, el sumatorio anterior se convierte en:
Aplicando este término en el sumatorio doble, se obtiene el resultado deseado
Relación con la integral log-seno generalizada
La integral log-seno generalizada se define por:
En esta notación generalizada, la función de Clausen se puede expresar en la forma:
Relación con la función de Lobachewsky
La función de Lobachevski (Λ o Л) es esencialmente la misma función con un cambio de variable:
aunque históricamente el nombre de «función de Lobachevski» no es del todo precisa, dado que las fórmules de Lobachevski para el volumen hiperbólico que utilicen la función ligeramente diferente
Relación con las series L de Dirichlet
Para los valores racionales de (es decir, para con los números enteros p i q), la función puede ser utilizada para representar una órbita periódica de un elemento en el grupo cíclico, y por tanto se puede expresar con una simple suma que implica la función zeta de Hurwitz. También permite que las relaciones entre ciertas series L de Dirichlet se puedan calcular fácilmente.
Aceleración de la serie
Una aceleración de la serie para la función de Clausen viene dada por
válida para . Aquí, { es la función zeta de Riemann. Una forma de convergencia más rápida viene dada por
El factor ayuda a la convergencia acercándola rápidamente a cero para valores grandes de n.[3]
Valores especiales
Algunos valores especiales incluyen
Valores especiales generalizados
Algunos valores especiales para funciones de Clausen de orden superior incluyen
donde es la constante de Catalan, es la función beta de Dirichlet, es la función eta de Dirichlet, y es la función zeta de Riemann.
Integrales de la función directa
Las siguientes integrales se demuestran fácilmente a partir de las representaciones de la serie de la función de Clausen:
Evaluación de integrales que implican la función directa
Un gran número de las integrales trigonométricas y logaritmo-trigonométricas pueden ser evaluadas en términos de la función de Clausen, y diversas constantes matemáticas comunes con (constante de Catalan), , y los casos especiales de la función zeta, i .
Los ejemplos que figuran a continuación son una consecuencia directa de la representación integral de la función de Clausen, y sus demostraciones requieren poco más que trigonometría básica, la integración por partes, y la integración ocasional término a término de las definiciones de las series de Fourier de las funciones de Clausen.
Referencias
Bibliografía
- Abramowitz, Milton; Stegun, Irene Ann (1964). "Chapter 27.8". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (en inglés). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards: Dover Publications. p. 1005. ISBN 978-0-486-61272-0.
- Adamchik, Viktor S (2003). Contributions to the Theory of the Barnes Function (en inglés).
- Borwein, Jonathan M; Bradley, David M; Crandall, Richard E (2000). Computational Strategies for the Riemann Zeta Function (en inglés). J. Comp. App. Math. 121. p. 247–296. doi:10.1016/s0377-0427(00)00336-8.
- Borwein, Jonathan M; Straub, Armin (2013). Relations for Nielsen Polylogarithms (en inglés). J. Approx. Theory. 193. p. 74-88. doi:10.1016/j.jat.2013.07.003.
- Clausen, Thomas (1832). Über die Function sin f + (1/22) sin 2f + (1/32) sin 3f + etc (en alemán). Journal für die reine und angewandte Mathematik. 8. p. 298-300. ISSN 0075-4102
- Kalmykov, Mikahil Yu; Sheplyakov, A (2005). LSJK – a C++ library for arbitrary-precision numeric evaluation of the generalized log-sine integral (en inglés). Comput. Phys. Comm. 172. p. 45–59. doi:10.1016/j.cpc.2005.04.013.
- Kölbig, Kurt Siegfried (1995). Chebyshev coefficients for the Clausen function Cl2(x) (en inglés). J. Comput. Appl. Math. 64 (3). p. 295-297. doi:10.1016/0377-0427(95)00150-6.
- Lewin, Leonard (1991). Structural Properties of Polylogarithms (en inglés). Providence, RI: American Mathematical Society. ISBN 0-8218-4532-2.
- Lu, Hung Jung; Perez, Christopher A (1992). Massless one-loop scalar three-point integral and associated Clausen, Glaisher, and L-functions (en inglés).
- Mathar, R. J (2013). A C99 implementation of the Clausen sums (en inglés).
- Wood, Van E (1968). Efficient calculation of Clausen's integral (en inglés). Math. Comp. 22 (104). p. 883-884. doi:10.1090/S0025-5718-1968-0239733-9.