Geometría de las transformaciones
La geometría de las transformaciones (o geometría transformacional) se refiere a una teoría pedagógica acerca de la enseñanza de la geometría euclídea que tiene como base el Programa de Erlangen, propuesto por el matemático alemán Felix Klein (1849-1925). Enfoca el estudio de la geometría centrándose en el concepto de los grupos de transformaciones geométricas, y en sus propiedades invariantes subyacentes. Se opone al enfoque clásico de la geometría sintética de euclídea, que se centra en la demostración de teoremas.

Por ejemplo, dentro de la geometría de las transformaciones, las propiedades de un triángulo isósceles se deducen del hecho de que una reflexión permite asignarse a sí mismo respecto a una determinada recta. Esto contrasta con las pruebas clásicas según los criterios como la congruencia de triángulos.[1]
Origen
El primer esfuerzo sistemático para usar las transformaciones como la base de la geometría fue realizado por Felix Klein en el siglo XIX, bajo el nombre de Programa de Erlangen. Durante casi un siglo, este enfoque se limitó a los círculos de investigación matemática. En el siglo XX se hicieron esfuerzos para explotarlo como base de la educación matemática. Andréi Kolmogórov incluyó este enfoque (junto con la teoría de conjuntos) como parte de una propuesta para la reforma de la enseñanza de la geometría en Rusia.[2] Estos esfuerzos culminaron en la década de 1960 con la reforma general de la enseñanza de las matemáticas conocida como el movimiento de la matemática moderna.
Pedagogía
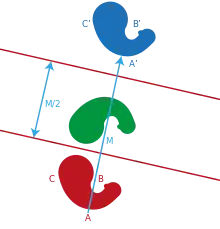
Una exploración de la geometría de las transformaciones a menudo comienza con un estudio de las simetrías que se encuentra en la vida diaria. La primera transformación real es la reflexión respecto a una recta o reflexión respecto a un eje. La composición de dos reflexiones da como resultado un movimiento de rotación cuando las líneas se intersecan, o una traslación cuando son paralelas. Así a través de las transformaciones los alumnos aprenden sobre la isometría afín. Por ejemplo, si se considera la reflexión respecto a una línea vertical y a una línea inclinada a 45° con respecto a la horizontal, se puede observar que una composición produce un cuarto de giro en sentido antihorario (90°), mientras que la composición inversa produce un cuarto de giro en el sentido de las agujas del reloj. Tales resultados muestran que la geometría de las transformaciones incluye procesos conmutativos.
Una curiosa aplicación de la reflexión respecto a una línea se da en la construcción del triángulo de un séptimo del área a partir de cualquier triángulo.
Otra transformación explicada a los jóvenes estudiantes es el escalado de las figuras. Sin embargo, la reflexión respecto a un círculo parece inapropiada para los grados más bajos. Por lo tanto, la geometría de inversión, un estudio más amplio que la geometría de transformación de la escuela primaria, suele reservarse para estudiantes universitarios.
Los experimentos con grupo de simetrías concretos dan paso a la teoría de grupos abstracta. Otras actividades concretas utilizan cálculos con número complejos, número hipercomplejos o matrices para expresar la geometría de las transformaciones.
Estas lecciones de geometría presentan una visión alternativa que contrasta con la geometría sintética clásica. Cuando los estudiantes se encuentran con la geometría analítica, las ideas de la rotación y la reflexión de coordenadas se comprenden fácilmente. Todos estos conceptos son la base del álgebra lineal, donde se expande el concepto de reflexión.
Los educadores han mostrado cierto interés y han descrito proyectos y experiencias con la geometría de las transformaciones para niños desde el jardín de infantes hasta la escuela secundaria. En el caso de los niños de muy corta edad, para evitar la introducción de una nueva terminología y establecer vínculos con la experiencia cotidiana de los estudiantes con objetos concretos, a veces se recomendaba usar palabras con las que están familiarizados, como reflejos para las reflexiones, marcos para las traslaciones, y giros para las rotaciones, aunque no se correspondan con un lenguaje matemático preciso. En algunas propuestas, los estudiantes comienzan con objetos concretos antes de realizar las transformaciones abstractas a través de sus definiciones de un aplicación de cada punto de la figura.[3][4][5][6]
En un intento por reestructurar los cursos de geometría en Rusia, Kolmogorov sugirió presentarlos bajo el punto de vista de las transformaciones, por lo que los cursos de geometría se estructuraron en base a la teoría de conjuntos. Esto llevó a la aparición en las escuelas del término congruentes para las cifras que antes se llamaban iguales: como una figura se veía como un conjunto de puntos, solo podía ser igual a sí misma y dos triángulos que pueden superponerse por isometrías se dice que son congruentes.[2]
Un autor expresó la importancia de la teoría de grupos para la geometría de transformación de la siguiente manera:
Me he tomado la molestia de desarrollar desde los primeros principios toda la teoría de grupos que necesito, con la intención de que mi libro pueda servir como una primera introducción a los grupos de transformación, y las nociones de la teoría de grupos abstracta si nunca la has visto.[7]
Artículos relacionados
Referencias
- Georges Glaeser – The crisis of geometry teaching
- Alexander Karp & Bruce R. Vogeli – Russian Mathematics Education: Programs and Practices, Volume 5, pgs. 100–102
- R.S. Millman – Kleinian transformation geometry, Amer. Math. Monthly 84 (1977)
- UNESCO - New trends in mathematics teaching, v.3, 1972 / pg. 8
- Barbara Zorin – Geometric Transformations in Middle School Mathematics Textbooks
- UNESCO - Studies in mathematics education. Teaching of geometry
- Miles Reid & Balázs Szendröi (2005) Geometry and Topology, pg. xvii, Cambridge University Press, ISBN 0-521-61325-6, MR 2194744
Bibliografía
- Georges Glaeser – La crisis de la enseñanza de la geometría
- Heinrich Guggenheimer (1967) Plane Geometry and Its Groups, Holden-Day.
- Roger Evans Howe & William Barker (2007) Continuous Symmetry: From Euclid to Klein, American Mathematical Society, ISBN 978-0-8218-3900-3 .
- Robin Hartshorne (2011) Review of Continuous Symmetry, American Mathematical Monthly 118:565–8.
- Roger Lyndon (1985) Groups and Geometry, #101 London Mathematical Society Lecture Note Series, Cambridge University Press ISBN 0-521-31694-4 .
- P.S. Modenov and A.S. Parkhomenko (1965) Geometric Transformations, translated by Michael B.P. Slater, Academic Press.
- George E. Martin (1982) Transformation Geometry: An Introduction to Symmetry, Springer Verlag.
- Isaak Yaglom (1962) Geometric Transformations, Random House (translated from the Russian).
- Max Jeger (1966) Transformation Geometry (translated from the German).
- Transformations teaching notes from Gatsby Charitable Foundation
- Kristin A. Camenga (NCTM's 2011 Annual Meeting & Exposition) - Transforming Geometric Proof with Reflections, Rotations and Translations. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). (enlace roto: enero de 2018)
- Nathalie Sinclair (2008) The History of the Geometry Curriculum in the United States, pps. 63-66.
- Zalman P. Usiskin and Arthur F. Coxford. A Transformation Approach to Tenth Grade Geometry, The Mathematics Teacher, Vol. 65, No. 1 (January 1972), pp. 21-30.
- Zalman P. Usiskin. The Effects of Teaching Euclidean Geometry via Transformations on Student Achievement and Attitudes in Tenth-Grade Geometry, Journal for Research in Mathematics Education, Vol. 3, No. 4 (Nov., 1972), pp. 249-259.
- A. N. Kolmogorov. Геометрические преобразования в школьном курсе геометрии, Математика в школе, 1965, N.º 2, pp. 24–29. (Geometric transformations in a school geometry course) (in Russian)
- Alton Thorpe Olson (1970). High School Plane Geometry Through Transformations: An Exploratory Study, Vol. I. University of Wisconsin--Madison.
- Alton Thorpe Olson (1970). High School Plane Geometry Through Transformations: An Exploratory Study, Vol II. University of Wisconsin--Madison.
- Z. P. Dienes & E. W. Golding (1970) La geometría a través de las transformaciones (3 volúmenes), Editorial Teide.