Grafo plano exterior
En teoría de grafos, un grafo plano exterior es un grafo que tiene una representación plana para la que todos los vértices pertenecen a la cara exterior del dibujo.


Los grafos planos externos se pueden caracterizar (análogamente al teorema de Wagner para grafos planos) por los dos menores prohibidos K4 y K2,3, o por sus invariantes de grafo de Colin de Verdière.
Poseen ciclos hamiltonianos si y solo si están biconectados, en cuyo caso la cara exterior forma el único ciclo hamiltoniano. Cada grafo plano externo tiene 3 colores; y degeneración y ancho de árbol como máximo 2.
Los grafos planos exteriores son un subconjunto de los grafos planos, de los subgrafos de grafos serie-paralelo y de los grafos circulares. Los grafos planos exteriores máximos, aquellos a los que no se les pueden añadir más aristas conservando la planaridad exterior, también son cordales y de visibilidad.
Historia
Los grafos planos exteriores fueron estudiados y nombrados por primera vez por Chartrand y Harary (1967), en relación con el problema de determinar la planaridad de los grafos formados mediante el uso de un emparejado perfecto para conectar dos copias de un grafo base (por ejemplo, muchos de los grafos de Petersen generalizados se forman de esta manera a partir de dos copias de un grafo ciclo). Como demostraron, cuando el grafo base es biconectado, un grafo construido de esta manera es plano si y solo si su grafo base es plano exterior y su emparejado forma una permutación diédrica de su ciclo exterior. Chartrand y Harary también demostraron un análogo al Teorema de Kuratowski para grafos planos exteriores, que afirma que un grafo es plano exterior si y solo si no contiene una subdivisión de uno de los dos grafos K4 o K2,3.
Definición y caracterizaciones
Un grafo plano exterior es un grafo que puede ser representado en el plano sin cruces de tal manera que todos los vértices pertenecen a la cara no acotada del dibujo. Es decir, ningún vértice está totalmente rodeado de aristas. Alternativamente, un grafo G es plano exterior si el grafo formado a partir de G mediante la adición de un nuevo vértice, con aristas que lo conectan con todos los demás vértices, es un grafo plano.[1]
Un grafo de plano exterior máximo es un grafo plano exterior al que no se le pueden agregar bordes adicionales mientras conserva la planaridad exterior. Todo grafo plano exterior máximo con n vértices tiene exactamente 2n − 3 aristas, y cada cara delimitada de un grafo plano exterior máximo es un triángulo.
Grafos prohibidos
Los grafos exteriores tienen una caracterización de grafos prohibidos análoga al teorema de Kuratowski y al teorema de Wagner para grafos planos: un grafo es exterior si y solo si no contiene una subdivisión del grafo completo K4 o el grafo bipartito completo K2,3.[2] Alternativamente, un grafo es plano exterior si y solo si no contiene K4 o K2,3 como menor (un grafo obtenido a partir de eliminar y contraer bordes).[3]
Un grafo sin triángulos es plano exterior si y solo si no contiene una subdivisión de K2,3.[4]
Invariantes de Colin de Verdière
Un grafo es plano exterior si y solo si su invariante de grafo de Colin de Verdière es como máximo dos. Los grafos caracterizados de manera similar por tener un invariante de Colin de Verdière como máximo de uno, tres o cuatro son respectivamente los bosques lineales, los grafos planos y los grafos embebidos sin enlaces.
Propiedades
Biconectividad y hamiltonicidad
Un grafo plano exterior es biconectado si y solo si la cara exterior del grafo forma un ciclo simple sin vértices repetidos. Un grafo plano exterior es hamiltoniano si y solo si es biconexo; en este caso, la cara exterior forma el único ciclo hamiltoniano.[5] De manera más general, el tamaño del ciclo más largo en un grafo plano exterior es el mismo que el número de vértices en su componente biconectado más grande. Por esta razón, encontrar ciclos hamiltonianos y ciclos más largos en grafos planos exteriores puede resolverse en tiempo lineal, en contraste con el carácter NP-completo de estos problemas para grafos arbitrarios.
Todo grafo plano exterior máximo satisface una condición más fuerte que la hamiltonicidad: es nodo pancíclico, lo que significa que para cada vértice v y para cada número k en el rango de tres al número de vértices en el grafo, hay un ciclo de longitud k que contiene a v. Se puede encontrar un ciclo de esta longitud quitando repetidamente un triángulo que esté conectado al resto del grafo por una sola arista, de modo que el vértice eliminado no sea v, hasta que la cara exterior del grafo restante tenga una longitud k.[6]
Un grafo plano es plano exterior si y solo si cada uno de sus componentes biconectados es plano exterior.[4]
Coloreado
Todos los grafos planos exteriores sin bucles pueden ser coloreados usando solo tres colores.[7] Este hecho ocupa un lugar destacado en la demostración simplificada por hallada por Fisk (1978) del problema de la galería de arte planteado por Václav Chvátal. Se puede encontrar un 3-coloreado en tiempo lineal mediante un algoritmo de coloreado ávido que elimina cualquier vértice de grado como máximo dos, colorea el grafo restante de forma recursiva y luego vuelve a agregar el vértice eliminado con un color diferente de los colores de sus dos vecinos.
De acuerdo con el teorema de Vizing, el índice cromático de cualquier grafo (el número mínimo de colores necesarios para colorear sus aristas para que no haya dos aristas adyacentes que tengan el mismo color) es el grado máximo de cualquier vértice del grafo o uno más el grado máximo. Sin embargo, en un grafo plano externo conexo, el índice cromático es igual al grado máximo excepto cuando el grafo forma un ciclo de longitud impar.[8] Se puede lograr una coloración de aristas con un número óptimo de colores y en tiempo lineal basado en una búsqueda transversal del árbol dual débil.[7]
Otras propiedades
Los grafos planos exteriores tienen degeneración como máximo dos: cada subgrafo de un grafo plano exterior contiene un vértice con grado como máximo dos.[9]
Los grafos planos exteriores tienen ancho de árbol como máximo dos, lo que implica que muchos problemas de optimización de grafos que son NP-completos para grafos arbitrarios pueden resolverse en tiempo lineal mediante programación dinámica cuando el grafo analizado es plano exterior. De forma más general, los grafos k-plano exteriores tienen un ancho de árbol O(k).[10]
Cada grafo plano exterior se puede representar como un grafo de intersección de rectángulos alineados con el eje en el plano, por lo que los grafos planos exteriores tienen cajeidad como máximo dos.[11]
Familias relacionadas de grafos
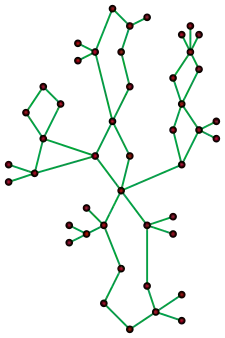
Todo grafo plano exterior es un grafo plano. Todo grafo plano exterior es también un subgrafo de un grafo serie-paralelo.[12] Sin embargo, no todos los grafos serie-paralelos planos son plano exteriores. El grafo bipartito completo K2,3 es plano y paralelo en serie pero no plano exterior. Por otro lado, el grafo completo K4 es plano pero no es serie-paralelo ni exterior. Cada bosque y cada grafo cactus son plano exteriores.[13]
El grafo plano dual débil de un grafo plano exterior incrustado (el grafo que tiene un vértice para cada cara acotada de la incrustación y una arista para cada par de caras acotadas adyacentes) es un bosque, y el plano dual débil de un grafo de Halin es un grafo plano exterior. Un grafo plano es plano exterior si y solo si su dual débil es un bosque, y es de Halin si y solo si su dual débil es biconexo y plano exterior.[14]
Hay una noción del grado de planaridad exterior. Una incrustación 1-plano exterior de un grafo es lo mismo que una incrustación en un plano exterior. Para k > 1, se dice que una incrustación plana es k-plano exterior si la eliminación de los vértices en la cara exterior da como resultado una incrustación plana exterior (k − 1).
Un grafo es k-plano exterior si tiene una incrustación k-plano exterior.[15]
Un grafo 1-plano exterior, de manera análoga a los grafos 1-planos, se puede dibujar en un disco, con los vértices en el límite del disco y con un cruce por borde como máximo.
Todo grafo plano exterior máximo es un grafo cordal. Todo grafo planar exterior máximo es el grafo de visibilidad de un polígono simple.[16] Los grafos planos exteriores máximos también se forman como grafos de triangulación de un polígono. Son ejemplos de 2-árboles, de grafos serie–paralelos y de grafos cordales.
Cada grafo plano exterior es un grafo circular, el grafo de intersección de un conjunto de cuerdas de una circunferencia.[17]
Referencias
- Felsner (2004).
- Chartrand y Harary (1967);Sysło (1979);Brandstädt, Le y Spinrad (1999), Proposition 7.3.1, p. 117;Felsner (2004).
- Diestel (2000).
- Sysło (1979).
- Chartrand y Harary (1967);Sysło (1979).
- Li, Corneil y Mendelsohn (2000), Proposition 2.5.
- Proskurowski y Sysło (1986).
- Fiorini (1975).
- Lick y White (1970).
- Baker (1994).
- Scheinerman (1984);Brandstädt, Le y Spinrad (1999), p. 54.
- Brandstädt, Le y Spinrad (1999), p. 174.
- Brandstädt, Le y Spinrad (1999), p. 169.
- Sysło y Proskurowski (1983).
- Kane y Basu (1976);Sysło (1979).
- El-Gindy (1985);Lin y Skiena (1995);Brandstädt, Le y Spinrad (1999), Theorem 4.10.3, p. 65.
- Wessel y Pöschel (1985);Unger (1988).
Bibliografía
- Baker, Brenda S. (1994), «Approximation algorithms for NP-complete problems on planar graphs», Journal of the ACM 41 (1): 153-180, S2CID 9706753, doi:10.1145/174644.174650..
- Boza, Luis; Fedriani, Eugenio M.; Núñez, Juan (2004), «The problem of outer embeddings in pseudosurfaces», Ars Combinatoria 71: 79-91..
- Boza, Luis; Fedriani, Eugenio M.; Núñez, Juan (2004), «Obstruction sets for outer-bananas-surface graphs», Ars Combinatoria 73: 65-77..
- Boza, Luis; Fedriani, Eugenio M.; Núñez, Juan (2006), «Uncountable graphs with all their vertices in one face», Acta Mathematica Hungarica 112 (4): 307-313, S2CID 123241658, doi:10.1007/s10474-006-0082-0..
- Boza, Luis; Fedriani, Eugenio M.; Núñez, Juan (2010), «Outer-embeddability in certain pseudosurfaces arising from three spheres», Discrete Mathematics 310 (23): 3359-3367, doi:10.1016/j.disc.2010.07.027..
- Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy (1999), Graph Classes: A Survey, SIAM Monographs on Discrete Mathematics and Applications, Sociedad de Matemáticas Aplicadas e Industriales, ISBN 0-89871-432-X, (requiere registro)..
- Chartrand, Gary; Harary, Frank (1967), «Planar permutation graphs», Annales de l'Institut Henri Poincaré B 3 (4): 433-438, MR 0227041..
- Diestel, Reinhard (2000), Graph Theory, Graduate Texts in Mathematics 173, Springer-Verlag, p. 107, ISBN 0-387-98976-5..
- El-Gindy, H. (1985), Hierarchical decomposition of polygons with applications, Ph.D. thesis, Universidad McGill.. Citado por Brandstädt, Le y Spinrad (1999).
- Felsner, Stefan (2004), Geometric graphs and arrangements: some chapters from combinational geometry, Vieweg+Teubner Verlag, p. 6, ISBN 978-3-528-06972-8..
- Fiorini, Stanley (1975), «On the chromatic index of outerplanar graphs», Journal of Combinatorial Theory, Series B 18 (1): 35-38, doi:10.1016/0095-8956(75)90060-X..
- Fisk, Steve (1978), «A short proof of Chvátal's watchman theorem», Journal of Combinatorial Theory, Series B 24 (3): 374, doi:10.1016/0095-8956(78)90059-X..
- Fleischner, Herbert J.; Geller, D. P.; Harary, Frank (1974), «Outerplanar graphs and weak duals», Journal of the Indian Mathematical Society 38: 215-219, MR 0389672..
- Kane, Vinay G.; Basu, Sanat K. (1976), «On the depth of a planar graph», Discrete Mathematics 14 (1): 63-67, doi:10.1016/0012-365X(76)90006-6..
- Li, Ming-Chu; Corneil, Derek G.; Mendelsohn, Eric (2000), «Pancyclicity and NP-completeness in planar graphs», Discrete Applied Mathematics 98 (3): 219-225, doi:10.1016/S0166-218X(99)00163-8..
- Lick, Don R.; White, Arthur T. (1970), «k-degenerate graphs», Canadian Journal of Mathematics 22 (5): 1082-1096, doi:10.4153/CJM-1970-125-1, archivado desde el original el 23 de julio de 2012, consultado el 14 de septiembre de 2022..
- Lin, Yaw-Ling; Skiena, Steven S. (1995), «Complexity aspects of visibility graphs», International Journal of Computational Geometry and Applications 5 (3): 289-312, doi:10.1142/S0218195995000179..
- Proskurowski, Andrzej; Sysło, Maciej M. (1986), «Efficient vertex-and edge-coloring of outerplanar graphs», SIAM Journal on Algebraic and Discrete Methods 7: 131-136, doi:10.1137/0607016..
- Scheinerman, E. R. (1984), Intersection Classes and Multiple Intersection Parameters of a Graph, Ph.D. thesis, Universidad de Princeton.. Citado por Brandstädt, Le y Spinrad (1999).
- Sysło, Maciej M. (1979), «Characterizations of outerplanar graphs», Discrete Mathematics 26 (1): 47-53, doi:10.1016/0012-365X(79)90060-8..
- Sysło, Maciej M.; Proskurowski, Andrzej (1983), «On Halin graphs», Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics 1018, Springer-Verlag, pp. 248-256, doi:10.1007/BFb0071635..
- Unger, Walter (1988), «On the k-colouring of circle-graphs», Proc. 5th Symposium on Theoretical Aspects of Computer Science (STACS '88), Lecture Notes in Computer Science 294, Springer-Verlag, pp. 61-72, doi:10.1007/BFb0035832..
- Wessel, W.; Pöschel, R. (1985), «On circle graphs», en Sachs, Horst, ed., Graphs, Hypergraphs and Applications: Proceedings of the Conference on Graph Theory Held in Eyba, October 1st to 5th, 1984, Teubner-Texte zur Mathematik 73, B.G. Teubner, pp. 207-210.. Citado por Unger (1988).
Enlaces externos
- Outerplanar graphs en el Sistema de información sobre clases de grafos y sus inclusiones
- Weisstein, Eric W. «Outplanar Graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.