Grafo serie-paralelo
En teoría de grafos, los grafos serie-paralelo son aquellos que poseen dos vértices especiales denominados terminales, y que están formados recursivamente por dos operaciones simples de composición. Se pueden utilizar para modelar circuitos eléctricos en serie y en paralelo.
Definición y terminología
En este contexto, el término grafo significa multigrafo.
Hay varias formas de definir grafos serie-paralelo. La siguiente definición básicamente sigue la utilizada por David Eppstein.[1]
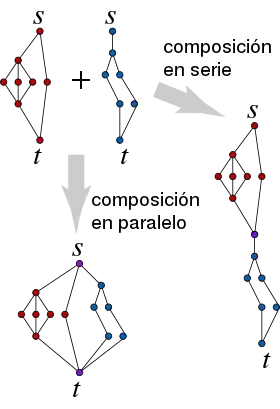
Un grafo de dos terminales (TTG) es un grafo con dos vértices distinguidos, s y t llamados fuente y sumidero, respectivamente.
La composición paralela Pc = Pc(X,Y) de dos TTG X e Y es un TTG creado a partir de la unión de grafos disjuntos X e Y fusionando las fuentes de X e Y para crear la fuente de Pc y fusionar los sumideros de X e Y para crear el sumidero de Pc.
La composición en serie Sc = Sc(X,Y) de dos TTGs X e Y es un TTG creado a partir de la unión disjunta de grafos X e Y fusionando el sumidero de X con la fuente de Y. La fuente de X se convierte en la fuente de Sc y el sumidero de Y se convierte en el sumidero de Sc.
Un grafo serie-paralelo de dos terminales (TTSPG) es un grafo que puede construirse mediante una secuencia de composiciones en serie y paralelo a partir de un conjunto de copias de un grafo de una sola arista K2 con terminales asignadas.
Definición 1. Finalmente, un grafo se denomina serie-paralelo (grafo-SP), si es un TTSPG cuando dos de sus vértices se consideran fuente y sumidero.
De manera similar, se pueden definir un digrafo en serie-paralelo, construido a partir de copias de grafos de un solo arco, con arcos dirigidos desde la fuente hasta el sumidero.
Definición alternativa
La siguiente definición especifica la misma clase de grafos.[2]
Definición 2. Un grafo es un grafo SP, si puede convertirse en K2 mediante una secuencia de las siguientes operaciones:
- Reemplazo de un par de aristas paralelas por una sola arista que conecta sus puntos finales comunes.
- Reemplazo de un par de aristas incidentes a un vértice de grado 2 que no sea s o t por una sola arista.
Propiedades
Cada grafo en serie-paralelo tiene ancho de árbol como máximo 2 y ancho de rama como máximo 2.[3] De hecho, un grafo tiene un ancho de árbol como máximo 2 si y solo si tiene un ancho de rama como máximo 2, si y solo si todo componente biconectado es un grafo en serie-paralelo.[4][5] Los grafos en serie-paralelo maximales, grafos a los que no se pueden agregar aristas adicionales sin destruir su estructura de serie-paralelo, son exactamente los 2-árboles.
Los grafos en serie-paralelo 2-conectados se caracterizan por no tener un subgrafo homeomorfo a K4.[3]
Los grafos serie-paralelo también se pueden caracterizar por su descomposición en orejas.[1]
Complejidad computacional
Los grafos SP pueden reconocerse en tiempo lineal[6] y su descomposición en serie-paralelo también puede construirse en tiempo lineal.
Además de ser un modelo de ciertos tipos de redes eléctricas, estos grafos son de interés en teoría de la complejidad computacional, porque una serie de problemas de grafos estándar se pueden resolver en tiempo lineal en grafos SP,[7] incluida la búsqueda de emparejamiento máximo, de conjuntos independientes, de conjuntos dominantes y de completamiento hamiltoniano. Algunos de estos problemas son NP-completos para grafos generales. La solución aprovecha el hecho de que si se conocen las respuestas de uno de estos problemas para dos grafos SP, entonces se puede encontrar rápidamente la respuesta para sus composiciones en serie y en paralelo.
Generalización
Los grafos serie-paralelo generalizados (grafos GSP) son una extensión de los grafos SP[8] con la misma eficiencia algorítmica para los problemas mencionados. La clase de grafos GSP incluye las clases de grafos SP y los grafos planos exteriores.
Los grafos GSP pueden especificarse mediante la Definición 2 aumentada con la tercera operación de eliminación de un vértice colgante (vértice de grado 1). Alternativamente, la Definición 1 puede complementarse con la siguiente operación.
- La combinación de fuentes S = M(X,Y) de dos TTG X e Y es un TTG creado a partir de la unión disjunta de grafos X e Y fusionando la fuente de X con la fuente de Y. La fuente y el sumidero de X se convierten en la fuente y el sumidero de P respectivamente.
Un árbol SPQR es una estructura de árbol que se puede definir para un grafo 2-vértices-conectado arbitrario. Tiene S nodos, que son análogos a las operaciones de composición en serie sobre grafos serie-paralelos; nodos P, que son análogos a las operaciones de composición en paralelo sobre grafos en serie-paralelo; y nodos R, que no corresponden a operaciones de composición sobre grafos en serie-paralelo. Un grafo conectado en 2 es serie-paralelo si y solo si no hay nodos R en su árbol SPQR.
Véase también
- Grafo umbral
- Cografo
- Politopo de Hanner
- Orden parcial serie-paralelo
Referencias
- Eppstein, David (1992). «Parallel recognition of series–parallel graphs». Information and Computation 98 (1): 41-55. doi:10.1016/0890-5401(92)90041-D.
- Duffin, R. J. (1965). «Topology of Series–Parallel Networks». Journal of Mathematical Analysis and Applications 10 (2): 303-313. doi:10.1016/0022-247X(65)90125-3.
- Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy P. (1999). Graph classes: a survey. SIAM Monographs on Discrete Mathematics. and Applications 3. Philadelphia, PA: Sociedad de Matemáticas Aplicadas e Industriales. pp. 172–174. ISBN 978-0-898714-32-6. Zbl 0919.05001.
- Bodlaender, H. (1998). «A partial k-arboretum of graphs with bounded treewidth». Theoretical Computer Science 209 (1–2): 1-45. doi:10.1016/S0304-3975(97)00228-4. hdl:1874/18312.
- Hall, Rhiannon; Oxley, James; Semple, Charles; Whittle, Geoff (2002). «On matroids of branch-width three». Journal of Combinatorial Theory, Series B 86 (1): 148-171. doi:10.1006/jctb.2002.2120.
- Valdes, Jacobo; Tarjan, Robert E.; Lawler, Eugene L. (1982). «The recognition of series parallel digraphs». SIAM Journal on Computing 11 (2): 289-313. doi:10.1137/0211023.
- Takamizawa, K.; Nishizeki, T.; Saito, N. (1982). «Linear-time computability of combinatorial problems on series–parallel graphs». Journal of the ACM 29 (3): 623-641. S2CID 16082154. doi:10.1145/322326.322328.
- Korneyenko, N. M. (1994). «Combinatorial algorithms on a class of graphs». Discrete Applied Mathematics 54 (2–3): 215-217. doi:10.1016/0166-218X(94)90022-1. Translated from Notices of the BSSR Academy of Sciences, Ser. Phys.-Math. Sci., (1984) no. 3, pp. 109–111 (en ruso)