Embebido sin enlaces
En teoría de grafos topológica, un embedido sin enlaces de un grafo es una incrustación del grafo en un espacio euclídeo tridimensional de tal manera que no hay dos ciclos del grafo enlazados entre sí. Un embedido plano es una incrustación con la propiedad de que cada ciclo es el límite de un disco topológico cuyo interior es disjunto con respecto al grafo. Un grafo embebible sin enlaces es un grafo que tiene un embedido plano o sin enlaces; estos grafos forman un análogo tridimensional de los grafos planos.[1] Complementariamente, un grafo vinculado intrínsecamente es un grafo que no tiene un embedido sin enlaces.

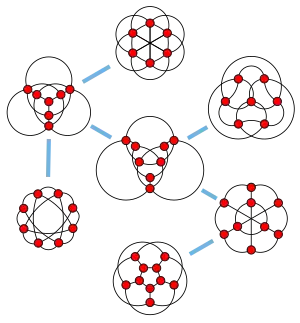
Los embebidos planos no tienen enlaces automáticamente, pero no al revés.[2] El grafo completo K6, el grafo de Petersen y los otros cinco grafos de la familia de Petersen no tienen embebidos sin enlaces.[1] Cada menor de un grafo integrable sin vínculos es nuevamente integrable sin vínculos,[3] al igual que cada grafo al que se puede llegar desde un grafo integrable sin enlaces mediante el teorema de Kennelly.[2] Los grafos integrables sin enlaces tienen los grafos de la familia de Petersen como sus menores prohibidos,[4] e incluyen los grafos planos y los grafos de ápice.[2] Se pueden reconocer, y se puede construir un empotramiento plano para ellos, en O(n2).[5]
Definiciones
Cuando un círculo se asigna a un espacio euclídeo tridimensional mediante una función inyectiva (una función continua que no asigna dos puntos diferentes del círculo al mismo punto del espacio), su imagen es una curva.
Dos curvas cerradas disjuntas que se encuentran ambas en el mismo plano están desenlazadas y, de manera más general, se dice que un par de curvas cerradas disjuntas están desvinculadas cuando existe una deformación continua del espacio capaz de mover ambas al mismo plano, sin que ninguna de las curvas atraviese a la otra o a sí misma. Si no existe tal movimiento continuo, se dice que las dos curvas están enlazadas. Por ejemplo, el enlace de Hopf está formado por dos aros que pasan cada uno por el disco interior del otro atravesándolo. Forma el ejemplo más simple de un par de curvas vinculadas, pero es posible que las curvas se vinculen de otras formas más complicadas. Si dos curvas no están vinculadas, entonces es posible encontrar un disco topológico en el espacio, teniendo la primera curva como su límite y disjunto de la segunda curva. Por el contrario, si existe tal disco, las curvas están necesariamente desvinculadas.
El número de enlace de dos curvas cerradas en el espacio tridimensional es un invariante topológico de las curvas: es un número, definido a partir de las curvas en cualquiera de varias formas equivalentes, que no cambia si las curvas se mueven continuamente sin cruzarse entre sí. La versión del número de enlace utilizada para definir embebidos de grafos sin enlaces se puede hallar proyectando el embedido sobre un plano y contando el número de veces que la primera curva cruza sobre la segunda, en módulo 2.[2] La proyección debe ser "regular", lo que significa que dos vértices no se pueden proyectar hacia el mismo punto, ningún vértice se proyecta hacia el interior de una arista, y en cada punto de la proyección donde se cruzan las proyecciones de dos aristas, se cruzan transversalmente. Con esta restricción, dos proyecciones cualesquiera conducen al mismo número de enlace.
El número de enlace de un modelo desvinculado es cero y, por lo tanto, si un par de curvas tiene un número de vinculación distinto de cero, las dos curvas deben estar enlazadas. Sin embargo, hay ejemplos de curvas que están enlazadas pero que tienen un número de enlace cero, como el eslabón de Whitehead.
Un embedido de un grafo en un espacio tridimensional consiste en una aplicación desde los vértices del grafo a puntos en el espacio, y desde los bordes del grafo a curvas en el espacio, de modo que cada punto final de cada borde se aplica a un punto final de la curva correspondiente, y tal que las curvas de dos aristas diferentes no se cortan excepto en un punto final común de las aristas.
Cualquier grafo finito tiene un número finito (aunque puede ser exponencial) de ciclos simples distintos, y si el grafo está embebido en un espacio tridimensional, cada uno de estos ciclos forma una curva cerrada simple. Se puede calcular el número de enlace de cada par de curvas disjuntas formadas de esta manera. Si todos los pares de ciclos tienen un número de enlace cero, se dice que el embedido no tiene enlaces.[6]
En algunos casos, un grafo puede estar incrustado en el espacio de tal manera que, para cada ciclo del grafo, se puede encontrar un disco delimitado por ese ciclo que no cruza a ningún otro elemento del grafo. En este caso, el ciclo debe estar desvinculado de todos los demás ciclos separados de él en el grafo. Se dice que el embedido es plano si cada ciclo limita un disco de esta manera.[7] Un embedido plano no tiene enlaces necesariamente, pero pueden existir embebidos sin enlaces que no son planos: por ejemplo, si G es un grafo formado por dos ciclos disjuntos, y está embebido para formar el enlace de Whitehead, entonces el embedido no tiene enlaces pero no es plano.
Se dice que un grafo está intrínsecamente enlazado si, independientemente de cómo esté embebido, el embedido resultante siempre está enlazado. Aunque los embebidos planos y sin enlaces no son lo mismo, los grafos que tienen embebidos sin enlaces son los mismos que los grafos que tienen embebidos planos.[8]
Ejemplos y contraejemplos
Como mostró Sachs (1983), cada uno de los siete grafos de la familia de Petersen están intrínsecamente enlazados: no importa cómo cada uno de estos grafos esté embebido en el espacio, siempre tienen dos ciclos que están vinculados entre sí. Estos grafos incluyen el grafo completo K6, el grafo de Petersen, el grafo formado al eliminar un borde del grafo bipartito completo K4,4 y el grafo tripartito completo K3,3,1.
Cada grafo plano tiene un embedido plano y sin enlaces: simplemente debe embeberse el grafo en un plano y embeber a su vez el plano en el espacio. Si un grafo es plano, esta es la única forma de embeberlo de forma plana y sin enlaces en el espacio: cada embedido plano puede deformarse continuamente para que quede en un plano. Y a la inversa, cada grafo sin enlaces no plano posee múltiples embebidos sin enlaces.[2]
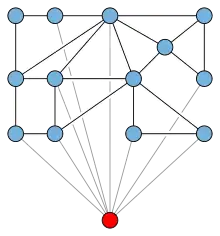
Un grafo de ápice, formado al agregar un solo vértice a un grafo plano, también tiene un embedido plano y sin enlaces: para comprobarlo, basta embeber la parte plana del grafo en un plano, colocar el ápice sobre el plano y dibujar las aristas desde el ápice hasta sus vecinos como segmentos de línea recta. Cualquier curva cerrada dentro del plano delimita un disco por debajo del plano que no pasa por ningún otro elemento del grafo, y cualquier curva cerrada a través del ápice delimita un disco por encima del plano que no pasa por ningún otro elemento del grafo.[2]
Si un grafo se puede transformar en un embedido plano o sin enlaces, entonces se puede modificar el grafo subdividiendo o dessubdividiendo sus aristas, agregando o eliminando múltiples aristas entre el mismo par de vértices y aplicando el teorema de Kennelly (que permite reemplazar un vértice de grado tres por un triángulo que conecta los tres vecinos o al revés), de manera que siempre se conserva la planitud y la ausencia de enlaces.[2] En particular, en un grafo plano cúbico (uno en el que todos los vértices tienen exactamente tres vecinos, como en un cubo) es posible hacer duplicados de cualquier conjunto independiente de vértices realizando transformaciones Y-Δ, agregando múltiples copias de los triángulos de aristas resultantes, y luego realizar las transformadas inversas Δ-Y.
Identificación y caracterización
Si un grafo G tiene un embedido plano o sin enlaces, entonces cada menor de G (un grafo formado por la contracción de las aristas y la eliminación de aristas y vértices) también tiene un embedido plano o sin enlaces. Las eliminaciones no pueden destruir la planitud de un embedido, y se puede realizar una contracción dejando un punto final del borde contraído en su lugar y redirigiendo todos los bordes incidentes a otro punto final en la ruta del borde contraído. Por lo tanto, por el teorema de Robertson–Seymour, los grafos integrables sin enlaces tienen una caracterización de grafo prohibida como los grafos que no contienen ningún elemento de un conjunto finito de menores.[3]
El conjunto de menores prohibidos para los grafos embebibles sin enlaces fue identificado por Sachs (1983): los siete grafos de la familia de Petersen son todos grafos menores-mínimos intrínsecamente vinculados. Sin embargo, Sachs no pudo probar que estos fueran los únicos grafos vinculados mínimos, aunque Robertson, Seymour y Thomas (1995) finalmente logró demostrarlo.
La caracterización menor prohibida de los grafos sin enlaces conduce a un algoritmo de tiempo lineal para su identificación, pero no para construir realmente un embedido.Kawarabayashi, Kreutzer y Mohar (2010) describió un algoritmo de tiempo lineal que comprueba si un grafo se puede embeber sin enlaces y, de ser así, construye un embedido plano del grafo. Su algoritmo encuentra grandes subgrafos planos dentro del grafo dado de tal manera que, si existe un embedido sin enlace, debe respetar el embedido plano del subgrafo. Al simplificar repetidamente el grafo cada vez que se encuentra un subgrafo de este tipo, reducen el problema a uno en el que el grafo restante ha acotado la anchura del árbol, en cuyo punto puede resolverse mediante un procedimiento de programación dinámica.Robertson, Seymour y Thomas (1993a) planteó el problema de comprobar de manera eficiente si un embedido dado es plano o sin enlaces. Sigue sin resolverse, y es equivalente en complejidad a un problema de desanudamiento, el problema de probar si una sola curva en el espacio no está anudada.[5] Se sabe que la prueba de ausencia de nudos (y, por lo tanto, también la prueba de falta de enlace de un embedido) es de dificultad NP, pero no se sabe que sea NP-completo.[9]
Familias relacionadas de grafos
El invariante de grafo de Colin de Verdière es un número entero definido para cualquier grafo definido mediante la teoría de grafos algebraicos. Los grafos con invariante de Colin de Verdière a lo sumo μ, para cualquier constante fija μ, forman una familia menor-cerrada, y los primeros son bien conocidos: los grafos con μ ≤ 1 son los bosques lineales (uniones disjuntas de caminos), los grafos con μ ≤ 2 son los grafos no planos, y los grafos con μ ≤ 3 son los grafos planos. Como conjeturó Robertson, Seymour y Thomas (1993a) y demostró Lovász y Schrijver (1998), los grafos con μ ≤ 4 son exactamente los grafos integrables sin enlaces.
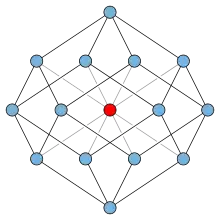
Los grafos planos y los grafos de ápice se pueden embeber sin enlaces, al igual que los grafos obtenidos por el teorema de Kennelly a partir de estos grafos.[2] Los grafos reducibles YΔY son aquellos que se pueden reducir a un solo vértice mediante transformadas Y-Δ, eliminación de vértices aislados y vértices de grado uno, y compresión de vértices de grado dos; también son cerrados menores e incluyen todos los grafos planos. Sin embargo, existen grafos sin enlaces que no son reducibles con YΔY, como el grafo de ápice formado al conectar el ápice a cada vértice de grado tres de un rombododecaedro.[10] También existen grafos sin enlaces que no se pueden transformar en un grafo de ápice mediante transformaciones Y-Δ, eliminación de vértices aislados y vértices de grado uno, y compresión de vértices de grado dos: por ejemplo, el grafo en corona de diez vértices tiene un embedido sin enlace, pero no se puede transformar en un grafo de ápice de esta manera.[2]
Relacionado con el concepto de embedido sin enlaces está el concepto de embebido sin nudos, un embedido de un grafo de tal manera que ninguno de sus ciclos simples forme un nudo no trivial. Los grafos que no tienen embebidos sin nudos (es decir, están intrínsecamente anudados) incluyen a K7 y a K3,3,1,1.[11] Sin embargo, también existen menores prohibidos mínimos para embebidos sin nudos que no se forman (como estos dos grafos) agregando un vértice a un grafo vinculado intrínsecamente.[12]
También se pueden definir familias de grafos por la presencia o ausencia de nudos y enlaces más complejos en sus embebidos,[13] o por embebidos sin enlaces en variedades tridimensionales que no sean el espacio euclídeo.[14] Flapan, Naimi y Pommersheim (2001) define un grafo embebido como triplemente enlazado si posee tres ciclos, ninguno de los cuales puede separarse de los otros dos; y demostraron que K9 no tiene un triple enlace intrínseco, pero K10 sí que lo tiene.[15] De manera más general, se puede definir un embedido n-enlazado para cualquier n como aquel que contiene un enlace de componente n que no puede dividirse mediante una esfera topológica en dos partes separadas. Se conocen grafos menores-mínimos intrínsecamente n-enlazados para todo n.[16]
Historia
La cuestión topológica de que si K6 tiene un embedido plano o sin enlaces, fue planteada dentro de la comunidad de investigadores por Bothe (1973) a principios de la década de 1970. Los embebidos sin enlaces llamaron la atención de la comunidad dedicada a la teoría de grafos gracias a Plantilla:Harvs, quien planteó varios problemas relacionados, incluido el problema de encontrar una caracterización de grafos prohibidos de los grafos con embebidos planos y sin enlaces. Sachs demostró que los siete grafos de la familia de Petersen (incluido K6) no tienen tales embebidos. Como observó Nešetřil y Thomas (1985), los grafos embebibles sin enlaces son cerrados bajo los menores de grafo, de lo cual se deduce por el teorema de Robertson-Seymour que existe una caracterización de grafos prohibidos. La prueba de la existencia de un conjunto finito de grafos de obstrucción no conduce a una descripción explícita de este conjunto de menores prohibidos, pero de los resultados de Sachs se sigue que los siete grafos de la familia de Petersen pertenecen al conjunto. Estos problemas fueron finalmente resueltos por Robertson, Seymour y Thomas (1995),[17] quienes demostraron que los siete grafos de la familia de Petersen son los únicos menores mínimos prohibidos para estos grafos. Por lo tanto, los grafos embebibles sin enlaces y los grafos embebibles planos son el mismo conjunto de grafos y son iguales a los grafos que no tienen menores de la familia de Petersen.Sachs (1983) también solicitó límites en el número de aristas y de colores para los grafos embebibles sin enlaces. El número de aristas en un grafo sin enlaces de n-vértices es como máximo 4n − 10: los grafos de ápice con n > 4 tienen exactamente esta cantidad máxima de aristas,[1] y Mader (1968) demostró que es un límite superior coincidente en la clase más general de grafos K6 libre de menores.Nešetřil y Thomas (1985) observó que la pregunta de Sachs sobre el número de colores se resolvería con una prueba de la conjetura de Hadwiger, que postula que cualquier grafo k-cromático tiene como menor un grafo completo de k vértices. La demostración dada por Robertson, Seymour y Thomas (1993c) del caso k = 6 de la conjetura de Hadwiger es suficiente para resolver la pregunta de Sachs: los grafos sin enlaces se pueden colorear con un máximo de cinco colores, ya que cualquier grafo 6-cromático contiene un K6 menor y no tiene enlaces, y existen grafos sin enlaces como K5 que requieren cinco colores. El teorema del snark implica que cada grafo integrable sin enlaces cúbico es 3-aristas-coloreable.
Los embebidos sin enlaces comenzaron a estudiarse dentro de la comunidad de investigación de algoritmos a finales de la década de 1980 a través de los trabajos de Fellows y Langston (1988) y Motwani, Raghunathan y Saran (1988). Algorítmicamente, el problema de reconocer grafos embebibles planos y sin enlaces se resolvió una vez que se demostró la caracterización del menor prohibido: se puede usar un algoritmo de Robertson y Seymour (1995) para probar en tiempo lineal si un grafo dado contiene alguno de los siete menores prohibidos.[18] Este método no construye incrustaciones planas o sin enlaces cuando existen, pero van der Holst (2009) desarrolló un algoritmo que construye un embedido, y Kawarabayashi, Kreutzer y Mohar (2010) encontró un algoritmo de tiempo lineal más eficiente.
Una pregunta final de Sachs (1983) sobre la posibilidad de un análogo del teorema de Fáry para grafos sin enlaces parece no haber sido respondida: ¿cuándo la existencia de un embedido plano o sin enlaces con bordes curvos o partes lineales implica la existencia de un embedido plano o sin enlaces en el que las aristas son segmentos rectos?
Véase también
Notas
- Sachs (1983).
- Robertson, Seymour y Thomas (1993a).
- Nešetřil y Thomas (1985)
- Robertson, Seymour y Thomas (1995).
- Kawarabayashi, Kreutzer y Mohar (2010)
- Conway y Gordon (1983);Sachs (1983);Robertson, Seymour y Thomas (1993a).
- Robertson, Seymour y Thomas (1993a). Una definición similar de "buena incrustación" figura en Motwani, Raghunathan y Saran (1988); véase también Saran (1989) y Böhme (1990).
- Robertson, Seymour y Thomas (1993b).
- Hass, Lagarias y Pippenger (1999).
- Truemper (1992).
- Conway y Gordon (1983);Foisy (2002).
- Foisy (2003).
- Nešetřil y Thomas (1985);Fleming y Diesl (2005).
- Flapan et al. (2006)
- Para obtener ejemplos adicionales de grafos intrínsecamente triple enlazados, véase Bowlin y Foisy (2004).
- Flapan et al. (2001)
- Como ya anunciaron anteriormente Robertson, Seymour y Thomas (1993b).
- La aplicación del algoritmo de Robertson-Seymour a este problema fue mencionada por Fellows y Langston (1988).
Referencias
- Böhme, Thomas (1990), «On spatial representations of graphs», en Bodendieck, Rainer, ed., Contemporary Methods in Graph Theory: In honor of Prof. Dr. Klaus Wagner, Mannheim: Bibliographisches Institut, Wissenschaftsverlag, pp. 151-167, ISBN 978-3-411-14301-6.. Citado por Robertson, Seymour y Thomas (1993a).
- Bothe, H.-G. (1973), «Problem P855», Colloquium Mathematicum 28: 163, New Scottish Book, Problem 876, 20.5.1972.. Citado por Sachs (1983).
- Bowlin, Garry; Foisy, Joel (2004), «Some new intrinsically 3-linked graphs», Journal of Knot Theory and its Ramifications 13 (8): 1021-1028, doi:10.1142/S0218216504003652..
- Conway, John H.; Gordon, Cameron McA. (1983), «Knots and links in spatial graphs», Journal of Graph Theory 7 (4): 445-453, doi:10.1002/jgt.3190070410..
- Fellows, Michael R.; Langston, Michael A. (1988), «Nonconstructive tools for proving polynomial-time decidability», Journal of the ACM 35 (3): 727-739, doi:10.1145/44483.44491..
- Flapan, Erica; Howards, Hugh; Lawrence, Don; Mellor, Blake (2006), «Intrinsic linking and knotting of graphs in arbitrary 3–manifolds», Algebraic & Geometric Topology 6: 1025-1035, arXiv:math/0508004, doi:10.2140/agt.2006.6.1025..
- Flapan, Erica; Naimi, Ramin; Pommersheim, James (2001), «Intrinsically triple linked complete graphs», Topology and its Applications 115 (2): 239-246, doi:10.1016/S0166-8641(00)00064-X..
- Flapan, Erica; Pommersheim, James; Foisy, Joel; Naimi, Ramin (2001), «Intrinsically n-linked graphs», Journal of Knot Theory and Its Ramifications 10 (8): 1143-1154, doi:10.1142/S0218216501001360..
- Fleming, Thomas; Diesl, Alexander (2005), «Intrinsically linked graphs and even linking number», Algebraic & Geometric Topology 5: 1419-1432, arXiv:math/0511133, doi:10.2140/agt.2005.5.1419..
- Foisy, Joel (2002), «Intrinsically knotted graphs», Journal of Graph Theory 39 (3): 178-187, doi:10.1002/jgt.10017..
- Foisy, Joel (2003), «A newly recognized intrinsically knotted graph», Journal of Graph Theory 43 (3): 199-209, doi:10.1002/jgt.10114..
- Hass, Joel; Lagarias, Jeffrey C.; Pippenger, Nicholas (1999), «The computational complexity of knot and link problems», Journal of the ACM 46 (2): 185-211, arXiv:math/9807016, doi:10.1145/301970.301971..
- van der Holst, Hein (2009), «A polynomial-time algorithm to find a linkless embedding of a graph», Journal of Combinatorial Theory, Series B 99 (2): 512-530, doi:10.1016/j.jctb.2008.10.002..
- Kawarabayashi, Ken-ichi; Kreutzer, Stephan; Mohar, Bojan (2010), «Linkless and flat embeddings in 3-space and the unknot problem», Proc. ACM Symposium on Computational Geometry (SoCG '10), pp. 97-106, doi:10.1145/1810959.1810975..
- Lovász, László; Schrijver, Alexander (1998), «A Borsuk theorem for antipodal links and a spectral characterization of linklessly embeddable graphs», Proceedings of the American Mathematical Society 126 (5): 1275-1285, doi:10.1090/S0002-9939-98-04244-0..
- Mader, W. (1968), «Homomorphiesätze für Graphen», Mathematische Annalen 178 (2): 154-168, doi:10.1007/BF01350657..
- Motwani, Rajeev; Raghunathan, Arvind; Saran, Huzur (1988), «Constructive results from graph minors: linkless embeddings», Proc. 29th IEEE Symposium on Foundations of Computer Science (FOCS '88), pp. 398-409, doi:10.1109/SFCS.1988.21956..
- Nešetřil, Jaroslav; Thomas, Robin (1985), «A note on spatial representation of graphs», Commentationes Mathematicae Universitatis Carolinae 26 (4): 655-659, archivado desde el original el 18 de julio de 2011..
- Robertson, Neil; Seymour, Paul (1995), «Graph Minors. XIII. The disjoint paths problem», Journal of Combinatorial Theory, Series B 63 (1): 65-110, doi:10.1006/jctb.1995.1006..
- Robertson, Neil; Seymour, Paul; Thomas, Robin (1993a), «A survey of linkless embeddings», en Robertson, Neil; Seymour, Paul, eds., Graph Structure Theory: Proc. AMS–IMS–SIAM Joint Summer Research Conference on Graph Minors, Contemporary Mathematics 147, American Mathematical Society, pp. 125-136..
- Robertson, Neil; Seymour, P. D.; Thomas, Robin (1993b), «Linkless embeddings of graphs in 3-space», Bulletin of the American Mathematical Society 28 (1): 84-89, MR 1164063, arXiv:math/9301216, doi:10.1090/S0273-0979-1993-00335-5..
- Robertson, Neil; Seymour, P. D.; Thomas, Robin (1995), «Sachs' linkless embedding conjecture», Journal of Combinatorial Theory, Series B 64 (2): 185-227, doi:10.1006/jctb.1995.1032..
- Robertson, Neil; Seymour, Paul; Thomas, Robin (1993c), «Hadwiger's conjecture for K6-free graphs», Combinatorica 13 (3): 279-361, doi:10.1007/BF01202354..
- Sachs, Horst (1983), «On a spatial analogue of Kuratowski's Theorem on planar graphs – an open problem», en Horowiecki, M.; Kennedy, J. W.; Sysło, M. M., eds., Graph Theory: Proceedings of a Conference held in Łagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics 1018, Springer-Verlag, pp. 230-241, doi:10.1007/BFb0071633..
- Saran, Huzur (1989), Constructive Results in Graph Minors: Linkless Embeddings, Ph.D. thesis, University of California, Berkeley..
- Truemper, Klaus (1992), Matroid Decomposition, Academic Press, pp. 100-101, archivado desde el original el 29 de agosto de 2017, consultado el 5 de septiembre de 2022..
Lecturas relacionadas
- Ramírez Alfonsín, J. L. (2005), «Knots and links in spatial graphs: a survey», Discrete Mathematics 302 (1–3): 225-242, doi:10.1016/j.disc.2004.07.035..