Grafo de ápice
En teoría de grafos, una rama de las matemáticas, un grafo de ápice (o también grafo apical o grafo de vértice) es un tipo de grafo que puede convertirse en un grafo plano mediante la eliminación de un solo vértice. El vértice eliminado se llama ápice del grafo. Es "un" ápice, y no "el" ápice, porque uno de estos grafos puede tener más de uno, como por ejemplo en el caso de los grafos mínimos no planos K5 o K3,3, en los que cada vértice es un ápice. Los grafos de ápice incluyen grafos que en sí mismos son planos, en cuyo caso nuevamente cada vértice es un ápice. El grafo nulo también se cuenta como un grafo de ápice aunque no tenga ningún vértice para eliminar.
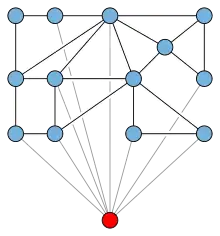
Son cerrados bajo la operación de tomar menores y juegan un papel considerable en varios otros aspectos de la teoría de grafos menores: los embebidos sin enlaces,[1] la conjetura de Hadwiger,[2] los grafos YΔY-reducibles,[3] y su relación con el ancho de árbol y con el diámetro de un grafo.[4]
Caracterización e identificación
Los grafos de ápice son cerrados bajo la operación de tomar menores: contraer cualquier arista, o eliminar cualquier arista o vértice, conduce a otro grafo apical. Porque, si G es un grafo de vértice con ápice v, entonces cualquier contracción o eliminación que no involucre a v conserva la planitud del grafo restante, al igual que cualquier eliminación de una arista que incida en v. Si se contrae una arista incidente en v, el efecto sobre el grafo restante es equivalente a la eliminación del otro extremo de la arista. Y si se elimina v, se puede elegir cualquier otro vértice como ápice.[5]
Por el teorema de Robertson-Seymour, debido a que forman una familia de grafos cerrados menores, los grafos de ápice tienen una caracterización de grafo prohibido. Solo hay un número finito de grafos que no son grafos de ápice ni tienen otro grafo que no sea de ápice como menor. Estos grafos son menores prohibidos por la propiedad de ser un grafo de ápice.
Cualquier otro grafo G es un grafo de ápice si y solo si ninguno de los menores prohibidos es un menor de G. Estos menores prohibidos incluyen los siete grafos de la familia de Petersen, tres grafos desconectados formados a partir de las uniones disjuntas de K5 y K3,3, y muchos otros grafos. Sin embargo, se desconoce una descripción completa de ellos.[5](Pierce, 2014)
A pesar de que se desconoce el conjunto completo de menores prohibidos, es posible probar si un grafo dado es un grafo de vértice y, de ser así, encontrar un vértice para el grafo mediante un algoritmo de complejidad temporal. De manera más general, para cualquier k constante fija, es posible reconocer en tiempo lineal los grafos k-apicales, los grafos en los que la eliminación de un conjunto cuidadosamente elegido de como máximo k vértices conduce a un grafo plano.[6] Sin embargo, si k es variable, el problema es NP-completo.[7]
Número cromático
Cada grafo de ápice tiene número cromático como máximo de cinco: el grafo plano subyacente requiere como máximo cuatro colores por el teorema de los cuatro colores, y el ápice restante necesita como máximo un color adicional.Robertson, Seymour y Thomas (1993a) usó este hecho en su prueba del caso k= 6 de la conjetura de Hadwiger, la afirmación de que cada grafo 6-cromático tiene el grafo completo K6 como menor: demostraron que cualquier contraejemplo mínimo a la conjetura tendría que ser un grafo de ápice, pero dado que no hay grafos de ápice 6-cromáticos, no puede existir un contraejemplo.
Jørgensen (1994) conjeturó que todo grafo 6-vértices-conectado que no tenga K6 como menor debe ser un grafo de ápice. Si esto se probara, el resultado de Robertson-Seymour-Thomas sobre la conjetura de Hadwiger sería una consecuencia inmediata.[2] La conjetura de Jørgensen sigue sin probarse.[8] Sin embargo, si es falsa, solo tiene un número finito de contraejemplos.(Kawarabayashi et al., 2012)
Ancho de árbol local
Una familia de grafos F tiene ancho de árbol local acotado si los grafos en F obedecen a una relación funcional entre el diámetro y el ancho de árbol: existe una función f tal que el ancho de árbol de un grafo de diámetro-d en F es como máximo f (d). Los grafos de ápice no tienen un ancho de árbol local acotado: los grafos de ápice formados al conectar un ápice a cada vértice de un grafo de celosía de n × n tienen un ancho de árbol n y un diámetro de 2, por lo que el ancho de árbol no está limitado por una función de diámetro para estos grafos. Sin embargo, los grafos de vértice están íntimamente conectados con el ancho de árbol local acotado: las familias de grafos cerrados menores F que tienen un ancho de árbol local acotado son exactamente las familias que tienen un grafo de ápice como uno de sus menores prohibidos.[4] Una familia de grafos cerrados de menor importancia que tiene un grafo de ápice como uno de sus menores prohibidos se conoce como libre de menores de ápice. Con esta terminología, la conexión entre los grafos de ápice y el ancho de árbol local se puede reafirmar como el hecho de que las familias de grafos libres menores de ápice son las mismas que las familias de grafos cerrados menores con ancho de árbol local acotado.
El concepto de ancho de árbol local acotado forma la base de la teoría de bidimensionalidad y permite que muchos problemas algorítmicos en grafos libres de menores de ápice se resuelvan exactamente mediante un algoritmo de tiempo polinomial o un algoritmo manejable de parámetros fijos, o se aproximen usando un esquema de aproximación de tiempo polinomial.[9] Las familias de grafos sin menores de ápice obedecen a una versión reforzada del teorema de estructura de grafos, lo que lleva a algoritmos de aproximación adicionales para la coloración de grafos y para el problema del viajante.[10] Sin embargo, algunos de estos resultados también se pueden extender a familias de grafos cerrados menores arbitrarios a través de teoremas de estructura que los relacionan con grafos libres de menores de ápice.[11]
Incrustaciones
Si G es un grafo de ápice con v como ápice, y τ es el número mínimo de caras necesarias para cubrir todos los vecinos de v en una incrustación plana de G \ {v},, entonces G puede estar incrustado en una superficie bidimensional de genus τ – 1. Para comprobarlo, simplemente basta agregar el número de puentes al empotramiento plano, conectando entre sí todas las caras en las que se debe enlazar v. Por ejemplo, al agregar un solo vértice a un grafo plano exterior (un grafo con τ= 1) se produce un grafo plano. Cuando G \ {v} es 3-conectado, su límite está dentro de un factor constante de óptimo: cada incrustación superficial de G requiere género al menos τ160. Sin embargo, es de complejidad NP determinar el género óptimo de una superficie incrustada de un grafo de ápice.[12]
Al usar árboles SPQR para codificar las posibles incrustaciones de la parte plana de un grafo de ápice, es posible obtener un dibujo del grafo en el plano en el que los únicos cruces involucran al ápice, minimizando el número total de cruces, en tiempo polinómico.[13] Sin embargo, si se permiten cruces arbitrarios, se vuelve de complejidad NP minimizar el número de cruces, incluso en el caso especial de los grafos de vértice formados al agregar una sola arista a un grafo plano.[14]
Los grafos de vértice también son embebibles sin enlaces en el espacio tridimensional: se pueden incrustar de tal manera que cada ciclo del grafo sea el límite de un disco que no está atravesado por ningún otro elemento del grafo.[15] Un dibujo de este tipo puede obtenerse representando la parte plana del grafo en un plano, colocando el ápice sobre el plano y conectándolo mediante aristas en línea recta a cada uno de sus vecinos. Los grafos incrustables sin enlaces forman una familia cerrada de menores con los siete grafos de la familia de Petersen como sus menores mínimos prohibidos; por lo tanto,[1] estos grafos también están prohibidos como menores para los grafos de ápice. Sin embargo, existen grafos integrables sin enlaces que no son grafos de ápice.
YΔY-reducibilidad
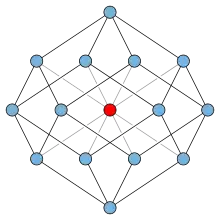
Un grafo conexo es YΔY-reducible si puede reducirse a un solo vértice mediante una secuencia de pasos, cada uno de los cuales es una transformación Δ-Y o Y-Δ, la eliminación de un autobucle o de una adyacencia múltiple, la eliminación de un vértice con un vecino, y la sustitución de un vértice de grado dos y sus dos aristas vecinas por una sola arista.[3]
Al igual que los grafos de vértice y los grafos embebibles sin enlaces, los grafos reducibles YΔY están cerrados bajo grafos menores. Y, al igual que los grafos embebibles sin enlaces, los grafos reducibles YΔY tienen los siete grafos de la familia de Petersen como menores prohibidos, lo que genera la pregunta de si estos son los únicos menores prohibidos y si los grafos reducibles YΔY son los mismos que los grafos embebibles sin enlaces. Sin embargo, Neil Robertson proporcionó un ejemplo de un grafo de ápice que no es reducible mediante la transformación YΔY. Dado que cada grafo de ápice se puede incorporar sin enlaces, esto muestra que hay grafos que se pueden incorporar sin enlaces pero no reducibles con YΔY y, por lo tanto, hay menores prohibidos adicionales para los grafos reducibles con YΔY.[3]
El grafo de vértice de Robertson se muestra en la figura. Se puede obtener conectando el ápice a cada uno de los vértices de grado tres de un rombododecaedro, o fusionando dos vértices diametralmente opuestos del grafo de un hipercubo de cuatro dimensiones. Debido a que el grafo del dodecaedro rómbico es plano, el grafo de Robertson es un grafo de ápice. También es un grafos sin triángulos con un menor de grado cuatro, por lo que no se puede cambiar por ninguna reducción de YΔY.[3]
Grafos casi planos
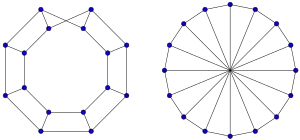
Si un grafo es un grafo de ápice, no es necesariamente el caso de que tenga un vértice único. Por ejemplo, en los grafos no planos de menor-mínimo K5 y K3,3, cualquiera de los vértices se puede elegir como vértice.Wagner (1970) definió un grafo casi plano como un grafo de ápice no plano con la propiedad de que todos los vértices pueden ser ápices del grafo; por lo tanto, K5 y K3,3 son casi planos. Proporcionó una clasificación de estos grafos en cuatro subconjuntos, uno de los cuales consta de los grafos que (como la escalera de Möbius) se pueden incrustar en la banda de Möbius de tal manera que el borde único de la tira coincida con un camino hamiltoniano del grafo. Antes de la prueba del teorema de los cuatro colores, se demostró que cada grafo casi plano se puede colorear con un máximo de cuatro colores, a excepción de los grafos formados a partir de un grafo rueda con un ciclo externo impar al reemplazar el vértice central con dos vértices adyacentes, lo que requiere cinco colores. Además, demostró que, con una sola excepción (el grafo complemento de ocho vértices del cubo), cada grafo casi plano tiene una incrustación en el plano proyectivo.
Sin embargo, la expresión grafo casi plano es muy ambigua: también se ha utilizado para referirse a grafos de ápice, grafos[16] formados al agregar una arista a un grafo plano,[17] y grafos formados a partir de un grafo incrustado plano al reemplazar un número acotado de caras por vórtices de ancho de ruta acotado,[18] así como para otros conjuntos de grafos definidos con menos precisión.
Clases de grafos relacionados
Se dice que un grafo abstracto es de n-ápices si se puede hacer plano eliminando n o menos vértices. Un grafo de 1 vértice también se dice que es de ápice.
De acuerdo con Lipton et al. (2018), un grafo se denomina de arista-ápice si hay una arista que se puede eliminar para hacer que sea plano. Análogamente, se dice que un grafo es de ápice por contracción si hay alguna arista que se puede contraer para hacer que sea plano.
Véase también
- Pirámide poliédrica, un politopo de 4 dimensiones cuyos vértices y aristas forman un grafo de ápice, con el ápice adyacente a cada vértice de un grafo poliédrico
Referencias
- Robertson, Seymour y Thomas (1993b).
- Robertson, Seymour y Thomas (1993a).
- Truemper (1992).
- Eppstein (2000);Demaine y Hajiaghayi (2004).
- Gupta y Impagliazzo (1991).
- Kawarabayashi (2009).
- Lewis y Yannakakis (1980).
- «Jorgensen's Conjecture», Open Problem Garden, consultado el 13 de noviembre de 2016..
- Eppstein (2000);Frick y Grohe (2001);Demaine y Hajiaghayi (2005).
- Demaine, Hajiaghayi y Kawarabayashi (2009).
- Grohe (2003).
- Mohar (2001).
- Chimani et al. (2009).
- Cabello y Mohar (2010).
- Robertson, Seymour y Thomas (1993c).
- Robertson, Seymour y Thomas (1993c);Eppstein (2000).
- Archdeacon y Bonnington (2004).
- Abraham y Gavoille (2006).
Bibliografía
- Abraham, Ittai; Gavoille, Cyril (2006), «Object location using path separators», Proc. 25th ACM Symposium on Principles of Distributed Computing (PODC '06), pp. 188-197, doi:10.1145/1146381.1146411..
- Archdeacon, Dan; Bonnington, C.P.C. Paul (2004), «Obstructions for embedding cubic graphs on the spindle surface», Journal of Combinatorial Theory, Series B 91 (2): 229-252, doi:10.1016/j.jctb.2004.02.001..
- Cabello, Sergio; Mohar, Bojan (2010), «Adding one edge to planar graphs makes crossing number hard», Proc. 26th ACM Symposium on Computational Geometry (SoCG '10), pp. 68-76, doi:10.1145/1810959.1810972, archivado desde el original el 14 de marzo de 2012, consultado el 2 de agosto de 2010..
- Chimani, Markus; Gutwenger, Carsten; Mutzel, Petra; Wolf, Christian (2009), «Inserting a vertex into a planar graph», Proc. 20th ACM-SIAM Symposium on Discrete Algorithms (SODA '09), pp. 375-383..
- Demaine, Erik D.; Hajiaghayi, Mohammad Taghi (2004), «Diameter and treewidth in minor-closed graph families, revisited», Algorithmica 40 (3): 211-215, doi:10.1007/s00453-004-1106-1..
- Demaine, Erik D.; Hajiaghayi, Mohammad Taghi (2005), «Bidimensionality: new connections between FPT algorithms and PTASs», Proc. 16th ACM-SIAM Symposium on Discrete Algorithms (SODA '05), pp. 590-601, archivado desde el original el 11 de diciembre de 2018, consultado el 2 de agosto de 2010..
- Demaine, Erik D.; Hajiaghayi, Mohammad Taghi; Kawarabayashi, Ken-ichi (2009), «Approximation algorithms via structural results for apex-minor-free graphs», Proc. 36th International Colloquium Automata, Languages and Programming (ICALP '09), Lecture Notes in Computer Science 5555, Springer-Verlag, pp. 316-327, doi:10.1007/978-3-642-02927-1_27..
- Eppstein, David (2000), «Diameter and treewidth in minor-closed graph families», Algorithmica 27 (3): 275-291, arXiv:math.CO/9907126, doi:10.1007/s004530010020..
- Frick, Markus; Grohe, Martin (2001), «Deciding first-order properties of locally tree-decomposable structures», Journal of the ACM 48 (6): 1184-1206, arXiv:cs/0004007, doi:10.1145/504794.504798..
- Grohe, Martin (2003), «Local tree-width, excluded minors, and approximation algorithms», Combinatorica 23 (4): 613-632, arXiv:math.CO/0001128, doi:10.1007/s00493-003-0037-9..
- Gupta, A.; Impagliazzo, R. (1991), «Computing planar intertwines», Proc. 32nd IEEE Symposium on Foundations of Computer Science (FOCS '91), IEEE Computer Society, pp. 802-811, doi:10.1109/SFCS.1991.185452..
- Jørgensen, Leif K. (1994), «Contractions to K8», Journal of Graph Theory 18 (5): 431-448, doi:10.1002/jgt.3190180502.. Citado por Plantilla:Harvs.
- Kawarabayashi, Ken-ichi (2009), «Planarity allowing few error vertices in linear time», Proc. 50th IEEE Symposium on Foundations of Computer Science (FOCS '09), IEEE Computer Society, pp. 639-648, doi:10.1109/FOCS.2009.45..
- Kawarabayashi, Ken-ichi; Norine, Serguei; Thomas, Robin; Wollan, Paul (2012), minors in large 6-connected graphs, Bibcode:2012arXiv1203.2192K, arXiv:1203.2192..
- Lewis, John M.; Yannakakis, Mihalis (1980), «The node-deletion problem for hereditary properties is NP-complete», Journal of Computer and System Sciences 20 (2): 219-230, doi:10.1016/0022-0000(80)90060-4..
- Lipton, Max; Mackall, Eoin; Mattman, Thomas W.; Pierce, Mike; Robinson, Samantha; Thomas, Jeremy; Weinschelbaum, Ilan (2018), «Six variations on a theme: Almost planar graphs», Involve, A Journal of Mathematics 11 (3): 413-448, arXiv:1608.01973, doi:10.2140/involve.2018.11.413..
- Mohar, Bojan (2001), «Face covers and the genus problem for apex graphs», Journal of Combinatorial Theory, Series B 82 (1): 102-117, doi:10.1006/jctb.2000.2026, archivado desde el original el 22 de septiembre de 2017, consultado el 2 de agosto de 2010..
- Pierce, Mike (2014), Searching for and classifying the finite set of minor-minimal non-apex graphs, Honours thesis, California State University, Chico..
- Robertson, Neil; Seymour, Paul; Thomas, Robin (1993a), «Hadwiger's conjecture for K6-free graphs», Combinatorica 13 (3): 279-361, doi:10.1007/BF01202354..
- Robertson, Neil; Seymour, P. D.; Thomas, Robin (1993b), «Linkless embeddings of graphs in 3-space», Bulletin of the American Mathematical Society 28 (1): 84-89, MR 1164063, arXiv:math/9301216, doi:10.1090/S0273-0979-1993-00335-5..
- Robertson, Neil; Seymour, Paul; Thomas, Robin (1993c), «A survey of linkless embeddings», en Robertson, Neil; Seymour, Paul, eds., Graph Structure Theory: Proc. AMS–IMS–SIAM Joint Summer Research Conference on Graph Minors, Contemporary Mathematics 147, American Mathematical Society, pp. 125-136..
- Truemper, Klaus (1992), Matroid Decomposition, Academic Press, pp. 100-101, archivado desde el original el 29 de agosto de 2017, consultado el 14 de septiembre de 2022..
- Wagner, Klaus (1967), «Fastplättbare Graphen», Journal of Combinatorial Theory (en alemán) 3 (4): 326-365, doi:10.1016/S0021-9800(67)80103-0..
- Wagner, Klaus (1970), «Zum basisproblem der nicht in die projektive ebene einbettbaren graphen, I», Journal of Combinatorial Theory (en alemán) 9 (1): 27-43, doi:10.1016/S0021-9800(70)80052-7..