Movimiento de lazo
El movimiento de lazo es una autooscilación, generalmente no deseada, que se genera alrededor de un punto de equilibrio mecánico.[1] La expresión inglesa ("hunting oscillation") empezó a usarse en el siglo XIX, y hace referencia a cómo un sistema "persigue" alcanzar un punto de equilibrio. La expresión se utiliza para describir fenómenos en campos tan diversos como la electrónica, la aviación, la biología y la ingeniería ferroviaria.
Ruedas de ferrocarril
Un movimiento de lazo clásico es el balanceo de un vehículo ferroviario causado por la acción de la conicidad de la que depende la estabilidad direccional de un ferrocarril. Surge de la interacción de las fuerzas de adherencia y de las fuerzas de inercia. A baja velocidad, el efecto de la adherencia es dominante, pero a medida que aumenta la velocidad, las fuerzas de adherencia y las fuerzas de inercia se vuelven comparables en magnitud y la oscilación comienza a hacerse presente a partir de una velocidad crítica. Por encima de esta velocidad, el movimiento puede ser violento, dañar la vía y las ruedas, y potencialmente puede causar un descarrilamiento. El problema (vinculado a que las dos ruedas de un eje rígido giran con la misma velocidad angular) no se produce en los sistemas dotados con un diferencial (solución bastante inusual en la práctica), y los trenes convencionales tienen sus ruedas fijas a los ejes de dos en dos. Algunos trenes, como el Talgo 350, no tienen un diferencial, pero no se ven afectados por la oscilación, que sus ruedas giran independientemente unas de las otras. Sin embargo, los coches de viajeros convencionales pueden verse afectados, porque las ruedas de sus bogíes se fijan a los ejes en parejas. Los bogíes con menor conicidad, y equipados con ruedas que giran independientemente entre sí (no fijadas a un eje rígido en parejas), son más baratos que un diferencial adecuado para el mismo bogíe.[2]
El problema se notó por primera vez hacia fines del siglo XIX, cuando las velocidades de los trenes se volvieron lo suficientemente altas como para empezar a hacerlo patente. Los primeros esfuerzos serios para contrarrestarlo se pusieron en marcha en la década de 1930, dando lugar a diseños con grandes distancias entre ejes y a la suspensión oscilante de amortiguación lateral. En el desarrollo del Shinkansen japonés, se usaron ruedas con menor conicidad y se introdujeron otros cambios de diseño para extender las velocidades de circulación por encima de los 225 km/h. Los avances en el diseño de las ruedas basados en los esfuerzos de investigación y desarrollo en Europa y Japón han extendido las velocidades de los sistemas de ruedas de acero mucho más allá de las alcanzadas por el Shinkansen original, mientras que la ventaja de la compatibilidad con las vías clásicas mantiene el predominio de dicha tecnología sobre alternativas como el Hovertrén y los sistemas maglev. El TGV francés tiene el récord de velocidad de los trenes con ruedas de acero, con un registro de 574,9 kilómetros por hora (357 mph).
Análisis cinemático
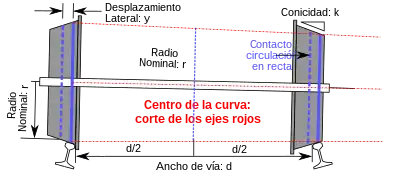
Mientras que una descripción cualitativa proporciona cierta comprensión del fenómeno, una comprensión más profunda inevitablemente requiere un análisis matemático de la dinámica del vehículo. Incluso entonces, los resultados pueden ser solo aproximados.
Una descripción cinemática trata de la geometría del movimiento, sin referencia a las fuerzas que lo causan, por lo que el análisis comienza con una descripción de la geometría de una pareja de ruedas ligadas a un eje rígidamente que se desplaza sobre un tramo de vía en recta. Como la Segunda Ley de Newton relaciona las fuerzas con las aceleraciones de los cuerpos, las fuerzas que actúan pueden derivarse de la cinemática calculando las aceleraciones de los componentes. Sin embargo, si estas fuerzas cambian la descripción cinemática (como lo hacen en este caso), entonces los resultados solo pueden ser aproximadamente correctos.
Suposiciones y descripciones no matemáticas
Esta descripción cinemática hace una serie de suposiciones simplificadoras, ya que ignora las fuerzas. Por un lado, se supone que la resistencia a la rodadura es cero. Un juego de ruedas (no conectado a un tren o bogíe) se empuja hacia adelante en una vía recta y nivelada. El juego de ruedas comienza a moverse por inercia y nunca se desacelera, ya que no hay fuerzas (excepto las fuerzas hacia abajo sobre el juego de ruedas para que se adhiera a la pista y no deslice). Si inicialmente el juego de ruedas se centra en la vía del ferrocarril, entonces los diámetros efectivos de cada rueda son los mismos y el juego de ruedas rueda por la pista en una línea perfectamente recta para siempre. Pero si el juego de ruedas está un poco descentrado, de modo que los diámetros efectivos (o radios) son diferentes, entonces el juego de ruedas comienza a moverse en una curva de radio R (dependiendo de los radios del juego de ruedas, que se describen más adelante) . El problema es utilizar el razonamiento cinemático para encontrar la trayectoria del juego de ruedas, o más precisamente, la trayectoria del centro del juego de ruedas proyectado verticalmente sobre la plataforma con respecto al centro de la vía. Se trata de una trayectoria sobre un plano horizontal paralelo a la superficie de la tierra, representada en un gráfico xy, donde x es la distancia a lo largo de la vía del ferrocarril, e y es el "error de seguimiento", la desviación del centro del juego de ruedas medido desde la línea recta que pasa por el centro de la vía (a medio camino entre los dos raíles).
Para ilustrar que un juego de ruedas sigue una trayectoria curva, se puede colocar un clavo o tornillo en una mesa plana y darle un pequeño impulso. Rodará describiendo un círculo, porque es como un juego de ruedas de diámetro extremadamente diferente. La cabeza es análoga a una rueda de gran diámetro y el extremo puntiagudo es como una rueda de pequeño diámetro. Si bien el clavo o el tornillo girarán en un círculo completo (o incluso más), el juego de ruedas del ferrocarril se comporta de manera diferente porque tan pronto como comienza a girar en una curva, los diámetros efectivos cambian de tal manera que disminuyen la curvatura de la ruta. Téngase en cuenta que "radio" y "curvatura" se refieren a la curvatura de la trayectoria del juego de ruedas y no a la curvatura del ferrocarril, ya que esta es una vía perfectamente recta. A medida que avanza el juego de ruedas, la curvatura disminuye hasta que las ruedas alcanzan el punto donde sus diámetros efectivos son iguales y el camino ya no se curva. Pero la trayectoria tiene una pendiente en este punto (es una línea recta que cruza diagonalmente sobre la línea central de la vía) de modo que sobrepasa la línea central y los diámetros efectivos se invierten (la rueda de menor diámetro anterior se convierte en el diámetro más grande y al revés). Esto da como resultado que el juego de ruedas se mueva en una curva en la dirección opuesta. Nuevamente sobrepasa la línea central y este fenómeno continúa indefinidamente con el juego de ruedas oscilando de lado a lado. Debe tenerse en cuenta que la pestaña de la rueda nunca hace contacto con el riel. En este modelo, se supone que los rieles siempre permanecen en contacto con la banda de rodadura de la rueda a lo largo de la misma línea en la cabeza del riel, lo que implica que a efectos de cálculo, los raíles es como si estuvieran afilados y solo hicieran contacto con la banda de rodadura de la rueda a lo largo de una recta (de ancho cero).
Análisis matemático
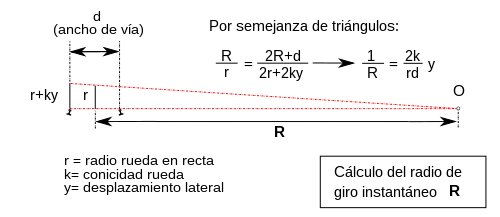
El tren permanece en la vía en virtud de la forma cónica de las huellas de las ruedas. Si un juego de ruedas se desplaza hacia un lado en una cantidad "y" (coincidente con el error de desviación respecto al eje rectilíneo de la vía), el radio de la banda de rodadura en contacto con el raíl en un lado se reduce, mientras que en el otro lado se incrementa. La velocidad angular es la misma para ambas ruedas (dado que están acopladas a través de un eje rígido), por lo que la banda de rodadura de mayor diámetro se acelera, mientras que la más pequeña se desacelera. El juego de ruedas gira alrededor de un centro de curvatura definido por la intersección de la generatriz de un cono que pasa a través de los puntos de contacto fe las ruedas con los raíles y el eje del juego de ruedas. Aplicando triángulos semejantes, se tiene que para el radio de giro:
donde d es el ancho de vía, r el radio de la rueda cuando se circula en línea recta, y k es la inclinación de la banda de rodadura (que es la conicidad de la rueda).
La trayectoria del juego de ruedas en relación con la vía recta está definida por una función y(x), donde x representa el avance a lo largo de la vía. Este desplazamiento transversal a veces se denomina error de seguimiento.[3] Siempre que la dirección del movimiento permanezca más o menos paralela a los raíles, la curvatura de la trayectoria puede estar relacionada aproximadamente con la segunda derivada de y con respecto a la distancia a lo largo de la vía.[4]
De ello se deduce que la trayectoria a lo largo de la vía se rige por la ecuación:[5]
Este es un movimiento armónico simple, que tiene longitud de onda:
- conocida como la fórmula de Klingel (deducida en 1883)[6]
Este análisis cinemático implica que los trenes se balancean de lado a lado todo el tiempo. De hecho, esta oscilación se amortigua por debajo de una velocidad crítica y, por lo tanto, el viaje es más cómodo. El resultado cinemático ignora las fuerzas que causan el movimiento. Estos pueden analizarse utilizando el concepto de fluencia (no lineal), pero son algo difíciles de cuantificar simplemente, ya que surgen de la distorsión elástica de la rueda y el raíl en las regiones de contacto, fenómeno del que se ocupa la mecánica de contacto por fricción; Carter presentó una primera interpretación que incluye estos efectos en el análisis del movimiento de lazo.[7] Véase Knothe[8] para un relato histórico.
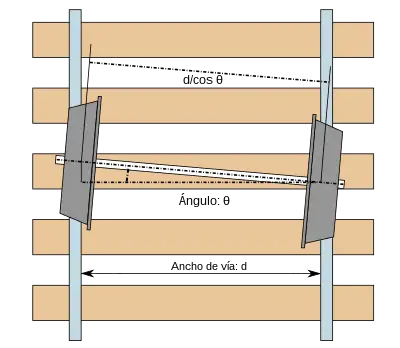
Si el movimiento es sustancialmente paralelo a la posición de los raíles, el desplazamiento angular del conjunto de las dos ruedas viene dado por:
De ahí:
La desviación angular también sigue un movimiento armónico simple, que subyace por detrás del movimiento de lado a lado en un cuarto de ciclo. En muchos sistemas que se caracterizan por un movimiento armónico que involucra dos estados diferentes (en este caso, la desviación de guiñada del eje y el desplazamiento lateral), el retraso de un cuarto de ciclo entre los dos movimientos dota al sistema de la capacidad de extraer energía del movimiento hacia adelante. Este efecto se observa en el "aleteo" de las alas de los aviones o en el "tambaleo" de los vehículos de carretera, así como el movimiento de lazo en los vehículos ferroviarios. La solución cinemática deducida anteriormente describe el movimiento a la velocidad crítica.
En la práctica, por debajo de la velocidad crítica, el desfase entre los dos movimientos es inferior a un cuarto de ciclo, de modo que el movimiento se amortigua, pero, por encima de la velocidad crítica, el desfase es superior a un cuarto de ciclo, de modo que el movimiento se amplifica.
Para estimar las fuerzas de inercia, es necesario expresar las derivadas de distancia como derivadas respecto al tiempo. Esto se hace usando la velocidad del vehículo U, que se supone constante:
La aceleración angular del eje en guiñada es:
El momento de inercia (ignorando los efectos giroscópicos) es:
donde F es la fuerza que actúa a lo largo de los rieles y C es el momento de inercia del juego de ruedas.
La fuerza de fricción máxima entre la rueda y el raíl viene dada por:
donde W es la carga por eje y es el coeficiente de fricción. El deslizamiento brusco se producirá con una combinación de velocidad y desviación del eje dada por:
Esta expresión produce una sobreestimación significativa de la velocidad crítica, pero ilustra la razón física por la que ocurre el movimiento de lazo, es decir, las fuerzas de inercia se vuelven comparables con las fuerzas de adherencia por encima de una velocidad determinada. Limitar la fricción es una representación pobre de la fuerza de adherencia en este caso.
Las fuerzas de adherencia reales surgen de la distorsión de la banda de rodadura y el raíl en la región de contacto. No se producen grandes deslizamientos, sino solo distorsión elástica y algo de deslizamiento local (deslizamiento de arrastre). Durante el funcionamiento normal, estas fuerzas están dentro de la limitación de la restricción de fricción. Un análisis completo tiene en cuenta estas fuerzas, utilizando teorías de la mecánica de contacto rodante.
Sin embargo, cuando se realizó el análisis cinemático se supuso que no había ningún deslizamiento en el contacto entre el raíl y la rueda. Ahora está claro que hay un deslizamiento debido a la fluencia que hace que la trayectoria sinusoidal calculada del juego de ruedas (según la fórmula de Klingel) no sea exactamente correcta.
Balance de energía
Para obtener una estimación de la velocidad crítica, se aprovecha el hecho de que la condición para la que esta solución cinemática es válida corresponde al caso en el que no hay intercambio neto de energía con el entorno. Por lo tanto, considerando la energía cinética y potencial del sistema, se debería poder deducir la velocidad crítica.
Sea:
Usando el operador:
la ecuación de la aceleración angular se puede expresar en términos de la velocidad angular de guiñada:
integrando:
entonces la energía cinética debido a la rotación es:
Cuando el eje se desvía, los puntos de contacto se mueven hacia afuera en las bandas de rodadura, de modo que se baja la altura del eje. La distancia entre los puntos de soporte aumenta a:
para pequeñas cantidades de segundo orden, el desplazamiento del punto de apoyo desde los centros de las huellas es:
la carga por eje varía según
El trabajo realizado al bajar la carga por eje es, por lo tanto:
Esta es la energía perdida del sistema, por lo que para que el movimiento continúe, se debe extraer una cantidad igual de energía del movimiento hacia adelante del juego de ruedas.
La velocidad de la rueda exterior viene dada por:
La energía cinética es:
para la rueda interior es
donde m es la masa de ambas ruedas.
El aumento de la energía cinética es:
El movimiento continuará a una amplitud constante siempre que la energía extraída del movimiento hacia adelante, y que se manifieste como una mayor energía cinética de la rueda puesta a cero guiñada, sea igual a la energía potencial perdida por la disminución de la carga del eje a la guiñada máxima.
Ahora, desde el punto de vista cinemático:
pero
La energía cinética traslacional es
La energía cinética total es:
La velocidad crítica se encuentra en el balance de energía:
Por lo tanto, la velocidad crítica viene dada por
Esto es independiente de la forma cónica de la rueda, pero depende de la relación entre la carga del eje y la masa del juego de ruedas. Si las bandas de rodadura fueran verdaderamente cónicas, la velocidad crítica sería independiente de la conicidad. En la práctica, el desgaste de la rueda hace que el cono varíe a lo ancho de la banda de rodadura, de modo que el valor del cono utilizado para determinar la energía potencial es diferente del utilizado para calcular la energía cinética. Denotando el primero como a, la velocidad crítica se convierte en:
donde a es ahora un factor de forma determinado por el desgaste de la rueda. Este resultado se deduce[9] de un análisis de la dinámica del sistema utilizando métodos de ingeniería de control estándar.
Limitaciones del análisis simplificado
El movimiento de un juego de ruedas es mucho más complicado de lo que indicaría este análisis. La suspensión del vehículo aplica fuerzas de restricción adicionales[10] y, a alta velocidad, el juego de ruedas generará pares giroscópicos adicionales, que modificarán la estimación de la velocidad crítica. Convencionalmente, un vehículo ferroviario tiene movimiento estable a bajas velocidades. Cuando alcanza altas velocidades, la estabilidad cambia a una forma inestable. El objetivo principal del análisis no lineal de la dinámica del sistema de vehículos ferroviarios es mostrar la visión de la investigación analítica del compromiso entre la estabilidad lateral no lineal y el comportamiento de movimiento de lazo de los vehículos ferroviarios en una vía tangente. Este estudio contiene el método de Bogoliubov para su análisis.[11]
Dos cuestiones principales, es decir, asumir la carrocería del vehículo como un soporte fijo, y la influencia de los elementos no lineales en el cálculo de la velocidad crítica del movimiento de lazo, se asumen en la mayoría de los estudios.[12] Un vehículo ferroviario real tiene muchos más grados de libertad y, en consecuencia, puede tener más de una velocidad crítica; de ninguna manera es seguro que la más baja esté condicionada por el movimiento del juego de ruedas.
Sin embargo, el análisis es instructivo porque muestra por qué ocurre el movimiento de lazo. A medida que aumenta la velocidad, las fuerzas de inercia se vuelven comparables con las fuerzas de adherencia. Es por eso que la velocidad crítica depende de la relación entre la carga del eje (que determina la fuerza de adherencia) y la masa del juego de ruedas (que determina las fuerzas de inercia).
Alternativamente, por debajo de cierta velocidad, la energía que se extrae del movimiento hacia adelante es insuficiente para reemplazar la energía perdida al bajar los ejes, y el movimiento se amortigua; Por encima de esta velocidad, la energía extraída es mayor que la pérdida de energía potencial y la amplitud se acumula.
La energía potencial en la guiñada máxima del eje puede incrementarse incluyendo una restricción elástica sobre el movimiento de guiñada del eje, de modo que haya una contribución que surja de la tensión de un muelle. La disposición de ruedas en bogíes para aumentar la restricción sobre el movimiento de guiñada de los juegos de ruedas y la aplicación de restricciones elásticas al bogíe también aumenta la velocidad crítica. La introducción de fuerzas elásticas en la ecuación permite diseños de suspensión que están limitados solo por el inicio del deslizamiento bruto, en lugar de por rl movimiento de lazo clásico. La penalización que debe pagarse por la eliminación virtual del movimiento de lazo es la adopción de un trazado de las vías más rectilíneo, con el problema asociado de las expropiaciones necesarias y la incompatibilidad con las infraestructuras tradicionales existentes.
El movimiento de lazo es un problema dinámico que puede resolverse, al menos en principio, mediante un control de retroalimentación activo, que puede adaptarse a la calidad de la vía. Sin embargo, la introducción del control activo plantea problemas de fiabilidad y seguridad.
Poco después del inicio del movimiento de lazo, se produce un gran deslizamiento y las pestañas de las ruedas impactan en los carriles, lo que puede causar daños en ambos.
Vehículos de carretera y ferrocarril

Muchos vehículos de carretera-ferrocarril tienen ejes independientes y sistemas de suspensión en cada rueda ferroviaria. Cuando este diseño se combina con el uso simultáneo de neumáticos sobre el raíl, se hace difícil usar las fórmulas anteriores. Históricamente, los vehículos de carretera y ferrocarril tienen sus ruedas delanteras ligeramente convergentes, lo que se ha demostrado que minimiza el movimiento de lazo mientras el vehículo circula por las vías del tren.
Véase también
- Mecánica de contacto por fricción
- Adherencia rueda-carril
- Perfil del raíl
- Velocidad de tambaleo
- Dinámica de vehículos
- Juego de ruedas
Para conocer los métodos generales relacionados con esta clase de problema, véase
Referencias
- Oxford English Dictionary (2nd edición). Oxford University Press. 1989. «f. The action of a machine, instrument, system, etc., that is hunting (see hunt v. 7b); an undesirable oscillation about an equilibrium speed, position, or state. (La acción de una máquina, instrumento, sistema, etc., que está oscilando (ver oscilar v. 7b); una oscilación indeseable sobre una velocidad, posición o estado de equilibrio.) ».
- Talgo 350
- El "error de seguimiento" será cero si la trayectoria de las ruedas corre absolutamente recta a lo largo de la vía, y el par de ruedas está centrado en la vía.
- Véase curvatura para obtener detalles matemáticos. La igualdad aproximada se convierte en igualdad solo cuando el error de seguimiento "y", tiene pendiente cero con respecto a "x". Dado que el error de seguimiento resultará ser una onda sinusoidal, los puntos de pendiente cero se encuentran en los puntos de error de seguimiento "y" máximo. Pero la igualdad es aproximadamente correcta siempre que la pendiente de "y" sea baja.
- Nótese que es negativo cuando "y" es positivo y al resvés. La otra ecuación para R, no es cierta cuando "y" se vuelve negativo, ya que no se permite que el radio R sea negativo (según su definición matemática). Pero después de que el radio R se elimina combinando las dos ecuaciones, la ecuación resultante se vuelve correcta al verificar los dos casos: "y" negativo e "y" positivo.
- Iwnicki, p.7 formula 2.1
- Carter, F.W. (25 de julio de 1928). «On the Stability of Running of Locomotives». Proceedings of the Royal Society. A 121 (788): 585-610. Bibcode:1928RSPSA.121..585C. doi:10.1098/rspa.1928.0220.
- Knothe, K. (2008). «History of wheel/rail contact mechanics: from Redtenbacher to Kalker». Vehicle System Dynamics 46 (1–2): 9-26. doi:10.1080/00423110701586469.
- Wickens, A.H. (1965–66). «The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability». Proc. Inst. Mech. Eng.: 29-.
- Wickens, A.H.; Gilchrist A.O.; A.E.W. Hobbs (1969–70). «Suspension Design for High-Performance Two-Axle Freight Vehicles». Proceedings of the Institution of Mechanical Engineers: 22-.
- Serajian, Reza (2013). «Parameters’ changing influence with different lateral stiffnesses on nonlinear analysis of hunting behavior of a bogie». Journal of Measurements in Engineering: 195-206.
- Serajian, Reza (2011). «Effects of the bogie and body inertia on the nonlinear wheel-set hunting recognized by the hopf bifurcation theory». Int J Auto Engng: 186-196.
Bibliografía
- Iwnicki, Simon (2006). Handbook of railway vehicle dynamics. CRC Press.
- Shabana, Ahmed A. (2008). Railroad vehicle dynamics : a computational approach. CRC Press.
- Wickens, A H (Jan 1, 2003). Fundamentals of rail vehicle dynamics : guidance and lateral stability. Swets & Zeitlinger.
- Serajian, Reza (2013). Parameters’ changing influence with different lateral stiffnesses on nonlinear analysis of hunting behavior of a bogie. CRC Press.
- Serajian, Reza (2011). Effects of the bogie and body inertia on the nonlinear wheel-set hunting recognized by the hopf bifurcation theory. CRC Press.