Semejanza (geometría)
En matemáticas se dice que dos figuras geométricas son semejantes si tienen la misma forma sin importar los tamaños entre ellos.
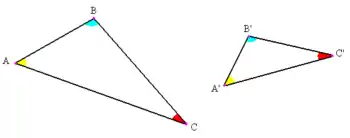

En geometría euclidiana, dos objetos son similares' si tienen la misma forma, o si uno tiene la misma forma que la imagen especular del otro. Más concretamente, uno puede obtenerse a partir del otro mediante escalado uniforme (ampliación o reducción), posiblemente con traslación, rotación y reflexión adicionales. Esto significa que cualquiera de los dos objetos puede reescalarse, reposicionarse y reflejarse, de modo que coincida exactamente con el otro objeto. Si dos objetos son similares, cada uno es congruente con el resultado de una determinada escala uniforme del otro.
 Translación |
 Rotación |
 Reflexión |
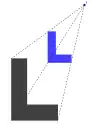 Escala |
Por ejemplo, todos los círculos son semejantes entre sí, todos los cuadrados son semejantes entre sí y todos los triángulos equiláteros son semejantes entre sí. En cambio, no todas las elipses son semejantes entre sí, ni todos los rectángulos son semejantes entre sí, ni todos los triángulos isósceles son semejantes entre sí. Esto se debe a que dos elipses pueden tener proporciones diferentes de anchura y altura, dos rectángulos pueden tener proporciones diferentes de longitud y anchura, y dos triángulos isósceles pueden tener ángulos de base diferentes.

Si dos ángulos de un triángulo tienen medidas iguales a las medidas de dos ángulos de otro triángulo, entonces los triángulos son semejantes. Los lados correspondientes de polígonos semejantes están en proporción, y los ángulos correspondientes de polígonos semejantes tienen la misma medida.
Dos congruentes formas son similares, con un factor de escala de 1. Sin embargo, algunos libros de texto escolares excluyen específicamente triángulos congruentes de su definición de triángulos similares, insistiendo en que los tamaños deben ser diferentes si los triángulos son para calificar como similar.
Introducción
Una semejanza entre dos figuras geométricas viene definida exclusivamente por la condición de que la distancia entre cualquier par de puntos de la primera figura y dividida entre la distancia de sus correspondientes puntos de la segunda figura y es constante, este valor se llama razón de semejanza :
La semejanza puede modificar el tamaño y la orientación de una figura, pero no altera su forma.[1]
Ecuación 1
Se reúnen estas dos propiedades equivalentes en la siguiente expresión:
Características
- Todos los triángulos equiláteros son semejantes.
- Si dos triángulos tienen dos ángulos iguales, los terceros también son iguales.
- Una semejanza es la composición de una isometría con una homotecia. En la semejanza se puede cambiar el tamaño y la orientación de una figura pero no se altera su forma.
Por lo tanto, dos triángulos son semejantes si tienen similar forma.
En el caso del triángulo, la forma solo depende de sus ángulos. Se puede simplificar así la definición: dos triángulos son semejantes si sus ángulos son iguales uno a uno.
En la figura, los ángulos correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos ABC y A'B'C' son semejantes se escribe ABC ~ A'B'C', donde el orden indica la correspondencia entre los ángulos: A, B y C se corresponden con A', B' y C', respectivamente. Una similitud tiene la propiedad de multiplicar todas las longitudes por un mismo factor. Por lo tanto las razones longitud imagen / longitud origen son todas iguales, lo que da una segunda caracterización de los triángulos semejantes: dos triángulos son semejantes si las razones de los lados correspondientes son congruentes.
Propiedad reflexiva, refleja o idéntica
Todo triángulo es semejante a sí mismo.
Propiedad idéntica o simétrica
Si un triángulo es semejante a otro, aquel es semejante al primero.
Propiedad transitiva
Si un triángulo es semejante a otro, y este a su vez es semejante a un tercero, el primero es semejante al tercero.
Estas tres propiedades implican que la relación de semejanza entre dos triángulos es una relación de equivalencia.
Teorema fundamental de la semejanza de triángulos
Todas las paralelas a un lado de un triángulo que no pase por el vértice opuesto, determina con las rectas a las que pertenecen los otros dos lados, un triángulo semejante al dado.
Hipótesis:
- Dado y
- corta o a su prolongación en
- corta o a su prolongación en
Tesis:
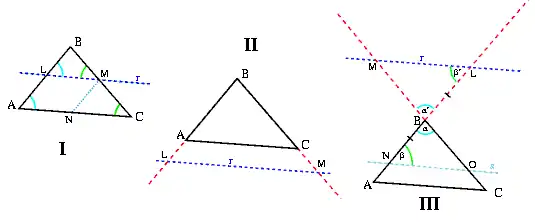
Dando lugar a tres casos:
Primer caso
Si corta a los lados AB y BC por puntos interiores a ellos:
Haremos una primera consideración, referida a los ángulos, y la llamaremos (1):
- por carácter reflejo
- por ser correspondientes entre r || AC, secante AB
- por ser correspondientes entre r || AC, secante BC
Por otra parte, en virtud del corolario del Teorema de Tales se tiene:
Si por M se traza una paralela al lado AB, esta interseca al lado AC en un punto N, y nuevamente por el corolario del Teorema de Tales tenemos:
Pero dado que AN = LM, por ser lados opuestos del paralelogramo ALMN, reemplazando en se obtiene:
- De y se obtiene la consideración que llamaremos (2):
Luego de (1) y (2), resulta:
- por definición de semejanza.
Segundo caso
r corta a las rectas de los lados AB y BC por puntos exteriores a ellos, sobre las semirrectas de origen B que los contienen.
Consideramos BLM como si fuera el triángulo dado, y BAC el triángulo nuevo, y por el caso I de la demostración, es:
- por carácter simétrico.
Tercer caso
Si corta los lados AB y BC en puntos que pertenecen a las semirrectas opuestas a las que sirven de sostén a dichos lados.
Sobre la semirrecta de origen B que contiene al punto A, se construye BN=BL y por el extremo N del segmento construido, una paralela a AC (s) que corta la recta de BC por O.
Quedan entonces por el caso I, semejanza que llamaremos .
Teniendo en cuenta los triángulos BNO y BLM, se observa:
- BN=BM por construcción
- α=α' por ser opuestos por el vértice.
- β=β' por ser alternos internos entre r || s, secante LN
Y siendo BNO=BLM es BNO ~ BLM por el primer corolario de la definición.
De y , y por carácter transitivo:
- BAC ~ BLM BLM ~ BAC
En el espacio euclídeo
Una semejanza (también llamada transformación de semejanza o similitud) de un espacio euclídeo es una biyección f del espacio sobre sí mismo que multiplica todas las distancias por el mismo número real positivo. r, de forma que para dos puntos cualesquiera x e y tenemos
donde "d(x,y)" es la distancia euclídea de x a y.[2] El escalar r tiene muchos nombres en la literatura incluyendo; la razón de similitud, el factor de estiramiento y el coeficiente de similitud. Cuando r = 1 una semejanza se llama una isometría (transformación rígida). Dos conjuntos se llaman semejantes si uno es imagen del otro bajo una semejanza.
Como mapa f : ℝn → ℝn, una semejanza de razón r toma la forma
Las semejanzas preservan planos, rectas, perpendicularidad, paralelismo, puntos medios, desigualdades entre distancias y segmentos de recta.[3] Las semejanzas conservan los ángulos pero no necesariamente la orientación, las semejanzas directas conservan la orientación y las semejanzas opuestas la cambian.[4]
Las semejanzas del espacio euclidiano forman un grupo bajo la operación de composición llamado el grupo de semejanzas S}.[5] Las semejanzas directas forman un subgrupo normal de S} y el grupo euclídeo E(n) de isometrías también forma un subgrupo normal.[6] El grupo de semejanzas S es a su vez un subgrupo del grupo afín, por lo que toda semejanza es una transformación afín.
Uno puede ver el plano euclidiano como el plano complejo,[7] es decir, como un espacio bidimensional sobre el reales. Las transformaciones de semejanza 2D pueden entonces expresarse en términos de aritmética compleja y vienen dadas por f(z) = az + b (similitudes directas) y f(z) = az + b (semejanzas opuestas), donde a y b son números complejos, a ≠ 0. Cuando a= 1, estas semejanzas son isometrías.
Relación de área y relación de volumen

La razón entre las áreas de figuras semejantes es igual al cuadrado de la razón de las longitudes correspondientes de dichas figuras (por ejemplo, cuando el lado de un cuadrado o el radio de un círculo se multiplica por tres, su área se multiplica por nueve, es decir, por tres al cuadrado). Las alturas de triángulos semejantes están en la misma proporción que los lados correspondientes. Si un triángulo tiene un lado de longitud b y una altitud trazada a ese lado de longitud h, entonces un triángulo semejante con el lado correspondiente de longitud kb tendrá una altitud trazada a ese lado de longitud kh. El área del primer triángulo es, A = 12bh, mientras que el área del triángulo semejante será A´ = 12(kb)(kh) = k2A. Las figuras semejantes que puedan descomponerse en triángulos semejantes tendrán áreas relacionadas de la misma manera. La relación es válida también para figuras que no son rectificables.
La relación entre los volúmenes de figuras semejantes es igual al cubo de la relación entre las longitudes correspondientes de dichas figuras (por ejemplo, cuando la arista de un cubo o el radio de una esfera se multiplican por tres, su volumen se multiplica por 27, es decir, por tres al cubo).
La ley del cubo cuadrado de Galileo se refiere a los sólidos semejantes. Si la razón de similitud (razón de lados correspondientes) entre los sólidos es k}, entonces la razón de superficies de los sólidos será k2, mientras que la razón de volúmenes será k3.
Geometrías no-euclídeas
La posibilidad de aumentar el tamaño de una figura sin modificar su forma es tan obvia y natural que durante milenios se pensó que era una consecuencia de los axiomas de la geometría, y se trató en vano de demostrarlo desde la Grecia antigua. Sin embargo, al estudiar otras geometrías, las no euclidianas, los matemáticos del siglo XIX, entre ellos Bernhard Riemann y Nikolái Lobachevski se dieron cuenta de que esto solo sucedía en los espacios euclídeos, es decir, sin curvatura.

Se puede definir una geometría sobre la esfera, por ejemplo: Los segmentos son los caminos más cortos que unen sus extremos y las rectas son las líneas geodésicas, a semejanza de los ecuadores de la esfera. El análogo de una homotecia se construye así: se escoge un punto O de la superficie como centro de la homotecia, y para definir la imagen de otro punto A se traza la geodésica que pasa por O y A (que es única si A no es el punto diametralmente opuesto a O), consideramos que O es el origen de esta línea y A el punto de abscisa 1. La imagen A' será el punto de abscisa k, donde k es la razón de la homotecia. En la figura se ha tomado k = 3 y se han construido las imágenes de B y C también.
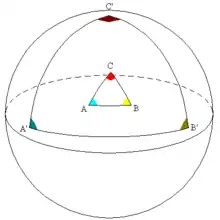
Se observa que la imagen del "triángulo" ABC es el "triángulo A'B'C', es decir que los catetos A'B', A'C' y B'C' son segmentos de líneas geodésicas, y que A'B'C' merece ser llamado triángulo semejante (por no decir homotético) al triángulo ABC.
Al aplicar la construcción precedente al pequeño triángulo ABC de la superficie de la esfera (pequeño en comparación con el diámetro), la suma de sus ángulos será ligeramente superior a π radianes (180°), pero el triángulo A'B'C' tendrá ángulos de mayor amplitud, siendo su suma mucho mayor que π radianes, como se ve en la figura. El aumento de tamaño implica aquí claramente un cambio de forma.
En conclusión, los triángulos semejantes permiten saber en que clase de espacio nos hallamos, uno euclidiano, o con curvatura positiva (como la esfera), o con curvatura negativa (espacio hiperbólico), y la doble caracterización de los triángulos similares (mismos ángulos y cocientes de los lados iguales) en la geometría usual no es ni anecdótico ni anodino.
Otros polígonos semejantes

El concepto de semejanza se extiende a polígonos con más de tres lados. Dados dos polígonos semejantes cualesquiera, los lados correspondientes tomados en la misma secuencia (aunque sea en el sentido de las agujas del reloj para un polígono y en el sentido contrario para el otro) son proporcionales y los ángulos correspondientes tomados en la misma secuencia son iguales en medida. Sin embargo, la proporcionalidad de los lados correspondientes no es suficiente por sí misma para demostrar la semejanza de los polígonos más allá de los triángulos (de lo contrario, por ejemplo, todos los rombos serían semejantes). Del mismo modo, la igualdad de todos los ángulos en secuencia no es suficiente para garantizar la similitud (de lo contrario, todos los rectángulos serían similares). Una condición suficiente para la semejanza de polígonos es que los lados y diagonales correspondientes sean proporcionales.
Para un n dado, todos los polígonos regulares n son semejantes.
Véase también
Referencias
- Real Academia de Ciencias Exactas, Física y Naturales, ed. (1999). Diccionario esencial de las ciencias. Espsa. ISBN 84-239-7921-0.
- Smart, 1998, p. 92.
- Yale, 1968, p. 47 Teorema 2.1.
- Pedoe, 1988, pp. 179-181.
- Yale, 1968, p. 46.
- Pedoe, 1988, p. 182.
- Este término tradicional, como se explica en su artículo, es un término equivocado. En realidad es la línea compleja unidimensional.
Bibliografía
- Henderson, David W.; Taimiņa, Daina (2005). Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd edición). Pearson Prentice-Hall. ISBN 978-0-13-143748-7.
- Jacobs, Harold R. (1974). Geometry. W. H. Freeman and Co. ISBN 0-7167-0456-0.
- Pedoe, Dan (1988). Geometry/A Comprehensive Course. Dover. ISBN 0-486-65812-0.
- Sibley, Thomas Q. (1998). The Geometric Viewpoint/A Survey of Geometries. Addison-Wesley. ISBN 978-0-201-87450-1. (requiere registro).
- Smart, James R. (1998). Modern Geometries (5th edición). Brooks/Cole. ISBN 0-534-35188-3.
- Stahl, Saul (2003). Geometry/From Euclid to Knots. Prentice-Hall. ISBN 978-0-13-032927-1.
- Venema, Gerard A. (2006). Foundations of Geometry. Pearson Prentice-Hall. ISBN 978-0-13-143700-5.
- Yale, Paul B. (1968). Geometry and Symmetry. Holden-Day.
Enlaces externos
- Weisstein, Eric W. «Similar». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.