Navegación ortodrómica

La navegación ortodrómica (del griego ὀρθός ‘recto’ y δρόμος ‘carrera’) o navegación por el círculo máximo, es la que sigue la distancia más corta entre dos puntos, es decir, es la que sigue un círculo máximo. Para realizar los cálculos de rumbo y distancia entre dos puntos es necesario resolver un triángulo esférico cuyos vértices son el origen, el destino y el polo.[1] Los lados que unen el polo con el origen y el destino son arcos de meridiano, y el lado que une el origen y el destino es el arco buscado. Su contrario es la navegación loxodrómica.

Ortodrómicas trazadas sobre un globo.

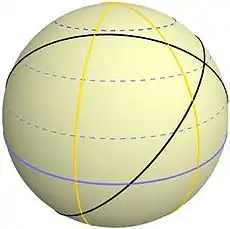
La ortodrómica es el arco de círculo máximo que corresponde a la distancia más corta entre dos puntos del globo y, dado que la Tierra es aproximadamente una esfera, la ortodrómica da a los navegantes la distancia más corta entre dos puntos (dados por su longitud y latitud) en un mapa, y el rumbo a tomar para ir del uno al otro. En un mapa plano, hecho con la proyección de Mercator, el rumbo aparece como un arco, en lugar de recto; ello se debe a la distorsión que la proyección de una superficie esférica sobre un plano.