Estado mixto

Un ejemplo de estados puros y mixtos es la polarización de la luz. Los fotones pueden tener dos helicidades, correspondientes a dos estados cuánticos ortogonales, ${\displaystyle {|R\rangle }}$ (polarización circular derecha) y ${\displaystyle {|L\rangle }}$ (polarización circular izquierda). Además, Un fotón puede estar en un estado de superposición, como ${\displaystyle {(|R\rangle +|L\rangle )/{\sqrt {2}}}}$ (polarización vertical) o ${\displaystyle {(|R\rangle -|L\rangle )/{\sqrt {2}}}}$ (polarización horizontal). De manera más general, puede estar en cualquier estado ${\displaystyle {(\alpha |R\rangle +\beta |L\rangle )/{\sqrt {2}}}}$ (con ${\displaystyle {\alpha ^{2}+\beta ^{2}=1}}$), sin embargo, la luz no polarizada (como la luz de una bombilla incandescente) no se corresponde con ningún estado del tipo ${\displaystyle {(\alpha |R\rangle +\beta |L\rangle )/{\sqrt {2}}}}$ (polarización lineal, circular o elíptica). A diferencia de la luz linealmente o elípticamente polarizada, la luz no polarizada pasa a través de un polarizador con una pérdida de intensidad del ${\displaystyle {50\%}}$ sea cual sea la orientación del polarizador, y a diferencia de la luz polarizada circularmente, no puede polarizarse linealmente con ninguna lámina de onda porque emergerá una polarización con orientación aleatoria.

La luz no polarizada se puede describir como un promedio en el que cada fotón puede tomar el estado ${\displaystyle {|R\rangle }}$ o ${\displaystyle {|L\rangle }}$ con un ${\displaystyle {50\%}}$ de probabilidad. Éste comportamiento es equivalente a una descripción en el que cada fotón puede estar polarizado vertical u horizontalmente con un ${\displaystyle {50\%}}$ de probabilidad, por lo tanto, la luz no polarizada no puede describirse a través de un estado puro, sino que debe ser descrita como un conjunto estadístico de, al menos, dos estados puros (los estados con polarización circular a izquierdas o a derechas, o bien los estados con polarización lineal vertical u horizontal). Estas dos descripciones son completamente indistinguibles experimentalmente, y por lo tanto se consideran el mismo estado mixto ya que describen una misma realidad física.

Una ventaja del uso de la matriz de densidad es que solo hay una matriz de densidad para cada estado mixto, mientras que hay muchos conjuntos estadísticos de estados puros para describir dicho estado mixo, de hecho la matriz de densidad contiene toda la información necesaria para calcular cualquier propiedad medible del estado mixto. ¿De dónde vienen los estados mixtos? Para responder eso se debe considerar cómo se puede generar luz no polarizada, a continuación se exponen tres formas de generar luz no polarizada:

• Una forma posible es usar un sistema en equilibrio térmico, una mezcla estadística de enormes cantidades de microestados, cada uno con una cierta probabilidad de realización (determinada por el factor Boltzmann), cambiando rápidamente de uno a otro debido a las fluctuaciones térmicas. La aleatoriedad térmica explica por qué una bombilla incandescente, por ejemplo, emite luz no polarizada.
• Una segunda forma que puede considerar de generar luz no polarizada es introducir incertidumbre en la preparación del sistema, por ejemplo, pasarla a través de un cristal birrefringente con una superficie rugosa, de modo que partes ligeramente diferentes del haz adquieran diferentes polarizaciones.
• Otro modo de generar luz no polarizada usa una configuración EPR: una desintegración radiactiva puede emitir dos fotones que viajan en direcciones opuestas, en el estado cuántico ${\displaystyle {(\alpha |R\rangle +\beta |L\rangle )/{\sqrt {2}}}}$ . Los dos fotones juntos están en un estado puro, pero si solo se toma uno de los fotones ignorando el otro, el fotón se comporta como la luz no polarizada.

De manera más general, los estados mixtos comúnmente surgen de una mezcla estadística del estado inicial (como en el equilibrio térmico), de incertidumbre en el procedimiento de preparación (como caminos ligeramente diferentes que un fotón puede viajar), o de observar un subsistema entrelazado con otro.

El vector de estado ${\displaystyle {|\psi \rangle }}$ de un estado puro determina completamente el comportamiento estadístico de una medición. Para la comprobación, tome una cantidad observable y permita que ${\displaystyle {A}}$ sea el operador observable asociado que tiene una representación en el espacio de Hilbert ${\displaystyle {\mathcal {H}}}$ del sistema cuántico. Para cualquier función analítica de valor real ${\displaystyle {F}}$ definida sobre los números reales, suponga que ${\displaystyle {F(A)}}$ es el resultado de aplicar ${\displaystyle {F}}$ al resultado de una medición. El valor esperado de ${\displaystyle {F(A)}}$ es:

${\displaystyle {\langle \psi |F(A)|\psi \rangle }}$

Ahora considere un estado mixto preparado mediante la combinación estadística de dos estados puros diferentes ${\displaystyle {|\psi \rangle }}$ y ${\displaystyle {|\phi \rangle }}$, con las probabilidades asociadas ${\displaystyle {p}}$ y ${\displaystyle {1-p}}$, respectivamente. Las probabilidades asociadas implican que el proceso de preparación, el sistema terminará en el estado ${\displaystyle {|\psi \rangle }}$ con probabilidad ${\displaystyle {p}}$ y en el estado ${\displaystyle {|\phi \rangle }}$ con probabilidad ${\displaystyle {1-p}}$. No es difícil mostrar que las propiedades estadísticas del observable para el sistema preparado en tal estado mixto están completamente determinadas, sin embargo, no existe ningún vector de estado ${\displaystyle {|\xi \rangle }}$ (ni siquiera ${\displaystyle {|\xi \rangle =p|\psi \rangle +(1-p)|\phi \rangle }}$, o ${\displaystyle {|\xi \rangle =p^{1/2}|\psi \rangle +(1-p)^{1/2}|\phi \rangle }}$) que determine este comportamiento estadístico de modo que el valor esperado de ${\displaystyle {F(A)}}$ sea

${\displaystyle {\langle \xi |F(A)|\xi \rangle }}$

Por otro lado, existe un operador único ${\displaystyle {\rho }}$ que permite describir valor esperado de ${\displaystyle {F(A)}}$ como: ${\displaystyle {\langle F(A)\rangle =\operatorname {tr} [\rho F(A)]}}$ donde el operador ${\displaystyle {\rho }}$ es el operador de densidad del sistema mixto. Un simple cálculo muestra que el operador ${\displaystyle {\rho }}$ en este caso está dado por

${\displaystyle {\rho =p|\psi \rangle \langle \psi |+(1-p)|\phi \rangle \langle \phi |}}$.

Para el ejemplo anterior de luz no polarizada, el operador de densidad es

${\displaystyle {\rho ={\tfrac {1}{2}}|R\rangle \langle R|+{\tfrac {1}{2}}|L\rangle \langle L|}}$.

En mecánica cuántica se llama operador densidad al objeto matemático correspondiente a un operador lineal que codifica todas las propiedades estadísticas de un sistema cuántico en la situación más general posible, en particular cuando no es posible describir el sistema mediante un estado puro. Para una base de funciones de onda concreta, se llama matriz densidad a la matriz que representa al operador densidad del sistema en dicha base. El operador se puede expresar como un operador en el espacio de Hilbert de los estados:

${\displaystyle \rho =\sum _{j}p_{j}\left|\psi _{j}\right\rangle \left\langle \psi _{j}\right|}$

${\displaystyle 0\leq p_{j}\leq 1;\sum _{j}p_{j}=1}$

donde ${\displaystyle {p_{j}}\,}$ es el peso de la función ${\displaystyle {\psi _{j}}\,}$ en el estado del sistema. Esto representa una mezcla estadística de estados puros. Si el sistema dado está aislado, entonces se puede pensar que un estado mixto representa un sistema único con un historial de preparación incierto, como se ha detallado anteriormente de forma explícita; o se puede considerar que el estado mixto representa un conjunto de sistemas, es decir, un gran número de copias del sistema en cuestión, donde ${\displaystyle {p_{j}}}$ es la fracción del conjunto que se encuentra en el estado ${\displaystyle {|\psi _{j}\rangle }}$.

Un conjunto se describe por estado puro si cada copia del sistema en ese conjunto está en el mismo estado, es decir, es un conjunto puro. Sin embargo, si el sistema no está aislado, no tiene sentido afirmar que el sistema tiene un estado definido pero desconocido, ya que el operador de densidad contiene toda la información sobre posibles entrelazamientos con otros sistemas físicos. Una función de onda pura ${\displaystyle {|\psi _{j}>}\,}$ tendrá el operador densidad ${\displaystyle {|\psi _{j}><\psi _{j}|}\,}$, que se puede ver como un operador de proyección. Solo para estados mezcla estrictos se cumple

${\displaystyle \rho ^{2}<\rho }$

y para estados puros:

${\displaystyle \rho ^{2}=\rho }$

En el caso de sistemas complejos, por ejemplo, un sistema de muchas moléculas idénticas en distintos estados, el valor esperado de cada propiedad física observable ${\displaystyle {A}}$ es la media de los valores propios, ponderada por ${\displaystyle p_{i}\,}$. Esto se suele expresar como la traza del observable por el operador densidad:

${\displaystyle \langle A\rangle =\sum _{j}p_{j}\langle \psi _{j}|A|\psi _{j}\rangle =\sum _{j}p_{j}\operatorname {tr} \left(|\psi _{j}\rangle \langle \psi _{j}|A\right)=\sum _{j}\operatorname {tr} \left(p_{j}|\psi _{j}\rangle \langle \psi _{j}|A\right)=\operatorname {tr} \left(\sum _{j}p_{j}|\psi _{j}\rangle \langle \psi _{j}|A\right)=\operatorname {tr} (\rho A)}$

donde, en una base ortonormal del espacio de las funciones de ondas,

${\displaystyle A_{kl}=<\phi _{k}|{\hat {A}}|\phi _{l}>}$

Además, si ${\displaystyle {A}}$ tiene resolución espectral:

${\displaystyle A=\sum _{i}a_{i}|a_{i}\rangle \langle a_{i}|=\sum _{i}a_{i}P_{i},}$

donde ${\displaystyle P_{i}=|a_{i}\rangle \langle a_{i}|}$, el operador de densidad correspondiente después de la medida está dada por:

${\displaystyle \;\rho '=\sum _{i}P_{i}\rho P_{i}.}$

Téngase en cuenta que el operador de densidad anterior describe el conjunto completo después de la medida. El subconjunto para el que el resultado de la medida ha sido el valor particular a_i es descrito por un operador de densidad diferente:${\displaystyle \rho _{i}'={\frac {P_{i}\rho P_{i}}{\operatorname {tr} [\rho P_{i}]}}.}$ Esto es cierto suponiendo que ${\displaystyle \textstyle |a_{i}\rangle }$ es el único estado proprio con valor proprio a_i; Más generalmente, P_i en esta expresión sería reemplazado por el operador de proyección en el subespacio proprio correspondiente al valor proprio a_i. De forma más general, se puede suponer que ${\displaystyle {\phi }}$ es una función que asocia a cada observable A un número ${\displaystyle {\phi (A)}}$, que se puede considerar como el "valor esperado" de A. Si ${\displaystyle {\phi }}$ satisface algunas propiedades naturales (como dar valores positivos en operadores positivos), entonces hay una matriz de densidad única ${\displaystyle {\rho }}$ tal que

${\displaystyle {\phi (A)=\operatorname {tr} (\rho A)}}$

para todos A. Es decir, cualquier "familia de valores esperados" es representable por una matriz de densidad. Esta observación sugiere que las matrices de densidad son la noción más general de un estado cuántico.

Para que un operador sea una matriz densidad, debe satisfacer varias propiedades. De hecho, cualquier operador que satisfaga estas propiedades es válido como matriz densidad:

1. ${\displaystyle {\mbox{Tr}}(\rho )=1}$ Esto viene del hecho de que ${\displaystyle {\mbox{Tr}}(\rho )={\mbox{Tr}}(\sum _{j}p_{j}|\psi _{j}\rangle \langle \psi _{j}|)=\sum _{j}p_{j}=1}$
2. ${\displaystyle \rho }$ debe ser hermítico, ρ = ρ^†.
3. ${\displaystyle \rho }$ debe ser definido positivo, ${\displaystyle \langle \psi |\rho |\psi \rangle \geq 0}$ para todo ${\displaystyle |\psi \rangle }$. Esto viene del hecho de que ${\displaystyle \langle \psi |\rho |\psi \rangle =\sum _{j}p_{j}|\langle \psi |\psi _{j}\rangle |^{2}\geq 0}$

También se puede ver que un operador es positivo si y solo si todos sus valores propios son mayores o iguales a cero, lo que implica que los valores propios de cualquier matriz densidad deben satisfacer esta propiedad. Además, como su traza vale 1 y esta es la suma de sus valores propios, se tiene que si ${\displaystyle \lambda _{j}}$ es un valor propio, entonces ${\displaystyle 0\leq \lambda _{j}\leq 1}$. Ahora se utiliza todo esto para buscar propiedades adicionales. La primera es una forma simple de identificar estados puros.

Teorema. La matriz densidad ${\displaystyle \rho }$ es un estado puro si y solo sí

${\displaystyle {\mbox{Tr}}(\rho ^{2})=1}$.

Demostración. Si ${\displaystyle \rho }$ es pura, entonces ${\displaystyle \rho =|\psi \rangle \langle \psi |}$, y ${\displaystyle \rho ^{2}=\rho }$. Inmediatamente esto implica que ${\displaystyle {\mbox{Tr}}(\rho ^{2})=1}$. Como ${\displaystyle \rho }$ es hermítico, se puede expresar como:

${\displaystyle \rho =\sum _{j}\lambda _{j}P_{j}}$

donde ${\displaystyle \lambda _{j}}$ son los valores propios distintos de cero de ${\displaystyle \rho }$, y los ${\displaystyle P_{j}}$ son las correspondientes proyecciones espectrales. Esto implica que

${\displaystyle \rho ^{2}=\sum _{j}\lambda _{j}^{2}P_{j}}$

Denotando el rango de ${\displaystyle P_{j}}$ por ${\displaystyle n_{j}}$ se tiene que

${\displaystyle {\mbox{Tr}}(\rho )=1\to \sum _{j}\lambda _{j}n_{j}=1}$ :${\displaystyle {\mbox{Tr}}(\rho ^{2})=1\to \sum _{j}\lambda _{j}^{2}n_{j}=1}$

y de estas dos ecuaciones

${\displaystyle \sum _{j}(\lambda _{j}-\lambda _{j}^{2})n_{j}=0}$

Como cada valor propio está entre 0 y 1, cada término en la suma anterior es mayor o igual a cero, lo que implica además que cada término debe ser igual a cero. La única forma de que esto ocurra es si cada ${\displaystyle \lambda _{j}}$ es igual a 0 o 1, y se ha asumido que ${\displaystyle \lambda _{j}>0}$, entonces ${\displaystyle \lambda _{j}=1}$. Esto junto con el hecho de que la suma de los valores propios por su mutiplicidad es uno, es consistente solo si uno de ellos es distinto de cero, y este valor propio tiene multiplicidad 1. Entonces ${\displaystyle \rho }$ es igual a una proyección de rango uno, lo que significa que es un estado puro.

Esfera de Bloch.

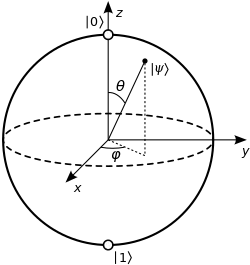
La esfera de Bloch es una representación para vectores estado de qubits, o lo que es lo mismo, estados puros de un qubit. Si se extiende esta representación incluyendo el interior de la esfera, se puede utilizar también para representar estados mixtos de qubits. Para ver esto, se puede expandir una matriz de densidad de qubit, que es una matriz de 2 × 2, en términos de la matriz de identidad y las matrices de Pauli, que forman una base completa para el espacio de un conjunto de matrices de 2 × 2:

${\displaystyle \rho ={\frac {1}{2}}(I+n_{x}\sigma _{x}+n_{y}\sigma _{y}+n_{z}\sigma _{z})}$Esto satisface la condición ${\displaystyle {\mbox{Tr}}(\rho )=1}$, y el hecho de que

${\displaystyle \rho }$ es hermítico implica que ${\displaystyle n_{x},n_{y}}$ y ${\displaystyle n_{z}}$ son reales. De esta misma ecuación se tiene que

${\displaystyle \rho ={\frac {1}{2}}{\begin{pmatrix}1+n_{z}&n_{x}-in_{y}\\n_{x}+in_{y}&1-n_{z}\end{pmatrix}}.}$

que además implica que ${\displaystyle det(\rho )=(1-|n|^{2})/4}$. Que ${\displaystyle \rho }$ sea positivo significa que su determinante debe ser mayor o igual a cero, por lo tanto ${\displaystyle 1\geq |n|}$. Se representa la matriz de densidad ${\displaystyle \rho }$ a través del vector n, que se encuentra en la esfera unidad. Por otra parte se sabe que si ${\displaystyle \rho }$ es un estado puro, su vector correspondiente tendrá su punto final en la superficie de la esfera de Bloch.

Por otra parte se demuestra el caso contrario. Si ${\displaystyle |n|=1}$ entonces ${\displaystyle {\mbox{Tr}}(\rho )=1}$ y ${\displaystyle det(\rho )=0}$. Esto implica que uno de los valores propios de ${\displaystyle \rho }$ es cero y el otro es uno. Si ${\displaystyle |u\rangle }$ es el vector propio con valor propio 1, donde ${\displaystyle ||u||=1}$, entonces ${\displaystyle \rho =|u\rangle \langle u|}$, y es estado puro. Dada una matriz de densidad de qubit, ${\displaystyle \rho }$, se puede encontrar fácilmente el vector correspondiente. La identidad ${\displaystyle {\mbox{Tr}}(\sigma _{j}\sigma _{k})=\delta _{jk}}$, donde j, k ∈ {x,y,z}, nos da que

${\displaystyle n_{j}={\mbox{Tr}}(\rho \sigma _{j})}$

La mayoría de las matrices densidad suelen corresponder a muchos conjuntos diferentes. A continuación se exponen algunos ejemplos.

En el primer ejemplo, se definen los estados

${\displaystyle |\pm x\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle \pm |1\rangle )}$

los cuales son estados propios de ${\displaystyle \sigma _{x}}$. Entonces se puede escribir la matriz densidad de un estado mixto máximo de dos maneras:

${\displaystyle \rho ={\frac {1}{2}}I={\frac {1}{2}}(|0\rangle \langle 0|+|1\rangle \langle 1|)={\frac {1}{2}}(|+x\rangle \langle +x|+|-x\rangle \langle -x|)}$.

La primera descomposición corresponde a un conjunto en el que la mitad de los elementos están en el estado ${\displaystyle |0\rangle }$ y la mitad en el estado ${\displaystyle |1\rangle }$, y el segundo corresponde a un conjunto en el que la mitad de los elementos están en el estado ${\displaystyle |+x\rangle }$ y la mitad en el estado ${\displaystyle |-x\rangle }$. Estos conjuntos son diferentes, pero están descritos por la misma matriz de densidad.

En el segundo ejemplo, se definen los estados

${\displaystyle |u_{\pm }\rangle ={\frac {1}{\sqrt {4\pm 2{\sqrt {2}}}}}[({\sqrt {2}}\pm 1)|0\rangle \pm |1\rangle ]}$.

Entonces: ${\displaystyle \rho ={\frac {1}{2}}(|0\rangle \langle 0|+|+x\rangle \langle +x|)=({\frac {1}{2}}+{\frac {\sqrt {2}}{4}})(|u_{+}\rangle \langle u_{+}|+({\frac {1}{2}}-{\frac {\sqrt {2}}{4}})|u_{-}\rangle \langle u_{-}|)}$, describiendo de nuevo dos conjuntos diferentes por la misma matriz densidad. En general, si ${\displaystyle \rho _{1}}$ y ${\displaystyle \rho _{2}}$ son matrices densidad, de la forma

${\displaystyle \rho (\theta )=\theta \rho _{1}+(1-\theta )\rho _{2}}$,

donde ${\displaystyle 0\leq \theta \leq 1}$. Esto implica que el conjunto de matrices densidad es convexo. La mayoría de las matrices densidad se pueden expresar como una descomposición en otras matrices densidad la cual se puede realizar de distintas formas, y cada una de estas descomposiciones corresponderá, en general, a un conjunto diferente. Los dos ejemplos anteriores son solo casos particulares de esta afirmación general. Esto, sin embargo, no es cierto para los estados puros; éstos tienen una descomposición única. Para verlo se supondrá que ${\displaystyle \rho =|\psi \rangle \langle \psi |}$ es un estado puro de la matriz densidad y también que puede ser expresado como una suma de otras dos matrices densidad, ${\displaystyle \rho (\theta )=\theta \rho _{1}+(1-\theta )\rho _{2}}$. Entonces si ${\displaystyle |\psi _{\bot }\rangle }$ satisface ${\displaystyle \langle \psi _{\bot }|\psi \rangle =0}$, se tiene que

${\displaystyle 0=\langle \psi _{\bot }|\rho (\theta )|\psi _{\bot }\rangle =\theta \langle \psi _{\bot }|\rho _{1}|\psi _{\bot }\rangle +(1-\theta )\langle \psi _{\bot }|\rho _{2}|\psi _{\bot }\rangle }$.

Como ambos términos en el lado derecho son ≥ 0, se deduce que

${\displaystyle \langle \psi _{\bot }|\rho _{1}|\psi _{\bot }\rangle =\langle \psi _{\bot }|\rho _{2}|\psi _{\bot }\rangle =0}$.

Esta ecuación es cierta para cualquier vector ortogonal a ${\displaystyle |\psi \rangle }$, por lo tanto, ${\displaystyle \rho _{1}=\rho _{2}=|\psi \rangle \langle \psi |}$ y se concluye que la representación de cualquier estado puro es única. Los estados puros no se pueden expresar como una suma de otras matrices densidad. Estos son los únicos estados que cumplen esta propiedad, ya que si ${\displaystyle \rho }$ representa un estado mixto, que está dada por ${\displaystyle \rho =\sum _{j}p_{j}|\psi _{j}\rangle \langle \psi _{j}|}$, que no es más que una suma de estados puros.