Figura isogonal

En geometría, un politopo (como un polígono, un poliedro o un teselado) es isogonal o transitivo en sus vértices si todos sus vértices son equivalentes bajo las simetrías de la figura. Esto implica que cada vértice está rodeado por los mismos tipos de caras en el mismo orden o en el orden inverso, y con los mismos ángulos entre las caras correspondientes.

Rombicuboctaedro, ejemplo de un poliedro isogonal
Girobicúpula cuadrada elongada, ejemplo de un poliedro no isogonal

Técnicamente, se dice que para cualquier par de vértices, existe una simetría cuando se realiza una aplicación politópica isométrica del primero sobre el segundo. Otra forma de decir esto es que el grupo de automorfismos del politopo es transitivo en sus vértices, o que los vértices descansan dentro de la misma órbita de simetría.

Todos los vértices de una figura isogonal finita n-dimensional existen en una (n-1)-esfera.

El término "isogonal" se ha usado durante mucho tiempo para poliedros. "Transitivo en sus vértices" es un sinónimo tomado de ideas modernas, como los grupos de simetrías y la teoría de grafos.

La girobicúpula cuadrada elongada, que es no isogonal, demuestra que simplemente afirmar que todos los vértices tienen el mismo aspecto no es una condición tan restrictiva como la definición utilizada aquí, que involucra el grupo de isometrías que preservan el poliedro o el teselado.

Polígonos y apeirógonos isogonales
Apeirógonos isogonales
Apeirógonos oblicuos isogonales

Todos los polígonos regulares, apeirógonos y polígonos regulares estrellados son isogonales. El dual de un polígono isogonal es un polígono isotoxal.

Algunos polígonos de lados pares y apeirógonos que alternan dos longitudes de borde, como por ejemplo un rectángulo, también son isogonales.

Todos los 2n-gonos isogonales planos forman parte de un grupo diedral (Dn, n = 2, 3, ...) con líneas de reflexión en los puntos medios de cada lado.

D2 D3 D4 D7

Rectángulos isogonales y rectángulos cruzados compartiendo la misma disposición de vértices
Hexagrama isogonal con 6 vértices idénticos y dos longitudes de lados.[1]
Octógono convexo isogonal, con líneas de reflexión radiales azules y rojas
Tetradecágono "estrellado" isogonal, con un tipo de vértices, y con dos tipos de aristas[2]

Poliedros isogonales y teselados 2D
Teselados isogonales
Teselado cuadrado distorsionado
Teselado cuadrado truncado y distorsionado

Un poliedro y un teselado 2D isogonales tienen un solo tipo de vértices. Un poliedro isogonal con todas las caras regulares también es un poliedro uniforme y puede representarse mediante una notación de configuración de vértices que secuencia las caras alrededor de cada vértice. Asimismo, se puede dar a la configuración de los vértices de los poliedros variaciones distorsionadas geométricamente e inclinaciones uniformes.

Poliedros isogonales
D3d, orden 12 Th, orden 24 Oh, orden 48
4.4.6 3.4.4.4 4.6.8 3.8.8

Un prisma hexagonal distorsionado
Un rombicuboctaedro distorsionado
Un cuboctaedro truncado someramente
Un cubo híper-truncado

Los poliedros isogonales y los teselados 2D pueden clasificarse adicionalmente como:

  • Regulares si también son isoedrales (transitivos de caras) y isotoxales (transitivo de aristas); esto implica que cada cara es del mismo tipo de polígono regular.
  • Cuasi-regulares si también son de aristas uniformes (transitivo de aristas) pero no isoedrales (transitivos de caras).
  • Semirregulares si cada cara es un polígono regular, pero no son isoedrales (transitivos de caras) o de aristas uniformes (transitivos de aristas) (la definición varía entre distintos autores, por ejemplo, algunos excluyen sólidos con simetría diedral o sólidos no convexos).
  • Uniforme si cada cara es un polígono regular, es decir, es regular, cuasiregular o semirregular.
  • Semi-uniforme si sus elementos también son isogonales.
  • Escaliforme si todas las aristas tienen la misma longitud.
  • Noble si también son isoedrales (transitivos de caras).

Politopos y teselaciones isogonales

Estas definiciones se pueden extender a politopos de mayor dimensión y teselaciones. En general, todos los politopos uniformes son isogonales, por ejemplo, los 4-politopos uniformes y los panales convexos uniformes.

El dual de un politopo isogonal se denomina isótopo, que es transitivo en sus facetas.

Figuras k-isogonales y k-uniformes

Un politopo o teselado se puede llamar k-isogonal si sus vértices forman k clases de transitividad. Un término más restrictivo, k-uniforme, se define como una figura k-isogonal si está construida solo a partir de polígonos regulares. Se pueden representar visualmente con un color por cada clase.


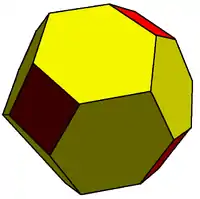Este rombododecaedro truncado es 2-isogonal porque contiene dos clases de vértices transitivos. Esta poliedro está formado por cuadrados y hexágonos achatados.
Este teselado semiregular es también 2-isogonal (y 2-uniforme). Está formado por triángulos equiláteros y hexágonos regulares.
Eneagrama {9⁄4} 2-isogonal

Véase también

Referencias
  1. Coxeter, The Densities of the Regular Polytopes II, p54-55, "hexagram" vertex figure of h{5/2,5}.
  2. The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum, Figure 1. Parameter t=2.0
  • Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 0-521-55432-2, p. 369 Transitividad
  • Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. (p. 33 k-isogonal mosaico, p. 65 k-uniform tiles )

Enlaces externos


Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.