Politopo regular convexo de 4 dimensiones

Estos politopos fueron descritos por primera vez por el matemático suizo Ludwig Schläfli a mediados del siglo XIX. Schläfli descubrió que hay precisamente 6 de estas figuras. Cinco de ellas pueden pensarse como análogos de los sólidos platónicos en mayor número de dimensiones. Hay una figura adicional, el icositetracoron o 24-cell, que no tiene un equivalente tridimensional.

Cada politopo regular convexo tetradimensional está delimitado por un conjunto de celdas tridimensionales, que son todas sólidos platónicos del mismo tipo y tamaño. Se agrupan a lo largo de sus respectivas caras de modo regular.

Nombre	Familia	Símbolo de Schläfli	Vértices	Aristas	Caras	Celdas	Figuras de vértices	Politopo dual	Imagen
pentácoron	simplex	{3,3,3}	5	10	10 triángulos	5 tetraedros	tetraedros	(auto-dual)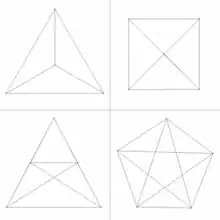
octácoron, teseracto	politopo de medida	{4,3,3}	16	32	24 cuadrados	8 cubos	tetraedros	hexadecacoron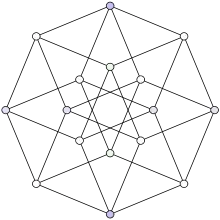
hexadecacoron o 16-cell	politopo de cruce	{3,3,4}	8	24	32 triángulos	16 tetraedros	octaedros	teseracto
icositetracoron o 24-cell		{3,4,3}	24	96	96 triángulos	24 octaedros	cubos	(auto-dual)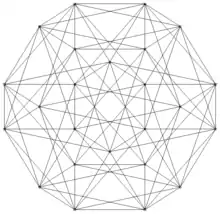
hecatonicosacoron o 120-cell		{5,3,3}	600	1200	720 pentágonos	120 dodecaedros	tetraedros	Hexacosicoron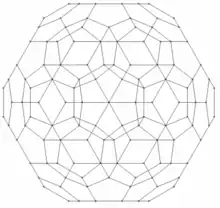
hexacosicoron o 600-cell		{3,3,5}	120	720	1200 triángulos	600 tetraedros	icosaedros	Hecatonicosacoron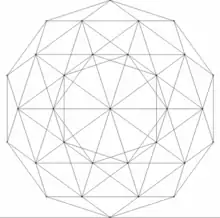

Nótese que puesto que cada una de estas figuras es topológicamente equivalente a una 3-esfera, cuya característica de Euler es cero, tenemos el análogo tetradimensional de la fórmula poliédrica de Euler

${\displaystyle N_{0}-N_{1}+N_{2}-N_{3}=0}$

donde N_k denota el número de k-caras del politopo (un vértice es una 0-cara, una arista es una 1-cara, etc.).

• Politopo regular
• Sólido platónico

• H. S. M. Coxeter, Introduction to Geometry, 2nd ed., John Wiley & Sons Inc., 1969. ISBN 0-471-50458-0.

• Descomposiciones de politopos regulares 4D (en inglés).
• Tutorial del hiperespacio, varias visualizaciones de politopos regulares tetradimensionales (en inglés).

La versión original de este artículo es una traducción de en:Convex regular 4-polytope en Wikipedia en inglés