Retículo distributivo
En matemática, un retículo distributivo es un retículo en el cual las operaciones de unión (join) e intersección (meet) se distribuyen la una sobre la otra. El ejemplo típico de estas estructuras es una colección de conjuntos, donde los operadores quedan dados por la unión de conjuntos y la intersección de conjuntos. De hecho, dicho ejemplo describe el escenario por completo: todo retículo distributivo es isomorfo a un retículo de conjuntos.
Definición formal
Como en el caso de los retículos arbitrarios, un retículo distributivo L puede definirse equivalentemente como una estructura desde el punto de vista de la teoría del orden o del álgebra universal.
Definición algebraica
Un retículo (L,, ) es distributivo si lo siguiente se cumple para todo x, y, z en L:
Viendo los retículos como conjuntos parcialmente ordenados, se dice que el operador meet "preserva" un número finito y no vacío de operadores join. Un resultado básico de la teoría de retículos es que la condición de arriba es equivalente a su dual:
Otra definición equivalente es decir que L es distributivo si y sólo si lo siguiente se cumple para cualesquiera elementos x, y, z en L:
Lo que a su vez es equivalente a decir
- y implica .
Morfismos
Un morfismo de retículos distributivos es una función que es compatible con los dos operadores meet y join.
Ejemplos
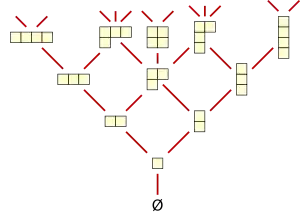
Los retículos distributivos son estructuras ubicuas y al mismo tiempo muy específicas. El ejemplo típico es la familia de conjuntos provista de los operadores de unión e intersección. Otros ejemplos son:
- Toda Álgebra de Boole es un retículo distributivo.
- El Álgebra de Lindenbaum–Tarski de la lógica, donde el operador de conjunción se distribuye sobre el de disyunción, y viceversa.
- Toda Álgebra de Heyting es un retículo distributivo. Este incluye especialmente a los retículos locales, y por tanto a todos los retículos de conjuntos abiertos de los espacios topológicos. Las álgebras de Heyting pueden verse como Álgebras de Lindenbaum de lógica intuicionista, lo que lo convierte en un caso particular del ejemplo anterior.
- Los conjuntos totalmente ordenados con el máximo como join y el mínimo como meet.
- Los números naturales conforman un retículo distributivo completo, con el máximo común divisor como meet y el mínimo común múltiplo como join.
- Dado un entero positivo n, el conjunto de todos los divisores positivos de n, con el máximo común divisor y el mínimo común múltiplo como meet y join, respectivamente. Esta es un álgebra booleana sí y sólo si n es un entero libre de cuadrados.
- Un espacio vectorial reticular ordenado, comúnmente llamado espacio de Riesz.
- El retículo de Young dado por la inclusión que ordena la tabla de Young representando particiones enteras.
Propiedades
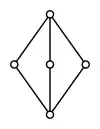
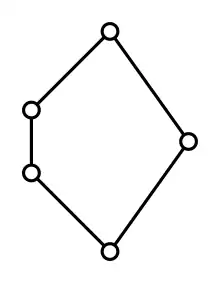
Los retículos no-distributivos más simples son el "retículo diamante", M3, y el "retículo pentágono", N5. Un retículo es distributivo si y sólo si ninguno de sus subretículos es isomorfo a M3 o N5; un subretículo es un subconjunto cerrado bajo los operadores meet y join del retículo original.
Un elemento de un retículo distributivo es meet-primo o ínfimo-primo si y sólo si es meet-irreducible o ínfimo-irreducible, aunque esta última se considera en general una propiedad más débil. Por dualidad, lo mismo es cierto para los elementos join-primo (supremo-primo) y join-irreducibles (supremo-irreducibles).[1] Si un retículo es distributivo, su relación de cobertura forma un grafo mediano.[2]
Finalmente, todo retículo distributivo es también modular.
Teoría de la representación
En la introducción se señaló la caracterización más importante para los retículos distributivos. Dado un retículo L:
|
Que la unión e intersección son distributivas en el sentido de arriba, es decir, afirmar que se cumple el bicondicional de derecha a izquierda, es un hecho elemental. La implicación en sentido contrario es menos trivial, pues requiere de teoremas de representación. La idea de esta caracterización es que las identidades o ecuaciones que se mantienen en todos los retículos distributivos son exactamente las mismas que se cumplen en todos los retículos de conjuntos descritos anteriormente.
El Teorema de representación de Birkhoff para retículos distributivos establece que todo retículo distributivo finito es isomorfo al retículo de conjuntos superiores del poset de sus elementos join-primos (o equivalentemente, join-irreducibles). Esto establece una biyección (salvo isomorfismo) entre la clase de todos los posets y la clase de todos los retículos distributivos finitos. Esta biyección puede extenderse a una dualidad de categorías entre homomorfismos de retículos distributivos finitos y funciones monótonas de posets finitos. Generalizar estos resultados a retículos infinitos, sin embargo, requiere del uso de estructuras adicionales.
Otro antiguo teorema de representación es ahora conocido como el Teorema de representación de Stone para retículos distributivos (llamado así en honor a Marshall Harvey Stone, quien fue el primero en demostrarlo). Este teorema caracteriza retículos distributivos como retículos de conjuntos abiertos compactos de ciertos espacios topológicos. Este resultado puede ser visto como una generalización del Teorema de representación de Stone para álgebras booleanas y como una especialización del marco general de la dualidad de Stone.
Una representación importante fue establecida por Hilary Priestley en su Teorema de representación de Priestley para retículos distributivos. En esta formulación, un retículo distributivo se utiliza para construir un espacio topológico con un orden parcial adicional sobre sus puntos, obteniendo un espacio de Stone ordenado (o espacio de Priestley). El retículo original es recuperado como la colección de conjuntos clopen inferiores en este espacio.
Como consecuencia de los teoremas de Stone y de Priestley, es fácil deducir que cualquier retículo distributivo es realmente isomorfo a un retículo de conjuntos. Sin embargo, las demostraciones de ambas aseveraciones requieren del teorema del primo ideal booleano, una forma débil del axioma de elección.
Retículos distributivos libres
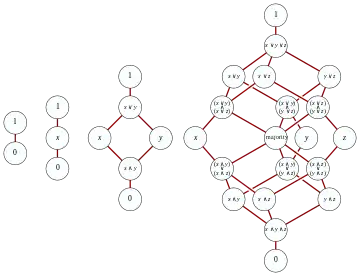
El retículo distributivo libre sobre un conjunto de generadores G puede construirse más fácilmente que un retículo libre general. Una primera observación es que, usando las propiedades de distributividad, cada término formado por los operadores binarios y en un conjunto de generadores puede ser transformado equivalentemente en la siguiente forma normal:
- M1 M2 ... Mn
donde Mi son meets finitos de elementos de G. Además, como el meet y el join son conmutativos e idempotentes, se pueden ignorar los órdenes y los duplicados, para así representar un join de meets como el de arriba como un conjunto de conjuntos:
- {N1, N2, ..., Nn},
donde Ni son subconjuntos finitos de G. Sin embargo, es todavía posible que dos de estos términos denoten el mismo elemento de retículos distributivos. Esto ocurre cuando existen índices j y k tales que Nj es un subconjunto de Nk. En este caso el meet de Nk estará debajo del meet de Nj, y por lo tanto se puede retirar con seguridad el conjunto redundante Nk sin cambiar la representación del término total. En consecuencia, un conjunto de subconjuntos finitos de G se llamará irredundante siempre que todos sus elementos Ni sean mutuamente incomparables (con respecto al ordenamiento del subconjunto); lo que se cumple cuando este forma una anticadena de conjuntos finitos.
Ahora el retículo distributivo libre sobre un conjunto de generadores G es definido como el conjunto de todos los conjuntos irredundantes finitos de subconjuntos de G (o lo que es lo mismo, como un hipergrafo irredundante). El join de dos conjuntos finitos irredundantes se obtiene de sus uniones removiendo todos los conjuntos redundantes. Asimismo, el meet de dos conjuntos S y T es la versión irredundante de { NM | N en S, M en T}. Esta estructura es un retículo distributivo con la requerida propiedad universal.
El número de elementos en un retículo distributivo libre con n generadores está dado por los números de Dedekind. Estos números crecen rápidamente, y son conocidos sólo para n ≤ 8; estos son
Los números de arriba cuentan el número de estos retículos en que las operaciones son uniones e intersecciones de conjuntos de elementos finitos, incluyendo al conjunto vacío. Si no permitimos las uniones e intersecciones vacías, el retículo distributivo libre tiene dos elementos menos; sus números de elementos forman la secuencia
Referencias
Notas
- Edelman, Paul H. (1980), «Meet-distributive lattices and the anti-exchange closure», Algebra Universalis 10 (1): 290-299, doi:10.1007/BF02482912..
- Birkhoff, Garrett; Kiss, S. A. (1947), «A ternary operation in distributive lattices», Bulletin of the American Mathematical Society 52 (1): 749-752, doi:10.1090/S0002-9904-1947-08864-9, MR 0021540..
Bibliografía
- Burris, Stanley N., y H.P. Sankappanavar, H. P., 1981. A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.