Simetría especular (teoría de cuerdas)

Los objetos fundamentales de la teoría de cuerdas son cuerdas abiertas y cerradas.

En física, la teoría de cuerdas es un marco teórico en el que las partículas asimiladas a puntos de la física de partículas se sustituyen por objetos unidimensionales llamados cuerdas. Estas cuerdas se visualizan como pequeños segmentos o bucles de cuerda ordinaria. La teoría de cuerdas describe cómo las cuerdas se propagan a través del espacio e interactúan entre sí. A escalas mucho mayores que la de la cuerda, esta se verá como una partícula ordinaria, con su masa, carga y otras propiedades determinadas por el estado de vibración de la cuerda. Las interacciones entre partículas, explicadas convencionalmente como procesos de emisión y absorción de estas, se describen bajo el nuevo planteamiento como la división y recombinación de cuerdas.[nb 1]

Hay diferencias notables entre el mundo descrito por la teoría de cuerdas y el mundo cotidiano. En la vida diaria, hay tres dimensiones espaciales conocidas —arriba/abajo, izquierda/derecha y adelante/atrás— y una dimensión de tiempo ―después/antes―. Así, en el lenguaje de la física moderna, se dice que el espacio-tiempo es de cuatro dimensiones o cuatridimensional.[1] Una de las características peculiares de la teoría de cuerdas es que requiere dimensiones adicionales para su consistencia matemática. En la versión que incorpora un planteamiento hipotético llamado supersimetría a la teoría de supercuerdas, hay seis dimensiones espaciales adicionales además de las cuatro conocidas, dando lugar a un espacio-tiempo de diez dimensiones.[2]

Uno de los objetivos de la investigación en la teoría de cuerdas es el desarrollo de modelos consistentes con las propiedades de las partículas observadas en experimentos de física de alta energía. Puesto que su espacio-tiempo debe ser de cuatro dimensiones a la escala del experimento, se debe buscar la manera de restringir las dimensiones adicionales a escalas más pequeñas. En los modelos más realistas basados en la teoría de cuerdas, esto se logra mediante un proceso llamado compactación, en el que se supone que las dimensiones extra se curvan sobre sí mismas para formar círculos.[3] En el límite, donde estas dimensiones enroscadas llegan a ser muy pequeñas, se obtiene un modelo en el que el espacio-tiempo tiene, a efectos prácticos, un menor número de dimensiones. Una analogía común para visualizar esta situación es considerar un objeto multidimensional como una manguera de jardín. Si la manguera se observa a cierta distancia, parece tener sólo una dimensión, su longitud. Sin embargo, a medida que el observador se acerca a ella, descubre que posee una segunda dimensión, su circunferencia.[nb 2] Por tanto, una hormiga caminando en la superficie de la manguera se movería en dos dimensiones.[nb 3]

Una sección transversal de una variedad de Calabi-Yau de quinto grado

La compactación puede ser utilizada para construir modelos en los que, a efectos prácticos, el espacio-tiempo es de cuatro dimensiones. Sin embargo, no todas las formas de compactar las dimensiones extra producen un modelo con las propiedades adecuadas para describir el mundo natural que observamos. Para obtener un modelo viable, las dimensiones compactadas deben formar una variedad de Calabi-Yau.[3] Esta variedad es un espacio especial que se considera generalmente de seis dimensiones en aplicaciones a la teoría de cuerdas. Recibe su nombre de los matemáticos Eugenio Calabi y Shing-Tung Yau.[4]

Cuando las variedades de Calabi-Yau entraron en la física de cuerdas como una forma de compactar dimensiones adicionales, comenzaron a despertar interés en el ámbito de la física. A finales de la década de 1980, Lance Dixon, Wolfgang Lerche, Cumrun Vafa y Nick Warner notaron que para una compactación dada de la teoría de cuerdas, no era posible reconstruir de forma única la correspondiente variedad de Calabi-Yau.[5][6] En cambio, en dos versiones diferentes conocidas como teoría de cuerdas de tipo IIA y tipo IIB, las dimensiones pueden ser compactadas en variedades de Calabi-Yau completamente diferentes, que dan lugar a las mismas propiedades físicas.[nb 4] En esta situación, reciben el nombre de variedades especulares, y la relación entre las dos teorías físicas se denomina simetría especular.[7]

La relación de simetría especular es un ejemplo particular de lo que los físicos llaman una dualidad. En general, este término se refiere a una situación en la que dos teorías físicas aparentemente diferentes resultan ser equivalentes en una forma no trivial. Si una hipótesis se puede transformar para asemejarla a otra teoría, se dice que son duales en virtud de esa transformación. Así pues, las dos conjeturas son descripciones matemáticamente diferentes de los mismos fenómenos.[8] Estas dualidades juegan un papel importante en la física moderna, sobre todo en la teoría de cuerdas.[nb 5]

Independientemente de que las compactaciones Calabi-Yau de la teoría de cuerdas proporcionen una descripción correcta de la naturaleza, la existencia de la dualidad especular entre las diferentes teorías de cuerdas tiene consecuencias de interés para las matemáticas puras.[9] Por ejemplo, la simetría especular permite a los expertos resolver problemas en la geometría algebraica enumerativa, una rama de las matemáticas que se ocupa de contar el número de soluciones a las cuestiones geométricas. Un problema clásico de la geometría enumerativa es enumerar las curvas racionales en una variedad Calabi-Yau. Mediante la aplicación de la simetría especular, el problema se plantea en una variedad Calabi-Yau diferente, donde es más fácil de resolver.[10]

En la teoría de cuerdas, la simetría especular se justifica con un razonamiento basado en la física.[11] Sin embargo, los matemáticos generalmente requieren pruebas rigurosas que no necesiten de una apelación a la intuición física. Desde un punto de vista matemático, la versión de la simetría especular descrita anteriormente es todavía solo una conjetura, pero hay otra versión de esta en el contexto de la teoría de cuerdas topológica, una variante simplificada de la teoría de cuerdas introducida por Edward Witten,[12] que ha sido detalladamente comprobada por los matemáticos.[13][14][15][16][17][18] En el contexto de la teoría de cuerdas topológica, la simetría especular establece que dos teorías llamadas modelo A y modelo B son equivalentes en el sentido de que hay una dualidad que las relaciona.[19] Desde la postulación de su existencia, la simetría especular es un área activa de investigación en matemáticas, con el objetivo de desarrollar una formulación más completa y exacta de esta a partir del concepto físico.[20]

Círculos de Apolonio: Los ocho círculos de colores son tangentes a los tres círculos negros.

Muchas de las aplicaciones matemáticas importantes de la simetría especular pertenecen a la geometría enumerativa, una rama de las matemáticas. La geometría enumerativa se ocupa de contar el número de soluciones a las cuestiones geométricas, normalmente utilizando las técnicas de la geometría algebraica. Uno de sus primeros problemas fue planteado en torno al año 200 a. C. por el matemático griego Apolonio, quien se preguntó cuántos círculos son tangentes a tres circunferencias dadas en el plano. En general, la solución del problema de Apolonio es que hay ocho de tales círculos.[41]

El Clebsch cúbico

Los problemas enumerativos en matemáticas a menudo conciernen a una clase de objetos geométricos llamados variedades algebraicas, que se definen por la anulación de polinomios. Por ejemplo, el Clebsch cúbico ―ver la ilustración― se define mediante un polinomio de grado tres de cuatro variables. Los matemáticos del siglo xix Arthur Cayley y George Salmon llegaron al resultado de que hay exactamente 27 líneas rectas contenidas en su totalidad en esta superficie.[42]

Una generalización de ese problema consiste en determinar el número de líneas que se pueden trazar en una variedad de Calabi-Yau quíntica, como la que se ha ilustrado anteriormente, que está definida por un polinomio de grado cinco. El matemático alemán del siglo xix Hermann Schubert, calculó que hay exactamente 2875 de estas líneas. En 1986, el geómetra Sheldon Katz demostró que el número de curvas definidas por polinomios de grado dos que están contenidas en su totalidad en el quíntico es de 609 250.[41]

Para el año 1991, la mayoría de los problemas clásicos de la geometría enumerativa habían sido resueltos y el interés por la materia había comenzado a disminuir. Según el matemático Marcos Gross, «Como se habían resuelto los viejos problemas, la gente volvió a ponerse a verificar los números de Schubert con técnicas modernas, pero la cosa se estaba poniendo muy aburrida».[43] El campo se revitalizó en mayo de 1991 cuando los físicos Philip Candelas, Xenia de la Ossa, Pul Green y Linda Parkes mostraron que la simetría especular se podría utilizar para contar el número de curvas de grado tres en un quíntico de Calabi-Yau. Candelas y sus colaboradores calcularon que estas variedades de Calabi-Yau de seis dimensiones pueden contener exactamente 317 206 375 curvas de grado tres.[43]

Además del conteo de curvas de grado tres en una ecuación de quíntica triple, Candelas y sus colaboradores obtuvieron una serie de resultados más generales para contar curvas racionales que iban mucho más allá de las determinadas por los matemáticos.[44] Aunque los métodos utilizados en este trabajo se basaban en la intuición física, los matemáticos han conseguido demostrar algunas de las predicciones de la simetría especular, como las predicciones enumerativas.[32]

Además de sus aplicaciones en la geometría enumerativa, la simetría especular es una herramienta fundamental para hacer cálculos en la teoría de cuerdas. En el modelo A de la teoría de cuerdas topológica, varias cantidades de interés se expresan en términos de un conjunto infinito de números llamados invariantes Gromov-Witten, que son extremadamente difíciles de calcular. En el modelo B, los cálculos pueden reducirse a integrales clásicas y son mucho más fáciles.[45] Mediante la aplicación de la simetría especular, los teóricos pueden transformar las operaciones matemáticas complicadas del modelo A en los cálculos técnicamente más sencillos del modelo B, que dan como resultado las probabilidades de los diversos procesos físicos en la teoría de cuerdas. La simetría especular se puede combinar con otras dualidades para simplificar los cálculos en un modelo mediante su transformación en operaciones más simples en otro modelo relacionado con el primero por la dualidad y permite así obtener cantidades que son imposibles de estimar de otro modo.[46]

Más allá de la teoría de cuerdas, la simetría especular se utiliza para comprender aspectos de la teoría cuántica de campos, el formalismo que los físicos utilizan para describir partículas elementales. Por ejemplo, las teorías gauge son una clase de hipótesis físicas con un alto grado de simétricas que aparecen en el modelo estándar de la física de partículas y otras partes de la física teórica. Algunas teorías gauge que no forman parte del modelo estándar, pero que son importantes en la física de cuerdas por razones teóricas, la simetría especular es una herramienta computacional útil.[47] De hecho, la simetría especular se puede utilizar para realizar cálculos en una importante teoría gauge en cuatro dimensiones espacio-temporales estudiada por Nathan Seiberg y Edward Witten, y usada también en matemáticas en el contexto de los invariantes de Donaldson.[48] También hay una generalización de la simetría especular llamada simetría especular 3D que relaciona pares de teorías cuánticas de campo en tres dimensiones.[49]

Cuerdas abiertas conectadas a un par de D-branas

En la teoría de cuerdas, como en otras relacionadas en el ámbito de la física, una brana es un objeto físico que generaliza la noción de una partícula puntual a dimensiones superiores. Por ejemplo, una partícula puntual puede describirse como una brana de dimensión cero, mientras que una cuerda puede visualizarse como una brana de dimensión uno. También es posible considerar branas de dimensiones superiores. La palabra brana se deriva del término «membrana», que se refiere a una brana de dos dimensiones.[50]

En la teoría de cuerdas, una cuerda puede ser abierta, formando un segmento con dos puntos finales; o cerrada, formando un bucle cerrado. Cuando se estudian cuerdas abiertas, surgen las D-branas. A medida que una cuerda abierta se propaga a través del espacio-tiempo, es necesario que sus puntos finales se posicionen sobre una D-brana. La letra «D» en D-brana se asocia a la frontera de Dirichlet, que debe satisfacerse.[51]

Matemáticamente, las branas se pueden describir utilizando la noción de categoría,[52] una construcción matemática consistente en objetos, y para cualquier par de objetos, un conjunto de morfismos entre ellos. En la mayoría de los ejemplos, los objetos son estructuras matemáticas ―como conjuntos, espacios vectoriales o espacios topológicos― y los morfismos son funciones entre estas estructuras.[nb 8] También se pueden contemplar categorías donde los objetos son D-branas y los morfismos entre dos branas ${\displaystyle \alpha }$ y ${\displaystyle \beta }$ son estados de cuerdas abiertas estiradas entre ${\displaystyle \alpha }$ y ${\displaystyle \beta }$.[53]

En el modelo B de la teoría de cuerdas topológica, las D-branas son una subvariedad compleja del espacio de Calabi-Yau, junto con los datos adicionales que surgen de la existencia de cargas en los puntos extremos de las cuerdas.[53] Intuitivamente, una subvariedad puede considerarse como una superficie incrustada dentro de la variedad Calabi-Yau, aunque también pueden existir subvariedades de dimensiones diferentes a dos.[30] En lenguaje matemático, la categoría que cuenta con estas branas como sus objetos se conoce como la categoría derivada de haces coherentes de la variedad Calabi-Yau.[54] En el modelo A, las D-branas también se pueden contemplar como subvariedades de una variedad de Calabi-Yau. En términos generales, pertenecen a lo que los matemáticos conocen como subvariedades especiales de Lagrange.[54] Esto significa, entre otras cosas, que tienen la mitad de la dimensión del espacio en el que se asientan, y que minimizan la longitud, el área o el volumen.[55] La categoría que contiene estas branas y sus objetos se denomina categoría de Fukaya.[54]

La categoría derivada de haces coherentes se construye utilizando herramientas de la geometría compleja, una rama de las matemáticas que describe curvas geométricas en términos algebraicos y resuelve problemas geométricos utilizando ecuaciones algebraicas.[56] Por otra parte, la categoría de Fukaya se construye usando geometría simpléctica, una rama de las matemáticas que surgió de los estudios de la física clásica. La geometría simpléctica estudia espacios dotados con una forma simpléctica, una herramienta matemática que se puede utilizar para calcular el área en ejemplos bidimensionales.[19]

La conjetura de la simetría especular homológica de Maksim Kontsévich establece que la categoría derivada de haces coherentes en una variedad de Calabi-Yau equivale en cierto modo a la categoría Fukaya de su espejo.[57] Esta equivalencia proporciona una formulación matemática precisa de la simetría especular en la teoría de cuerdas topológica. Además, proporciona un puente inesperado entre dos ramas de la geometría, a saber, la geometría compleja y la geometría simpléctica.[58]

Un toro se puede ver como una unión de un número cuantitativamente indeterminado de círculos como el rojo en la imagen. Existe uno de esos círculos para cada punto en el círculo de color rosa.

En 1996, Andrew Strominger, Shing-Tung Yau, y Eric Zaslow sugirieron otro enfoque para comprender la simetría especular,[23] conocido posteriormente como la conjetura SYZ; el método consiste en dividir una variedad de Calabi-Yau en piezas más simples y transformarlas separadamente para conseguir la variedad de Calabi-Yau especular.[59]

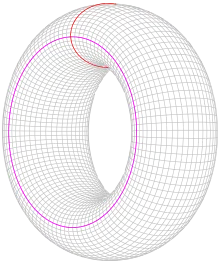
El ejemplo más simple de una variedad de Calabi-Yau es un toro de dos dimensiones[nb 2] o una figura con forma de rosquilla.[60] Considérese un círculo en esta superficie que pase una vez a través del agujero de la rosquilla, como el círculo rojo en la figura. Se pueden trazar infinitos círculos como este alrededor del toro; de hecho, toda la superficie es el resultado de la unión de esos círculos.[61] A continuación, se escoge un círculo auxiliar ${\displaystyle B}$ ―el círculo de color rosa en la figura― de tal manera que cada uno de los infinitos círculos en que se descompone el toro pase a través de un punto de ${\displaystyle B}$. Este círculo auxiliar parametriza los círculos de la descomposición, es decir, hay una correspondencia entre cada una de ellos y cada punto de ${\displaystyle B}$. El círculo ${\displaystyle B}$ es algo más que una lista, sin embargo, debido a que también determina cómo están dispuestos estos círculos en el toro. Este espacio auxiliar juega un papel importante en la conjetura SYZ.[55]

La idea de dividir un toro en círculos parametrizados por un espacio auxiliar se puede generalizar. Aumentando de dos a cuatro dimensiones reales, esta variedad Calabi-Yau se convierte en una superficie K3. Así como el toro se descompone en círculos, una superficie K3 de cuatro dimensiones se puede descomponer en toros bidimensionales. En este caso, el espacio ${\displaystyle B}$ es una esfera ordinaria. Cada punto de la esfera corresponde a uno de los toros de dos dimensiones, a excepción de veinticuatro puntos «malos» correspondientes a toros singulares.[55]

Las variedades de Calabi-Yau de interés principal en la teoría de cuerdas tienen seis dimensiones. Tales variedades se pueden dividir en 3-toros ―objetos definidos como la generalización de un toro en tres dimensiones― parametrizados por una 3-esfera ${\displaystyle B}$ ―una generalización tridimensional de una esfera―. Cada punto de ${\displaystyle B}$ corresponde a un 3-toro, a excepción de un número infinito de puntos «malos» que forman segmentos dispuestos en una cuadrícula sobre el espacio Calabi-Yau y que corresponden a toros singulares.[62]

Una vez que la variedad de Calabi-Yau ha sido descompuesta en partes más simples, la simetría especular se puede entender de una manera geométrica intuitiva. A modo de ejemplo, considérense el toro descrito anteriormente. Imagínese que este toro representa el «espacio-tiempo» de una teoría física. Los objetos fundamentales de esta hipótesis serán cuerdas que se propagan a través del espacio-tiempo de acuerdo a las reglas de la mecánica cuántica. Una de las dualidades básicas de la teoría de cuerdas es la dualidad T, que establece que una cuerda que se propaga alrededor de un círculo de radio ${\displaystyle R}$ es equivalente a una cuerda que se propaga alrededor de un círculo de radio ${\displaystyle 1/R}$ en el sentido de que todas las cantidades observables en una descripción se corresponden con otras en la descripción dual.[63] Por ejemplo, una cuerda tiene un momento, ya que se propaga alrededor de un círculo, y también puede dar vueltas alrededor de este una o más veces. El número de veces que la cuerda gira alrededor de un círculo se llama el índice. Si una cuerda tiene un momento ${\displaystyle p}$ y un índice ${\displaystyle n}$ en una descripción, tendrá el momento ${\displaystyle n}$ y el índice ${\displaystyle p}$ en la descripción dual.[63] Mediante la aplicación de la dualidad T simultáneamente a todos los círculos en que se descompone el toro, los radios de estos se invierten y queda un nuevo toro que es más «grueso» o «esbelto» que el original. Este toro es el espejo del Calabi-Yau original.[64]

La dualidad T se puede extender desde los círculos a los toros de dos dimensiones que aparecen en la descomposición de una superficie K3 o a los hipertoros tridimensionales que aparecen en la descomposición de una variedad de Calabi-Yau de seis dimensiones. En general, la conjetura SYZ afirma que la simetría especular es equivalente a la aplicación simultánea de la dualidad T a estos toros. En cada caso, el espacio ${\displaystyle B}$ proporciona una especie de modelo que describe cómo ensamblar estos en una variedad de Calabi-Yau.[65]

• Yau, Shing-Tung; Nadis, Steve (2010). The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions. Basic Books. ISBN 978-0-465-02023-2.
• Zaslow, Eric (2008). «Mirror Symmetry». En Gowers, Timothy, ed. The Princeton Companion to Mathematics. ISBN 978-0-691-11880-2.
• Zaslow, Eric (2005). «Physmatics». .

• Aspinwall, Paul; Bridgeland, Tom; Craw, Alastair; Douglas, Michael; Gross, Mark; Kapustin, Anton; Moore, Gregory; Segal, Graeme; Szendröi, Balázs; Wilson, P.M.H., eds. (2009). Dirichlet Branes and Mirror Symmetry. American Mathematical Society. ISBN 978-0-8218-3848-8.
• Cox, David; Katz, Sheldon (1999). Mirror symmetry and algebraic geometry. American Mathematical Society. ISBN 978-0-8218-2127-5.
• Hori, Kentaro; Katz, Sheldon; Klemm, Albrecht; Pandharipande, Rahul; Thomas, Richard; Vafa, Cumrun; Vakil, Ravi; Zaslow, Eric, eds. (2003). Mirror Symmetry. American Mathematical Society. ISBN 0-8218-2955-6.