Punto material

ㅤArtículo principal: Masa puntual

La masa puntual es el concepto, por ejemplo, en la física clásica, de un objeto físico (típicamente materia) que tiene una masa no nula y, sin embargo, es explícitamente (o se piensa o modela como) infinitesimal (infinitamente pequeño) en su volumen o dimensiones lineales. En la teoría de la gravedad, los objetos extendidos pueden comportarse como puntuales incluso en su proximidad inmediata. Por ejemplo, los objetos esféricos que interactúan en un espacio tridimensional y cuyas interacciones se describen mediante la gravitación newtoniana se comportan como si toda su materia estuviera concentrada en sus centros de masas^{[cita requerida]}. Esto es cierto para todos los campos descritos por una ley cuadrática inversa.[4][5]

ㅤArtículo principal: Carga puntual

Potencial escalar de una carga puntual poco después de salir de un imán dipolar, moviéndose de izquierda a derecha.

Al igual que en el caso de las masas puntuales, en el electromagnetismo los físicos hablan de una carga puntual, una partícula puntual con una carga distinta de cero.[6] La ecuación fundamental de la electrostática es la ley de Coulomb, que describe la fuerza eléctrica entre dos cargas puntuales. Otro resultado, el teorema de Earnshaw, afirma que una colección de cargas puntuales no puede mantenerse en una configuración de equilibrio únicamente por la interacción electrostática de las cargas. El campo eléctrico asociado a una carga puntual clásica aumenta hasta el infinito a medida que la distancia de la carga puntual disminuye hacia el cero, lo que sugiere que el modelo ya no es preciso en este límite.

Un protón combina dos cuarks arriba y un cuark abajo, mantenidos juntos por los gluones.

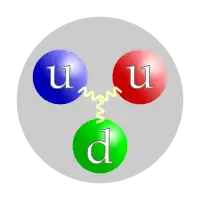
Existe una distinción entre una partícula elemental (también llamada partícula puntual) y una partícula compuesta en la mecánica cuántica. Una partícula elemental, como un electrón, un cuark o un fotón, es una partícula sin estructura interna conocida. Una partícula compuesta, como un protón o un neutrón, tiene una estructura interna (véase la figura). Sin embargo, ni las partículas elementales ni las compuestas están localizadas espacialmente debido al principio de incertidumbre de Heisenberg. El paquete de ondas de las partículas siempre ocupa un volumen distinto de cero. Por ejemplo, véase el orbital atómico: El electrón es una partícula elemental, pero sus estados cuánticos forman patrones tridimensionales.

Sin embargo, hay una buena razón por la que una partícula elemental suele llamarse partícula puntual. Aunque una partícula elemental tenga un paquete de ondas deslocalizado, el paquete de ondas puede representarse como una superposición cuántica de estados cuánticos en la que la partícula está precisamente localizada. Además, las interacciones de la partícula pueden representarse como una superposición de interacciones de estados individuales que están localizados. Esto no es cierto para una partícula compuesta, que nunca puede representarse como una superposición de estados cuánticos exactamente localizados. En este sentido, los físicos pueden hablar del «tamaño» intrínseco de una partícula: El tamaño de su estructura interna, no el tamaño de su paquete de ondas. El «tamaño» de una partícula elemental, en este sentido, es exactamente cero.

Por ejemplo, en el caso del electrón, las pruebas experimentales demuestran que el tamaño de un electrón es inferior a 10⁻¹⁸ m.[7] Esto es coherente con el valor esperado de exactamente cero. (Esto no debe confundirse con el radio clásico del electrón, que, a pesar del nombre, no está relacionado con el tamaño real de un electrón).

Una masa puntual en la teoría de la probabilidad no se refiere a la masa en el sentido de la física. Normalmente, un suceso individual (punto) en un espacio muestral continuo tiene una probabilidad nula. Y sólo los intervalos de sucesos tienen una probabilidad distinta de cero. Sin embargo, si un suceso individual tiene una probabilidad distinta de cero, se dice que es una masa puntual. Recibe este nombre por la analogía común entre el concepto de densidad de probabilidad y la densidad en el sentido de la física. Estos puntos también se denominan atómicos. Una medida de probabilidad con masas puntuales no es (por definición) continua para la medida de Lebesgue. Este comportamiento se manifiesta como un salto en la función de distribución acumulativa.

• Partícula de prueba
• Partícula elemental
• Grama
• Carga (física) (concepto general, no limitado a la carga eléctrica)
• Modelo estándar de la física de partículas
• Dualidad onda-partícula