Teoría del orden
La teoría del orden es una rama de la matemática que estudia varias clases de relaciones binarias que capturan la noción intuitiva del orden matemático. Este artículo provee una introducción detallada a este campo e incluye algunas de las definiciones básicas. Para una rápida búsqueda de un término orden teórico, hay también un glosario de teoría del orden. Una lista de asuntos sobre orden recoge los artículos que existen en relación con esta teoría del orden.
Trasfondo y motivación
El orden aparece por todas partes - por lo menos, si se trata de matemática y áreas relacionadas tales como la informática. El primer orden que uno típicamente encuentra en la educación matemática de la escuela primaria es el orden ≤ de los números naturales. Este concepto intuitivo es fácilmente extendido a otros conjuntos de números, tal como los enteros y reales. De hecho la idea de ser mayor o menor que otro número es una de las intuiciones básicas de los sistemas de numeración en general (que uno generalmente se interesa también en la diferencia real de dos números, que no viene dada por el orden). Otro ejemplo popular de un orden es el orden lexicográfico de las palabras en un diccionario.
Los tipos antedichos de orden tienen una propiedad especial: cada elemento se puede comparar con cualquier otro elemento, es decir es o mayor, o menor, o igual. Sin embargo, esto no siempre es un requisito deseable. Un ejemplo bien conocido es el orden de los subconjuntos de un conjunto. Si un conjunto contiene los elementos de cierto otro conjunto, entonces se puede decir que es mayor o igual. Con todo, hay conjuntos que pueden no ser comparables de este modo, puesto que cada uno puede contener algún elemento que no esté presente en el otro. Por lo tanto, inclusión de subconjuntos es un orden parcial, en comparación con los órdenes totales dados antes.
Alentadas por los amplios usos prácticos de los órdenes, se pueden definir numerosas clases especiales de conjuntos ordenados, algunas de las cuales han llegado a ser campos matemáticos por sí mismos. Además, la teoría del orden no se restringe a las varias clases de relaciones de orden, sino que también considera funciones apropiadas entre ellas. Un ejemplo simple de una propiedad orden teórica viene del análisis donde encontramos con frecuencia a las funciones monótonas.
Introducción a las definiciones básicas
Esta sección tiene como objetivo dar una primera guía al reino de los conjuntos ordenados. Está dirigida al lector que tiene un conocimiento básico teoría de conjuntos y aritmética y que sabe qué es una relación binaria, pero que no está familiarizado, hasta ahora, con consideraciones teóricas sobre orden.
Conjuntos parcialmente ordenados
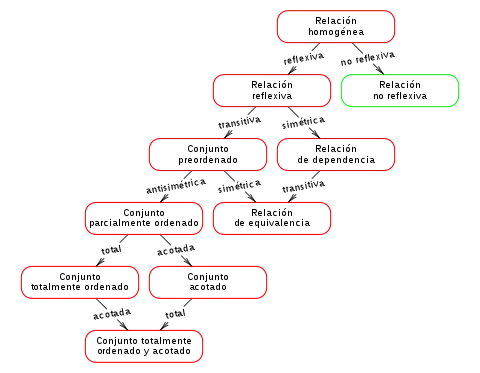
Como ya se hizo alusión arriba, un orden es una relación binaria especial. Por lo tanto consideremos algún conjunto P y una relación binaria ≤ en P. Entonces ≤ es un orden parcial si es reflexiva, antisimétrica, y transitiva, es decir, para todo a, b y c en P, tenemos que:
- a ≤ a (reflexividad)
- si a ≤ b y b ≤ c entonces a ≤ c (transitividad)
- si a ≤ b y b ≤ a entonces a = b, (antisimetría).
Un conjunto con un orden parcial se llama conjunto parcialmente ordenado, o, en breve, poset (del inglés partially ordered set). El término conjunto ordenado a veces también se utiliza para los posets, mientras esté claro del contexto que no se quiere significar ninguna otra clase de órdenes. Comprobando esta propiedad, se ve inmediatamente que los bien conocidos órdenes de los naturales, enteros, racionales y reales son todos órdenes en el antedicho sentido. Sin embargo, tienen la propiedad adicional de ser total, es decir, para todo a, b en X
- a ≤ b o b ≤ a (totalidad)
este orden se puede también llamar orden lineal o cadena. mientras que muchos órdenes clásicos son lineales, el orden entre subconjuntos de un conjunto proporciona un ejemplo donde este no es el caso. De hecho, muchas propiedades avanzadas de los posets son interesantes principalmente para un orden no lineal.
Visualizando órdenes
Antes de proceder con más ejemplos y definiciones, será provechoso poder exhibir un orden de una manera gráfica conveniente, para proporcionar un "cuadro" que uno pueda tener en mente (o en papel) cuando se intente acceder a conceptos más abstractos. Para este propósito se han introducidos los, así llamados, diagramas de Hasse. Estos son grafos donde los vértices son los elementos del poset y la relación de orden está indicada por las aristas y la posición relativa de los vértices. Los órdenes se dibujan de abajo hacia arriba: si un elemento x es menor que y entonces existe una trayectoria de x hasta y que se dirige hacia arriba. A menudo es necesario que la conexión entre puntos se intersequen, pero los puntos nunca deben ser situados en conexión directa entre otros dos puntos.
Aún los conjuntos infinitos pueden a veces ser ilustrados por diagramas similares, usando puntos suspensivos (...) después de dibujar un suborden finito que sea lo suficientemente instructivo. Esto funciona bien para los números naturales, pero falla para los reales, donde no existe el inmediato sucesor. Sin embargo, frecuentemente se obtiene una intuición relacionada con diagramas de este tipo.
Todos los órdenes antedichos son muy comunes en matemática, sin embargo hay también ejemplos que uno no considera a menudo como órdenes. Por ejemplo, la relación de identidad "=" en un conjunto es un orden parcial. Dentro de este orden, cualesquiera dos (i.e. distintos) elementos son incomparables. Es también la única relación que es un orden parcial y una relación de equivalencia. El diagrama de Hasse de tal orden discreto es solamente una colección de puntos etiquetados, sin ninguna arista entre ellos.
Otro ejemplo viene dado por la relación de divisibilidad "|". Para dos números naturales n y m, escribimos n|m si n divide a m sin resto. Uno ve fácilmente que esto da realmente un orden parcial. Un ejercicio instructivo es dibujar el diagrama de Hasse para el conjunto de los números naturales que son menores o iguales que, digamos, 13, ordenados por |.
Elementos especiales dentro de un orden
En un conjunto parcialmente ordenado hay algunos elementos que desempeñan un papel especial. El ejemplo más básico está dado por el mínimo de un poset. Por ejemplo, 1 es el mínimo de los números naturales y el conjunto vacío es el mínimo bajo el orden de subconjuntos. Formalmente, esto se puede describir por la propiedad:
- 0 ≤ a, para todo elemento a del conjunto ordenado.
Es frecuente encontrar la notación 0 para el mínimo, incluso cuando no se refiera a números. Sin embargo, en un orden de un conjunto numérico, esta notación puede ser inadecuada o ambigua, puesto que el número 0 no siempre es el mínimo. Un ejemplo es el antedicho orden de divisibilidad |, donde 1 es el mínimo puesto que divide a todo el resto de números. Por otra parte, 0 es un número que se divide por todo el resto de números. ¡Por lo tanto es el máximo del orden! Otros términos frecuentes para estos elementos son fondo y tapa o cero y uno. Pueden no existir los elementos "mínimo" o "máximo", como demuestra el ejemplo de los números reales. Por otra parte, si existen son siempre únicos. En contraste, consideremos la relación de divisibilidad | en el conjunto {2, 3, 4, 5, 6}. Aunque este conjunto no tiene ni tapa ni fondo, los elementos 2, 3, y 5 no tienen ningún elemento debajo, mientras que 4, 5, y 6 no tienen ninguno otro número arriba. Tales elementos se llaman minimales y maximales, respectivamente. Formalmente, un elemento m es minimal si:
- a ≤ m implica a = m, para todo elemento a.
Intercambiando ≤ con ≥ obtenemos la definición de maximal. Como el ejemplo demuestra, puede haber muchos elementos minimales o maximales y algún elemento puede ser maximal y minimal (e.g. 5 arriba). Sin embargo, si hay un elemento mínimo, entonces es el único elemento minimal del orden. (Si se sigue estrictamente la definición dada. Lamentablemente hay una tradición matemática "a contrario": considerar los minimales y maximales en el conjunto despojado de su máximo y su mínimo, si los hubiere. Esto debe recordarse. N.T.). Una vez más, en los posets no siempre hay infinitos elementos maximales - el conjunto de todos los subconjuntos finitos en un conjunto infinito dado, ordenado por inclusión de subconjuntos, proporciona uno, entre muchos, contraejemplo. Una herramienta importante para asegurar la existencia de elementos maximales bajo ciertas condiciones es el Lema de Zorn.
Los subconjuntos de un conjunto parcialmente ordenado heredan el orden. Ya aplicamos esto al considerar el subconjunto {2, 3, 4, 5, 6} de los números naturales con el orden de divisibilidad inducido. Hay también elementos de un poset que son especiales con respecto a cierto subconjunto del orden. Esto conduce a la definición de cota superior. Dado un subconjunto S de cierto poset P, una cota superior de S es un elemento b de P que está sobre todo elemento de S. Formalmente, esto significa que
- s ≤ b, para todo s en S.
Cota inferior se define invirtiendo el orden. Por ejemplo, -5 es una cota inferior de los números naturales como subconjunto de los enteros. Dado un conjunto de conjuntos , una cota superior para éstos conjuntos viene dado por su unión. De hecho, esta cota superior es muy especial: es el más pequeño conjunto que contiene todos los conjuntos dados. Por lo tanto, encontramos la menor cota superior de un conjunto de conjuntos. Este concepto se llama también supremo y para un conjunto S se escribe sup S o VS para su menor cota superior. Inversamente, la mayor cota inferior se la conoce como ínfimo y se denota inf S o ^S. Este concepto desempeña un papel importante en muchos usos de la teoría del orden. Para dos elementos x y y, uno también escribe x v y y x ^ y para sup{x, y} e inf{x, y}, respectivamente.
Usando Wikipedia TeX markup, uno puede también escribir y , así como símbolos grandes y . Observe, sin embargo, que todos esos símbolos pueden no tener símbolo de tamaño correspondiente al de la fuente del texto estándar y, por tanto, se prefiere utilizarlos en líneas adicionales. Muchos de los navegadores de hoy son incapaces de representar ∨ para v y ∧ para ^ en algunas plataformas, y por lo tanto se evita aquí.
Considere otro ejemplo en la relación | para los números naturales. La menor cota superior de dos números es el menor número que es múltiplo de ambos, es decir el mínimo común múltiplo. Mayor cota inferior es, alternativamente, el máximo común divisor.
Dualidad
En las anteriores definiciones, a menudo, observamos que un concepto puede ser definido por invertir simplemente el orden en una definición anterior. Este es el caso para "menor" y "mayor", para "mínimo" y "máximo", para "cota superior " y "cota inferior", etcétera. Esto es una situación general en teoría de orden: Un orden dado se puede invertir con solamente intercambiar su dirección, pictóricamente dar vuelta el diagrama de Hasse de arriba para abajo. Esto da el, así llamado, orden dual, inverso u opuesto.
Cada definición orden teórica tiene su dual: es la noción que se obtiene al aplicar la definición al orden inverso. Dada la simetría de todos los conceptos, esta operación preserva los teoremas del orden parcial. Para un resultado matemático dado, se puede, simplemente, invertir el orden y substituir todo definición por su dual y obtener otro teorema válido. Esto es importante y útil, puesto que uno obtiene dos teoremas al precio de uno. Más detalle y ejemplos se pueden encontrar en el artículo sobre dualidad en teoría de orden.
Construcción nuevos órdenes
Hay muchas maneras de construir órdenes o de combinar órdenes en uno nuevo. El orden dual es un primer ejemplo. Otra construcción importante es el producto cartesiano de dos conjuntos parcialmente ordenados, junto con el orden producto en pares de elementos. Esto se define por los órdenes originales haciendo (a, x) ≤ (b, y) si a ≤ b y x ≤ y. La unión disjunta de dos conjuntos parcialmente ordenados es otra construcción típica, donde el orden es exactamente la unión de los órdenes originales.
Como en el caso del orden usual de números, cada orden parcial ≤ da lugar a un orden estricto <, al definir a < b si a ≤ b y no b ≤ a. Esta transformación puede ser invertida haciendo a ≤ b si a < b o a = b.
Funciones entre órdenes
Es razonable requerir que las funciones entre conjuntos parcialmente ordenados tengan ciertas propiedades adicionales, que se relacionen con la relación de orden de los dos conjuntos. La condición más fundamental que se presenta en este contexto es la monotonía. Un función f de un poset P a un poset Q es monótona u orden preservante, si a ≤ b en P implica f(a) ≤ f(b) en Q. La conversa de esta implicación conduce a una función que es orden reflectante, es decir una función f como arriba para la cual f(a) ≤ f(b) implica a ≤ b. Por otra parte, una función puede también ser orden inversora o antítona, si a ≤ b implica f(a) ≥ f(b).
Una inmersión de orden es una función f entre órdenes que es orden preservante y orden reflectante. Ejemplos para esta definición se encuentran fácilmente. Por ejemplo, función que mapea un número natural en su sucesor es claramente monótona con respecto al orden natural. Cualquier función de un orden discreto, es decir un conjunto ordenado por el orden identidad "=", es también monótono. Mapear cada número natural al correspondiente número real da un ejemplo para una inmersión de orden. El complemento conjuntista en un conjunto de partes es un ejemplo de una función antítona.
Una importante pregunta es cuándo dos órdenes son "esencialmente iguales", es decir cuándo son lo mismo salvo retitular elementos. Un isomorfismo de orden es una función que define tal renombrar. Un isomorfismo de orden es una función monótona biyectiva que tiene una inversa monótona. Esto es equivalente a una inmersión de orden sobreyectiva. Por lo tanto, la imagen f(P) de una inmersión de orden es siempre isomorfa a P, lo que justifica el término "inmersión".
Un más elaborado tipo de función es la, así llamada, conexión de Galois. Conexiones de Galois monótonas pueden ser vistas como una generalización de los isomorfismos de orden, puesto que están constituidas por dos funciones en inversa dirección, que no son inversas absolutas una de la otra, pero tienen cercana relación.
Otro tipo especial de endofunción en un poset es el operador de clausura, que no solamente es monotónico, sino también idempotente, es decir. f(x) = f(f(x)), y extensivo, es decir. x ≤ f(x). este tiene mucho uso en todo clase de "clausuras" que aparecen en matemática.
Además de compatible con la mera relación de orden, una función entre posets puede también comportarse bien con respecto a elementos especiales y construcciones. Por ejemplo, cuando se habla de posets con menor elemento, parece razonable considerar solamente una función monotónica que preserve este elemento, es decir que mapee menor elemento en menor elemento. Si el ínfimo binario ^ existe, entonces una propiedad razonable puede ser requerir que f(x^y) = f(x) ^ f(y), para todo x y y. Todas estas propiedades, y de hecho muchas más, pueden ser agrupadas bajo la etiqueta función que preserva límite.
Finalmente, uno puede invertir la visión, cambiar funciones de orden a orden de funciones. De hecho, las funciones entre dos posets P y Q pueden ser ordenadas vía el orden punto a punto. Para dos funciones f y g, se tiene f ≤ g si f(x) ≤ g(x) para todo elemento x en P. Esto ocurrirá por ejemplo en teoría de dominios, donde los espacios funcionales desempeñan un importante papel.
Tipos especiales de orden
Muchas de las estructuras que son estudiadas en teoría de orden emplean relaciones con propiedades adicionales. De hecho, algunas relaciones que no son de orden parcial son de especial interés. Principalmente, el concepto de preorden tiene que ser mencionado. Un preorden es una relación que es reflexiva y transitiva, pero no necesariamente antisimétrica. Cada preorden induce una relación de equivalencia entre elementos, donde a es equivalente a b, si a ≤ b y a ≥ b. Los preórdenes pueden ser convertidos en órdenes identificando todo elemento equivalente con respecto a esta relación.
Tipos básicos de órdenes especiales ya se dieron en forma de orden total. Una simple pero útil propiedad adicional conduce al, así llamado, buen orden, dentro del que todo subconjunto no vacío tiene un menor elemento (también denominado primer elemento). Muchos otros tipos de orden se presentan cuando se garantiza la existencia de ínfimos y supremos de ciertos conjuntos. Centrándose en este aspecto, generalmente referido como completitud de órdenes, se obtiene:
- Posets acotados, es decir posets con menor y mayor elementos (que son precisamente supremo e ínfimo del conjunto vacío),
- reticulados, en que cada conjunto finito no vacío tiene supremo e ínfimo,
- reticulados completos, donde cada conjunto tiene supremo e ínfimo, y
- órdenes parciales dirigidos completos (dcpos), que garantizan la existencia de supremo en todo subconjunto dirigido y son estudiados en teoría de dominios.
Sin embargo, uno puede ir incluso más allá: si todo ínfimo finito no vacío existe, entonces ^ puede ser visto como una operación binaria total en el sentido del álgebra universal. Por lo tanto, en un reticulado, dos operaciones ^ y v están disponibles, y se puede definir nuevas propiedades dando identidades, tal como
- x ^ (y v z) = (x ^ y) v (x ^ z), para todo x, y, y z.
Este condición se llama distributividad y dar lugar a los reticulados distributivos. Hay algunas otras importantes leyes de distributividad que son discutidas en el artículo sobre la distributividad en teorías de orden. Algunas estructuras de orden adicionales que son a menudo especificadas vía operación algebraica y definiendo identidades son
en que ambas introducen una nueva operación ~ llamada negación. Ambas estructuras desempeñan un papel en lógica matemática y especialmente las álgebras de Boole tienen importante uso en informática. Finalmente, varias estructuras en matemática combinan orden con operaciones aún más algebraicas, como el caso de quantales, que permite la definición de una operación de adición.
Existen muchas otras importantes propiedades de los posets. Por ejemplo, un poset es localmente finito si cada intervalo cerrado [a, b] en él es finito. Los posets localmente finitos dan lugar a álgebras de incidencia que alternadamente pueden ser utilizadas para definir característica de Euler de posets finitos acotados.
Subconjuntos de conjuntos ordenados
En un conjunto ordenado, uno puede definir muchos tipos especiales de subconjuntos basados en el orden dado. Un ejemplo simple son los conjuntos superiores, es decir conjuntos que contienen todo elemento que esté sobre ellos en el orden. Formalmente, la clausura superior de un conjunto S en un poset P viene dado por el conjunto {x en P| hay algún y en S con y ≤ x}. Un conjunto que es igual a su clausura superior se llama un conjunto superior. conjunto inferior es definido dualmente.
Subconjuntos inferiores más complicados son los ideales, que tienen la propiedad adicional que cada dos de sus elementos tiene cota superior dentro del ideal. Su noción dual son los filtros. Un concepto relacionado es el de subconjunto dirigido, que como un ideal contiene cota superior de un subconjunto finito, pero no tiene por qué ser un conjunto inferior. Además, a menudo se generaliza a conjuntos preordenados.
Un subconjunto que es - como sub-poset - linealmente ordenado, se llama una cadena. La noción opuesta, anticadena, es un subconjunto que no contiene ningún par de elementos comparables, es decir que es un orden discreto.
Áreas matemáticas relacionadas
Aunque la mayoría de las áreas matemáticas usan orden de uno u otra manera, también hay algunas teorías que tienen una relación que va mucho más allá de la mera utilización. Junto con su importante punto de contacto con la teoría de orden, algunas serán presentadas abajo.
Álgebra universal
Según lo ya mencionado, los métodos y el formalismo del álgebra universal son una herramienta importante para muchas consideraciones orden teóricas. Aparte de formalizar órdenes en términos de estructuras algebraicas que satisfacen ciertas identidades, se pueden también establecer otras conexiones con el álgebra. Un ejemplo es la correspondencia entre las álgebras de Boole y los anillos de Boole. Otros aspectos tienen que ver con la existencia de construcciones libres, tal como los reticulados libres basados en un conjunto de generadores. Además, los operadores de clausura son importantes en el estudio del álgebra universal.
Topología
En topología el orden desempeña un muy prominente papel. De hecho, el conjunto de los abiertos proporciona un clásico ejemplo de un reticulado completo, más exactamente un álgebra de Heyting completa (o "marco" o "locale"). Los filtros y las redes son nociones relacionadas con la teoría de orden y el operador clausura conjuntista puede ser utilizado para definir una topología. Más allá de esta relación, la topología se puede mirar únicamente en términos del reticulado de conjuntos abiertos, que conduce al estudio de la topología sin puntos. Además, un preorden natural de elementos del conjunto subyacente de una topología viene dada por el, así llamado, orden de especialización, que es realmente un orden parcial si la topología es T0.
Inversamente, en teoría de orden, uno a menudo hace uso de resultados topológicos. Hay varias maneras de definir subconjuntos de un orden que pueden ser considerados como conjunto abiertos de una topología. Especialmente, es interesante considerar topologías en un poset (X, ≤) que reobtiene ≤ como su orden de especialización. La más fina de tales topologías es la topología de Alexandrov, dada al tomar todos los conjuntos superiores ("upper") como abiertos. Inversamente, la más gruesa topología que induce el orden de especialización es la topología superior, que tiene los complementos de los ideales principales (es decir conjuntos de la forma { y en X|y ≤ x} para cada x) como una subbase. Adicionalmente, una topología con orden de especialización ≤ puede ser orden consistente, significando que sus conjuntos abiertos son "inaccesibles por supremos dirigidos" (con respecto ≤). La topología más fina de un orden consistente es la topología de Scott, que es más gruesa que la topología de Alexandrov. Una tercera topología importante en esta línea es la topología de Lawson. Hay cercanas conexiones entre estas topologías y los conceptos de la teoría de orden. Por ejemplo, una función preserva supremos dirigidos si y sólo si es continuo con respecto a la topología de Scott (por este razón esta propiedad orden teórica es también llamada continuidad de Scott).
Teoría de categorías
La visualización de órdenes con diagramas de Hasse tiene una generalización directa: en vez exhibir elemento menores bajo los mayores, la dirección del orden se puede también representar dando la dirección de las aristas del grafo. De esta manera, cada orden se ve como equivalente a un grafo dirigido acíclico, donde los nodos son los elementos del poset y hay una trayectoria dirigida de a a b si y solamente si a ≤ b. Eliminando el requisito acíclico, uno puede también obtener todos los preórdenes.
Cuando es equipado con todas las aristas transitivas, estos grafos son solamente categorías especiales, donde los elementos son los objetos y cada conjunto de morfismos entre dos elementos es a lo sumo un singletón. Funciones entre órdenes se convierten en funtores entre categorías. Interesantemente, muchas ideas de la teoría de orden son simplemente pequeñas versiones de los conceptos de la teoría de las categorías. Por ejemplo, un ínfimo es precisamente un producto categórico. Más en general, uno puede subsumir supremos e ínfimos bajo la noción abstracta de un límite categórico (o colímite, respectivamente). Otro lugar en donde las ideas categoriales surgen es el concepto de una conexión de Galois (monótona), que es precisamente igual a un par de funtores adjuntos.
Pero la teoría de las categorías también tiene un impacto en la teoría de orden de mayor escala. Clases de posets con funciones apropiadas según lo discutido arriba forman interesantes categorías. A menudo uno puede también establecer construcción de órdenes, como el orden producto, en término de categoría. Otras intuiciones resultan cuando categorías de orden resultan equivalentes categóricas a otra categoría, por ejemplo de espacios topológicos. Este línea de investigación conduce a varios teoremas de representación, a menudo recogidos bajo la etiqueta dualidad de Stone.
Esquema de temas relacionados
Referencias
- Gierz, G., K. H. Hofmann, K. Keimel, J. D. Lawson, M. Mislove y D. S. Scott, «Continuous Lattices and Domains.» En Encyclopedia of Mathematics and its Applications, Vol. 93, Cambridge University Press, 2003. ISBN 0-521-80338-1