Toro complejo

En matemáticas, un toro complejo es un tipo particular de variedad compleja M cuya variedad diferenciable subyacente es un toro en el sentido habitual (es decir, el producto cartesiano de algún número N de circunferencias). Aquí N debe ser el número par 2n, donde n es la dimensión compleja de M.

El toro complejo asociado a una retícula que abarca dos períodos, ω₁ y ω₂. Se identifican los bordes correspondientes

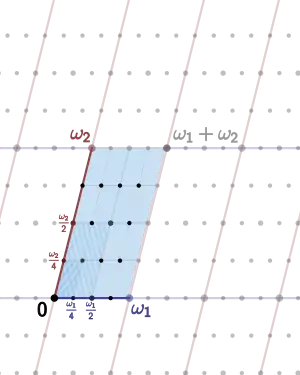
Todas estas estructuras complejas se pueden obtener de la siguiente manera: tómese una red Λ en Cⁿ considerada como espacio vectorial real; entonces el grupo cociente

Cⁿ/Λ

es una variedad compleja compacta. Todos los toros complejos, hasta el isomorfismo, se obtienen de esta manera. Para n = 1, esta es la construcción reticular del período clásico de las curvas elípticas. Para n > 1, Bernhard Riemann encontró las condiciones necesarias y suficientes para que un toro complejo sea una variedad algebraica; los que son variedades pueden integrarse en un espacio proyectivo complejo, y son las variedades abelianas.

Las incorporaciones proyectivas reales son complicadas (véase ecuaciones que definen variedades abelianas) cuando n > 1, y son realmente coextensivas con la teoría de las funciones theta de varias variables complejas (con módulo fijo). No hay nada tan simple como la descripción de la curva cúbica para n = 1. El álgebra computacional puede manejar casos pequeños razonablemente bien. Según el teorema de Chow, ningún toro complejo aparte de las variedades abelianas puede 'encajar' en el espacio proyectivo.