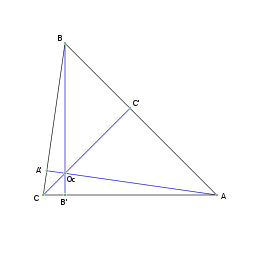
Triángulo escaleno
Un triángulo escaleno es la forma más general de triángulo, de ahí que las consideraciones que sobre este tipo de triángulos se puedan hacer son las que sobre triángulos en general se pueden hacer.

Un triángulo es un polígono cerrado de tres segmentos, cada uno de estos segmentos que forman el polígono es un lado del triángulo, y el punto donde se cortas dos lados es un vértice.
Los vértices se nombran con una letra mayúscula en sentido contrario a las agujas del reloj: A, B, C. Los lados se nombran con una letra minúscula igual a la del vértice opuesto: a, b, c. Los ángulos se nombran con una letra griega en el mismo orden que sus
vértices:
Los lados se pueden denominar por los dos vértices que lo delimitan:
Los ángulos se pueden nombrar también por la letra del vértice:
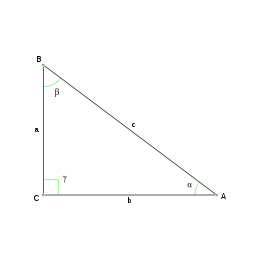
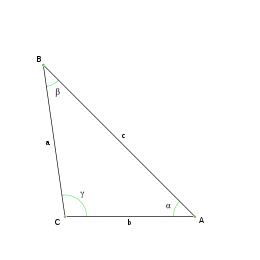
Un triángulo escaleno puede ser acutángulo, rectángulo u obtusángulo según sus ángulos.
 |
 |
 |
Puntos de un triángulo
Podemos ver algunos puntos característicos de un triángulo escaleno.
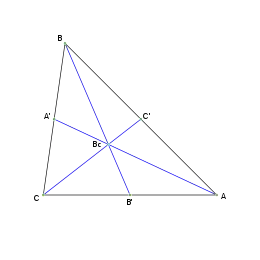
Baricentro
El baricentro: Bc, de un triángulo es el punto de corte de sus tres medianas. El baricentro es el centro de gravedad del triángulo.
 |
 |
 |
Circuncentro
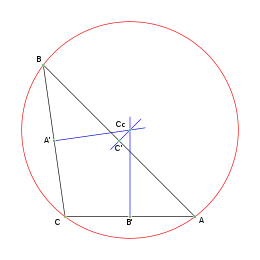
El circuncentro: Cc, de un triángulo es el punto donde se cortan las tres mediatrices del triángulo.[1][2][3][4][5] El circuncentro es el centro de la circunferencia que pasa por los tres vértices
 |
 |
 |
Incentro
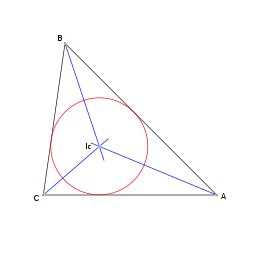
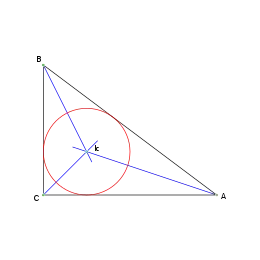
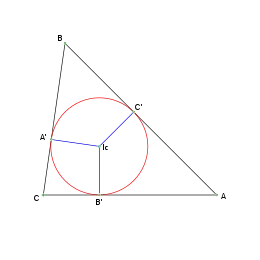
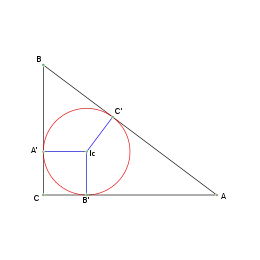
El incentro: Ic de un triángulo es el punto en el que se cortan las tres bisectrices de sus ángulos internos. Equidista de los tres lados, y por lo tanto, es el centro de la circunferencia inscrita en el triángulo, tangente a sus tres lados.
 |
 |
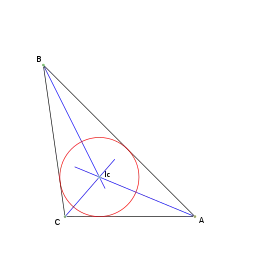 |
La recta que pasa por el incentro y es perpendicular a cada uno de los lados, corta al lado en el punto de tangencia de la circunferencia con el lado.
 |
 |
 |
Circunferencia circunscrita e inscrita
Como ya se ha mencionado todo triángulo tiene una circunferencia circunscrita y otra inscrita
 |
 |
 |
Recta de Euler
La recta de Euler, de un triángulo, es la recta que contiene el ortocentro, baricentro y circuncentro del triángulo.
 |
 |
 |
Teorema de los senos
dado un triángulo ABC, las medidas de los lados opuestos a los vértices: A, B y C son respectivamente: a, b, c, y sus ángulos: entonces:
 |
 |
 |
Teorema del coseno
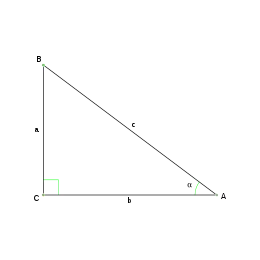
Dado un triángulo ABC cualquiera, siendo α, β, γ, los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:
 |
 |
 |
Teorema de la tangente
Siendo:a y b dos lados de un triángulo, y α y β los ángulos opuestos a estos dos lados. El teorema de la tangente establece que:
 |
 |
 |
Véase también
Enlaces externos
Bibliografía
- Álvarez, Emiliano (2003). Elementos de geometría. Universidad De Medellin. p. 594. ISBN 958-696-128-1.
- Stanley R. Clemens; Thomas J. Cooney (1998). Geometría. Pearson Educación.
- Núñez Cabello, Raúl. Geometría: el triangulo y la circunferencia. Publicatuslibros.com. p. 32.
Referencias
- Weisstein, Eric W. «Circumcenter». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Circumcircle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Simmons, Bruce (2011). «Circumcenter». Mathwords (en inglés). Consultado el 20 de febrero de 2012.
- Coxeter, Harold Scott MacDonald; Greitzer, Samuel L. (1972). Geometry Revisited. ISBN 0-88385-619-0.
- Puig Adam, Pedro (1972). Curso de Geometría Métrica.