Aberration géométrique

Les trois foyers principaux

L'aberration sphérique désigne une aberration dont l'une des conséquences est la disparition du foyer. Les rayons provenant du bord et du centre de l'optique ne se focalisent plus au même point. On observe alors une caustique de focalisation, dans laquelle le point image attendu sera remplacé par une surface plus ou moins floue. On définit trois foyers principalement :

• le foyer paraxial : il est défini par l'approximation de l'optique géométrique ;
• le meilleur foyer : il correspond à l'endroit où la tâche est la moins diffuse ;
• le foyer marginal : c'est celui correspondant à l'intersection des rayons marginaux (i.e. ceux qui passent par les bords de la pupille du système optique).

Les rayons parallèles ne se concentrent pas en un point unique

Pour une lentille sphérique, les rayons se trouvant au bord de la lentille focalisent à une place légèrement différente des rayons se trouvant au centre : l'image d'un point est donc une tache floue.

Ceci est dû au fait qu'une surface sphérique n'est pas la forme idéale pour réaliser une lentille. Il s'agit cependant de la forme la plus simple à polir, et elle reste très souvent utilisée.

L'aberration sphérique peut être minimisée en choisissant soigneusement une courbure particulière de la surface de la lentille : on utilise des lentilles non-sphériques que l'on nomme lentilles asphériques.

Dans l'animation ci-dessous, les rayons émergents sont construits en respectant rigoureusement la réfraction en I et J et l'on voit que le foyer se déplace. Pour obtenir un foyer là où il est indiqué dans les schémas plus haut il faut en pratique utiliser un diaphragme pour être dans les conditions de Gauss, ou conditions du stigmatisme approché.

Foyers d'une lentille convergente

Avec une ouverture faible, l'aberration de sphéricité disparaît. Cliquer sur l'image pour agrandir.

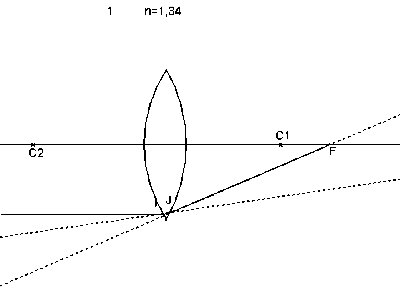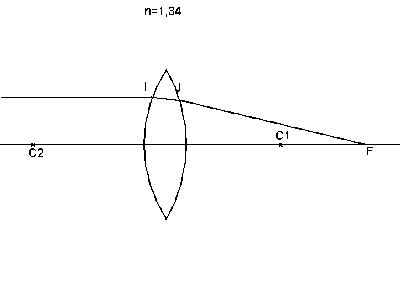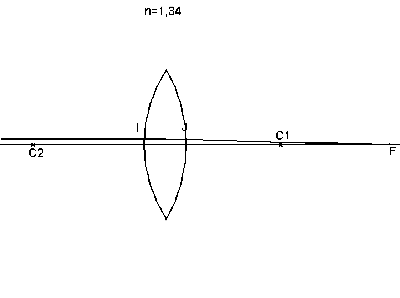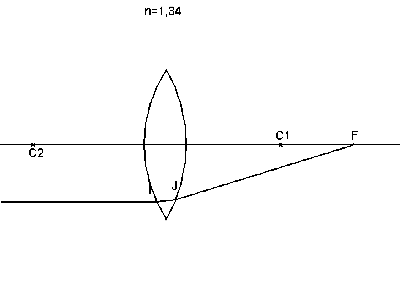
En photographie, l'aberration sphérique se manifeste par une perte de définition dans les zones à fort contraste.

Une lentille ou encore un prisme decomposera un faisceau de lumière blanche en plusieurs couleurs du spectre lumineux. Mais la réfraction de rayons lumineux de diverses couleurs ne se fait pas de la même manière. On verra donc des images à des endroits différents sur la projection. Ainsi, le point focal où se trouve l'image réfléchie par les rayons bleus sera le plus proche de l'image formé par les rayons rouges. La totalité de l'image formée par une lentille avec ce type de défaut est donc marquée de ce que l'on appelle une aberration chromatique.

Comparaison : même sujet, avec aberration chromatique sur la photo prise avec un objectif grand angulaire.

La seule chose à faire dans ce cas c'est de compenser cette aberration sur une lentille positive en lui ajoutant une lentille négative qui aura le même défaut mais opposé. On parlera alors d'objectif achromatique ou apochromatique[2].

L'aberration de coma désigne une aberration qui dépend du champ d'une part et de l'ouverture d'autre part (i.e. de la distance du point d'impact des rayons sur la pupille par rapport au centre de celle-ci). Cette aberration est dite « de champ » car elle n'existe pas sur l'axe optique. L'effet de cette aberration est de produire une tache en forme de comète dans un plan d'observation :

Les rayons parallèles qui ne sont pas dans l'axe optique de la lentille ne convergent pas tous en un même point sur le plan focal. Les rayons qui passent sur les bords de la lentille peuvent être focalisés plus loin ou plus près de l'axe optique que ceux passant au centre de la lentille. On parle respectivement de coma positive et de coma négative.

Aberration de coma

Comme pour l'aberration de sphéricité, il est possible de réduire la coma en choisissant une courbure particulière de la lentille. C'est le cas en astronomie avec les télescopes Ritchey-Chrétien dont les miroirs primaires et secondaires sont hyperboliques.

Une lentille optique présente à priori une symétrie axiale. Dans la pratique, cette symétrie n'est pas parfaite.

On constate alors, lors d'essais sur banc FTM ou d'impression sur film, que la distance focale de l'objectif n'est pas constante autour de l'axe optique. En effet, la distance focale dépend de l'indice de réfraction de la lentille et de son rayon de courbure. Dès lors que celui-ci n'est pas parfaitement homogène, la distance focale ne l'est pas non plus. On constate en particulier cet effet lors de l'impression de mire de Foucault disposant de traits horizontaux, verticaux, tangentiels et sagittaux. Ces traits ne présentent alors pas la même définition dans le plan de mise au point selon la direction des traits.

Une lentille est dite corrigée des défauts d'astigmatisme dès lors que son rayon de courbure a été homogénéisé le plus possible, mais des défauts résiduels sont pratiquement inévitables. Les objectifs corrigés de l'astigmatisme sont dits « anastigmat ».

Les objectifs modernes, calculés et fabriqués selon des procédés de haute précision (laser) sont quasiment exempts d'astigmatisme.

Les logiciels de calculs optiques tels que Zemax, Oslo ou encore Code V permettent de calculer les aberrations d'un système optique à partir d'un catalogue de lentilles classiques.

En effet, la correction des aberrations s'effectue par l'utilisation de plusieurs lentilles ayant des défauts qui se compensent. Un peu comme l'œil et les lunettes de vue[3].