Accord (musique)

Jusqu'à la Renaissance, les superpositions de plusieurs notes ne sont pas considérées comme des accords. L'écriture musicale est régie exclusivement par des règles de superpositions de notes et de lignes mélodiques, celles qui formeront le procédé d'écriture appelé contrepoint. Cependant, dès la fin du XIV^e siècle, une plus grande attention est accordée aux superpositions de trois notes consonantes entre elles, désignées aujourd'hui par les intervalles qui les séparent : tierce et quinte, tierce et sixte, quarte et sixtes (d'autres combinaisons, comme tierce et octave ou quinte et octave, elles aussi consonantes et fréquentes aux périodes précédentes, ne donnent cependant que deux notes différentes, si on admet que les deux notes à l'octave l'une de l'autre sont conceptuellement la même note).

Le goût croissant pour la sonorité pleine des superpositions de trois notes consonantes est probablement à l'origine de la notion d'accord. Les sonorités de ce type sont très recherchées au XVI^e siècle et parmi elles, en particulier, la combinaison tierce et quinte. Certaines compositions de la seconde moitié du XVI^e siècle, chez Lassus notamment, se composent presque exclusivement de ce type de sonorités.

Les trois états de l'accord de do majeur (do - mi - sol) :
• état fondamental ;
• premier renversement (accord de tierce et sixte) ;
• deuxième renversement (accord de quarte et sixte).

L'apparition de la basse continue à la fin du XVI^e siècle, cette méthode d'accompagnement qui consistait à empiler des consonances (et dans certains cas des dissonances) au-dessus de la partie de basse, favorise la prise de conscience des combinaisons consonantes comme des « blocs » du jeu de construction que constitue la composition. En outre, on prend conscience que les trois combinaisons consonantes, tierce et quinte, tierce et sixte, quarte et sixte, peuvent être considérées comme des « renversements » les unes des autres : Johannes Lippius, en particulier, dans plusieurs traités publiés vers 1610[4], explique que la tierce et sixte ainsi que la quarte et sixte peuvent être considérées comme des renversements de la tierce et quinte par déplacement de la basse au-dessus des autres voix : do-mi-sol, tierce et quinte, par exemple, peut devenir la tierce et sixte mi-sol-do par déplacement de la basse (do) d'une octave vers le haut ; et la même combinaison peut devenir la quarte et sixte sol-do-mi par un second déplacement, celle fois de la tierce originelle (mi) par-dessus les autres voix. L'idée de ces renversements a sa source dans les descriptions de contrepoints renversables, c'est-à-dire de superpositions de lignes interchangeables entre elles, où une ligne plus grave qu'une autre à un moment donné peut devenir plus aiguë que l'autre à un autre moment, par un simple déplacement vers l'octave.

La notion de renversement permet de concevoir la triade comme une entité abstraite, pouvant se présenter sous l'une ou l'autre de ses formes, qui sont trois formes possibles d'un même accord. Lippius appelle radix (« racine ») la note la plus grave de la combinaison tierce et quinte, dite aussi basis (« base ») de l'accord, quelle que soit par ailleurs la position dans laquelle l'accord se présente en réalité : que ce soit do-mi-sol, mi-sol-do ou sol-do-mi, par exemple, do est toujours considéré comme la « base » et l'accord est considéré comme un « accord de do ».

À partir de ce moment, les règles du contrepoint qui régissaient la superposition de lignes mélodiques tendent à se compléter de règles concernant la succession des accords. On en vient progressivement à considérer que les accords peuvent être décrits par la note de basse de leur position « fondamentale » (position de tierce et quinte), et cette considération ouvre la voie à la création d'une discipline nouvelle, celle de l'harmonie.

Accords principaux au piano

Les accords se construisent essentiellement à partir d'intervalles consonants. La description des consonances est d'abord arithmétique. Elle a été proposée par Pythagore dès le V^e siècle avant notre ère. Il a montré qu'en plaçant le chevalet mobile du monocorde au tiers de la longueur de la corde, les parties de part et d'autre, dans le rapport 2/1, sonnaient l'octave ; de même le chevalet aux deux cinquièmes de la longueur permettait de comparer deux parties dans le rapport 3/2, sonnant la quinte; et le chevalet aux trois septièmes permettait un rapport 4/3, sonnant la quarte. Les intervalles consonants qui suivent n'ont été décrits comme tels qu'à la fin du Moyen Âge (notamment par Bartolomé Ramos de Pareja) et à la Renaissance : le rapport 5/4 correspondant à la tierce majeure, le rapport 6/5 à la tierce mineure.

Ces rapports numériques correspondant aux premières consonances, 2/1 (octave), 3/2 (quinte), 4/3 (quarte), 5/4 (tierce majeure) et 6/5 (tierce mineure), les seules qui aujourd'hui encore sont généralement considérées comme consonantes, ont quelques particularités qui ont mené à des conclusions parfois surprenantes :

• ils sont tous « super-particuliers » (ou « épi-mores »), ce qui veut dire que leur numérateur est chaque fois supérieur d'une unité au dénominateur ; on en a parfois conclu un peu vite que les consonances suivantes correspondraient aux rapports super-particuliers suivants, 7/6, 8/7, 9/8, etc., avec un niveau de consonance progressivement décroissant. Mais parce que les rapports 7/6 et 8/7 n'ont pas d'usage direct en musique, on considère généralement que la série des consonances s'arrête à 6/5, la tierce mineure, et que le rapport 9/8 (seconde majeure) et les suivants sont des dissonances. Il faut ajouter à la série des consonances le renversement des premiers intervalles consonants, la sixte mineure (10/4), la sixte majeure (12/5), etc., qui ne sont plus des rapports super-particuliers ;
• ils sont tous « harmoniques », c'est-à-dire formés de nombres entiers, ce qui a mené d'une part à une explication physique du phénomène de consonance, mais d'autre part à quelques utopies concernant la formation des accords. L'idée des rapports harmoniques a entraîné l'idée curieuse que certains accords seraient formés à partir des harmoniques de leur note fondamentale. Mais cette idée se heurte au moins à deux objections. D'abord, elle n'est applicable qu'à certains accords, et encore de manière relativement approximative :
• l'accord parfait majeur se justifierait par les harmoniques 1, 3 et 5, mais l'accord parfait mineur n'est pas justifiable par les harmoniques ;
• l'accord de septième de dominante correspondrait aux harmoniques 1, 3, 5 et 7, mais l'harmonique 7 est trop bas d'un quart de ton et les autres septièmes ne sont pas justifiables de cette manière.

Les accords ne sont pas des combinaisons d'harmoniques, mais bien des superpositions de notes, et chacune de celles-ci s'accompagne de ses propres harmoniques. Les consonances et les accords s'expliquent donc comme des concordances de plusieurs séries harmoniques entre elles. Mais une discussion plus complète de cet aspect appartient à l'article Consonance.

Une première difficulté de la construction des accords a été celle d'imaginer une combinaison de trois sons qui soient entièrement consonante. Il faut considérer les rapports entre trois paires de notes et un instant de réflexion montre qu'il n'existe que quatre possibilités :

1. Superposer une tierce majeure entre les notes 1 et 2 et une tierce mineure entre les notes 2 et 3 ; la distance entre les notes 1 et 3 est d'une quinte − le résultat est l'accord parfait majeur, comme do-mi-sol ;
2. Procéder de même mais en inversant l'ordre des tierces : mineure entre 1 et 2, majeure entre 2 et 3, produisant toujours une quinte entre 1 et 3 – le résultat est l'accord parfait mineur, comme do-mi -sol ;
3. Superposer une tierce majeure et une quarte la distance entre les notes 1 et 3 est une sixte majeure – l'accord qui en résulte s'appelle logiquement accord de sixte majeure, comme do-mi-la ;
4. Procéder de même avec une tierce mineure ; la distance entre les notes 1 et 3 est une sixte mineure – l'accord est celui de sixte mineure, comme
   do-mi -la .

Ces quatre accords sont ceux utilisés au XVI^e siècle, où on commence à les considérer non plus comme des superpositions d'intervalles, mais bien comme des combinaisons formant un tout, des accords au sens propre.

L'étape suivante a été de considérer que les 3^e et 4^e accords (sixte majeure et sixte mineure) étaient des renversements respectivement du 2^e et du 1^er, qu'il pouvaient s'obtenir en transposant à l'octave la première note des accords parfaits : do-mi-sol peut donner mi-sol-do (sixte mineure) et do-mi -sol peut donner mi -sol-do. Le principe du renversement est décrit pour la première fois en 1612, dans la Synopsis musicae novae de Johannes Lippius, qui décrit les accords parfaits majeur et mineur comme la forme « normale », et leur première note comme la « racine » (radix) de l'accord. Le renversement consiste alors à transporter la racine à l'octave supérieure.

À partir de là, on a considéré que la forme normale des accords, leur « forme fondamentale », était celle qui empilait des intervalles de tierce : deux tierce pour les triades (accords parfaits majeur ou mineur, accord de quinte augmentée [formé de deux tierces majeures], de quinte diminuée [formé de deux tierces mineures]), trois tierces pour les accords de septième, etc. Certains auteurs considèrent néanmoins que les accords de sixte (ou de quinte et sixte) peuvent aussi constituer des positions fondamentales : c'est le cas notamment de Hugo Riemann, pour qui l'accord de quinte et sixte est celui que porte normalement le IV^e degré de l'échelle.

Un accord est dit à l'état fondamental lorsque sa basse est la base de l'accord. Cette base est aussi parfois appelée « fondamentale ». Un tel accord n'est pas forcément formé d'un empilement de tierces comme l'accord do-mi-sol. L'ordre des autres notes peut être différent : par exemple, l'accord do-sol-mi est aussi un accord à l'état fondamental. L'accord est dit renversé dans le cas contraire (état non-fondamental). Dans les deux cas, l'accord porte le nom de sa fondamentale (exemple : accord de do majeur). Les autres notes constitutives portent le nom de l'intervalle ascendant qui sépare cette note de la fondamentale, et ceci même si la fondamentale ne se trouve pas à la basse.

Attention : ce nommage est différent du chiffrage de l'accord (basse chiffrée), qui se fait par rapport à la basse et non pas par rapport à la fondamentale – le chiffrage en chiffres romains indique généralement les fondamentales. Il est donc prudent, lorsqu'on parle, par exemple, d'une tierce, de préciser s'il s'agit de la tierce « de l'accord » – autrement dit, la tierce au-dessus de la fondamentale – ou s'il s'agit de la tierce au-dessus de la basse, représentée par le chiffrage, ceci afin d'éviter tout malentendu en cas d'accord renversé.

L'accord est dit à l'état fondamental réduit, ou classé lorsqu'il peut se réduire à une superposition de tierces. Cette réduction s'obtient en abaissant les notes supérieures d'une octave jusqu'à obtenir un empilement de tierces (exemples : do-mi-sol ; do-mi-sol ; do-mi-sol-siré, etc.).

Un accord est constitué d'au moins trois notes distinctes, et pas simplement trois sons musicaux différents : les simultanéités « do, mi, sol » ou « do, fa, la » sont des accords ; par contre, « do, mi, do à l'octave » possède deux notes identiques, c'est un accord incomplet.

Lorsqu'un accord se réduit à une superposition de tierces, il est dit classé (l'harmonie tonale n'étudie que les accords classés). Un accord est ainsi un ensemble d'au moins deux intervalles harmoniques construits depuis un son générateur, produisant une superposition de notes séparées par des tierces (sous sa forme élémentaire).

Les différentes notes appartenant à la superposition de tierces sont appelées notes réelles. La note réelle à partir de laquelle est construite cette superposition est appelée « fondamentale ».

La basse d'un accord est sa note la plus grave. Ce peut être une note réelle ou une note étrangère. Le choix de cette note détermine l'état de l'accord.

À partir de la fondamentale, on nomme les autres notes réelles par le nom de l'intervalle ascendant qui sépare cette note de la fondamentale, et ceci, même si cette fondamentale ne se trouve pas à la basse :

Nom des notes de l'accord

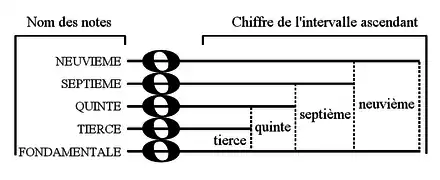
Chaque famille d'accord — ou classe d'accord — est identifiée, soit au moyen du nombre de notes contenues dans l'accord — « accord de trois notes », « accord de quatre notes », etc. —, soit au moyen du nom de la note — « quinte », « septième », etc. — correspondant au plus grand intervalle entre celle-ci et la fondamentale — « accord de quinte », « accord de septième », etc. —, lorsque l'accord est sous la forme d'une superposition de tierces.

L'harmonie tonale étudie essentiellement les trois grandes familles suivantes :

• les accords de trois notes — ou accords de trois sons, ou accords de quinte —, dont les notes réelles — ou notes constitutives — sont la fondamentale, la tierce et la quinte (exemple, « do, mi, sol ») ;
• les accords de quatre notes — ou accords de quatre sons, ou accords de septième —, dont les notes réelles sont celles d'un accord de trois notes, plus une septième (exemple, « do, mi, sol, si♭ »).
• les accords de cinq notes — ou accords de cinq sons, ou accords de neuvième — dont les notes réelles sont celles d'un accord de quatre notes, plus une neuvième (exemple, « do, mi, sol, si♭, ré ») ;

Chaque famille se divise à son tour en plusieurs espèces, compte tenu de la valeur relative des intervalles superposés. Par exemple, selon l'étendue des intervalles considérés, on dénombre quatre espèces d'accord de trois notes, sept espèces d'accord de quatre notes, etc.

Les accords de trois notes dont la quinte est juste — accords dits « parfaits » — sont habituellement considérés comme les seuls accords consonants, les autres formant ce qu'on appelle « l'harmonie dissonante naturelle ».

Lorsqu'un ensemble de sons simultanés ne peut être analysé comme un accord classé — avec ou sans notes étrangères —, il convient de désigner celui-ci sous le vocable d'agrégat. L'étude des agrégats sort du cadre de l'harmonie tonale classique.

L'harmonie tonale ignore les familles d'accords de plus de cinq notes. Les accords dits de onzième tonique et de treizième tonique dont les appellations semblent suggérer des accords de six et sept notes sont respectivement des accords de quatre et cinq notes placés sur la tonique.

En harmonie tonale, certaines notes, dites notes étrangères, peuvent s'ajouter ou se substituer aux notes réelles des accords classés. Celles-ci modifient la couleur de l'accord primitif en ajoutant des dissonances.

Les principaux types de notes étrangères sont : le retard, l'appoggiature, la broderie, la note de passage, l'anticipation, l'échappée, la note altérée, la pédale et la note ajoutée.

L'étude des notes étrangères est habituellement dénommée harmonie dissonante artificielle. Les trois grandes familles d'accords classés, lorsque ceux-ci sont employés sans notes étrangères, forment l'harmonie naturelle.

Un accord au repos est un accord considéré comme une entité isolée, indépendamment de l'accord qui le précède et de celui qui lui succède.

Un accord au repos est caractérisé par son état et par la disposition générale de ses notes. Il peut par ailleurs être chiffré.

L'état d'un accord, qui est déterminé par la note placée à la basse, est sans doute l'aspect le plus important d'un accord au repos. On distingue principalement l'accord fondamental et l'accord renversé.

Mais l'étude de l'harmonie ne se résume pas à un simple travail de classification, de nomenclature et de description des différentes espèces d'accords au repos. Elle consiste également à mettre ceux-ci en mouvement, c'est-à-dire, à les enchaîner les uns aux autres, conformément aux règles mélodiques et harmoniques. Un accord est donc dit en mouvement, ou encore enchaîné, lorsqu'il est considéré par rapport à l'accord précédent et à l'accord suivant.

Tout comme les autres arts, la musique du XX^e siècle connaît un grand nombre de bouleversements et une remise en question des systèmes qui l'ont précédée. C'est ainsi que l'environnement tonal et les accords sont abandonnés par certains musiciens. Cependant, la musique tonale subsiste dans la musique savante, ainsi que dans la musique populaire.