Autorotation

Flux d'air d'autorotation d'un hélicoptère

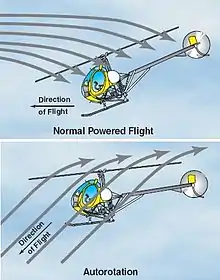
En cas de panne de moteur sur un hélicoptère survenant à une altitude suffisante, la mise en autorotation du rotor principal permet de descendre et d'atterrir sans dommage[2]^,[3]. Lorsque la panne moteur survient, l'embrayage centrifuge permet le désaccouplement du rotor. Il peut ainsi tourner sur son axe. Le pilote intervient sur la commande de pas collectif en l'amenant à sa position minimale. Cette action a pour effet d'inverser l'incidence des pales du rotor principal. De cette façon, l'hélicoptère amorce un mouvement descendant. Relativement au rotor, le flux d'air est donc ascendant. C'est alors lui qui entraîne l'autorotation du rotor dans le même sens, au même titre qu'une éolienne ou un autogire. Il s'agit du mode de fonctionnement en « moulinet ». L'entraînement du rotor par le flux ascendant lui oppose une résistance qui permet la sustentation de l'hélicoptère. Cette résistance aérodynamique équivaut à celle d'un parachute.

D'une manière générale, lorsque la panne moteur survient, l'hélicoptère est en translation horizontale vers l'avant. Pendant la descente en autorotation, l'hélicoptère conserve sa vitesse horizontale. À l'approche du sol, le pilote agit sur le pas cyclique pour cabrer l'appareil ce qui a pour effet de réduire puis d'annuler sa vitesse de translation. Pour atterrir en douceur, le pilote relève enfin la commande de pas collectif afin de réduire puis d'annuler la vitesse de descente au contact du sol[4].

Il convient de noter que l'autorotation concerne principalement les hélicoptères monomoteurs. Pour ces derniers, la validation de l'autorotation est nécessaire à leur certification. Pour les appareils bimoteurs, la fiabilité moteur est telle qu'il est très peu probable que les deux moteurs tombent en panne simultanément.

La vitesse angulaire que prend l’hélice croît lorsque le pas des pales diminue[5].

Équations

Flux d'air à travers le rotor d'un hélicoptère en vol horizontal normal (haut) et en autorotation (bas)

Voici les équations permettant de transformer l'énergie potentielle en énergie cinétique lors d'une mise en autorotation. Suivant les phases de vols, les valeurs de différentes grandeurs vont changer, mais l'équation de conservation d'énergie demeure identique :

${\displaystyle E_{c}+E_{p}+e_{r}=cte}$

avec :

• ${\displaystyle Ec={\frac {1}{2}}\;m\cdot v^{2}}$ l'énergie cinétique de translation de l'hélicoptère
• ${\displaystyle Ep=m\cdot g\cdot z}$ l'énergie potentielle du système Terre et hélicoptère
• ${\displaystyle Er=k\cdot S\cdot v^{3}}$ l'énergie cinétique de rotation du rotor

et :

• m : masse de l'hélicoptère (en kg)
• v : sa vitesse en unité internationale (en m/s, exit les kt)
• g : intensité de pesanteur (souvent 9,81 m/s²)
• z : son altitude (en m, par rapport au sol, celle du point de posée ici)
• k : la constante du coefficient des pales (en kg m⁻³ s)
• S : la section balayée (en m²)

Comment trouver k ? (en fonction de l'hélicoptère ?) Pour k qui est la constante du coefficient des pales dépendant de la vitesse du rotor, on devrait avoir :

• une variable concernant la vitesse de rotation du profil ;
• une variable relative à l'élasticité de la pale ;
• un coefficient de frottement en fonction de la masse volumique de l'air (qui dépendra elle-même de l'altitude)

Pour mémoire : v est la vitesse de rotation du profil à l'instant t considéré, mais en unité SI, ici en m/s (mètre par seconde).

À propos de l'énergie totale de l'hélicoptère

En vol de croisière en ligne droite (vitesse et altitude constante), l'énergie totale de l'hélicoptère est pseudo-constante. Car les forces de frottements (sur les pales et l'hélicoptère) font perdre de l'énergie donc des tours, mais cette perte est exactement compensée par l'énergie apportée par le moteur. Par contre, étant assez haut, si l'hélicoptère est mis en autorotation, le moteur ne fournit plus l'énergie nécessaire à la rotation du ou des rotors, et l'énergie totale de l'hélicoptère va donc diminuer à cause du frottement de l'hélice dans l'air.

L'intégration du frottement dans les équations complique le calcul, mais n'est pas assez négligeable pour ne pas être mentionnée.

L'autorotation présente également un intérêt pour le pilotage des missiles : une autorotation dite « lente » (de l'ordre du tour par seconde) permet de régulariser les effets des éventuelles dissymétries du corps volant (exemple missiles Matra R530, antichars SS.11, air-sol AS-30L, etc.). Une autorotation un peu plus rapide (environ 10 tours par seconde) permet de n'utiliser qu'un seul plan de gouvernes (lacet par exemple) au lieu de deux (lacet-tangage), puisque l'autorotation en roulis distribue son effet tour à tour selon les voies verticales et horizontales (exemples missiles Milan, Roland, Eryx).

Par rapport aux missiles stabilisés en roulis, le pilotage des missiles en autorotation est plus économique, puisqu'il élimine jusqu'à deux des trois chaînes de pilotage (roulis et lacet ou tangage), mais il demande une rapidité de réponse des gouvernes un peu plus élevée (la fréquence de roulis s'ajoute à celle du pilotage), ce qui vaut également pour les équipements embarqués (dans le cas d'un autodirecteur par exemple).

Pour les projectiles tels les roquettes et les obus, l'autorotation encore plus rapide permet un effet de stabilisation par inertie gyroscopique.

• Portail des hélicoptères
• Portail de l’aéronautique