Loi de Lévy

En théorie des probabilités et en statistique, la loi de Lévy, nommée d'après le mathématicien Paul Lévy, est une loi de probabilité continue. En physique, plus précisément en spectroscopie, elle porte le nom de profil de van der Waals et décrit le profil de certaines raies spectrales.

Distribution de Lévy
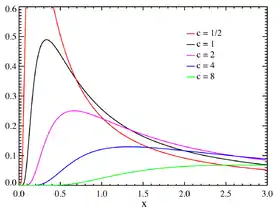Densité de probabilité pour différentes valeurs de c.


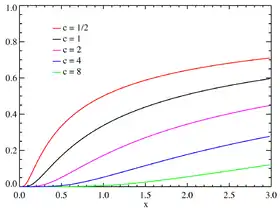Fonction de répartition pour différentes valeurs de c.

Paramètres	$\mu \in \mathbb {R}$ $c>0\,$
Support	$x\in ]\mu ,+\infty [\,$
Densité de probabilité	${\sqrt {\frac {c}{2\pi }}}\cdot {\frac {1}{(x-\mu )^{3/2}}}\mathrm {e} ^{-{\frac {c}{2(x-\mu )}}}$
Fonction de répartition	$\mathrm {erfc} ~{\sqrt {\frac {c}{2(x-\mu )}}}\!$
Espérance	$+\infty \,$
Médiane	$c/2({\textrm {erf}}^{-1}(1/2))^{2}\,$ pour $\mu =0$
Mode	${\frac {c}{3}}\,$ pour $\mu =0$
Variance	$+\infty \,$
Asymétrie	non définie
Kurtosis normalisé	non défini
Entropie	${\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}\,$
Fonction génératrice des moments	non définie
Fonction caractéristique	$e^{i\mu t-{\sqrt {-2ict}}}\,$

Cette loi dépend de deux paramètres : un paramètre de position $\mu \in \mathbb {R}$ qui décale le support $[\mu ,\infty [$ , et un paramètre d'échelle $c$ .

Si X suit une loi de Lévy, on notera : $X\sim \mathrm {Levy} (\mu ,c)$ .

Avec la loi de Cauchy et la loi normale, c'est l'une des trois à être stable par convolution et à posséder une densité de probabilité exprimable analytiquement.

Caractéristiques

Densité de probabilité

La densité de probabilité de la loi de Lévy est donnée par :

f(x;\mu ,c)={\begin{cases}\displaystyle {\sqrt {\frac {c}{2\pi }}}{\frac {1}{(x-\mu )^{3/2}}}e^{-{\frac {c}{2(x-\mu )}}}&{\text{ si }}x>\mu \\0&{\text{ sinon}}\end{cases}}

où $\mu \in \mathbb {R}$ est le paramètre de position et $c>0$ est le paramètre d'échelle. Comme toutes les lois stables, il existe une forme standard de la loi, définie par la densité $f(x;0,1)$ que l'on obtient à partir du changement de variable : $y={\frac {x-\mu }{c}}$ dans l'expression de $f(x;\mu ,\sigma )$ .

La loi de Lévy possède une queue lourde, exprimée par la formule :

f(x;\mu ,c)\,{\underset {x\rightarrow \infty }{\sim }}\,{\sqrt {\frac {c}{2\pi }}}~{\frac {1}{x^{3/2}}}.

Cette propriété est illustrée par la représentation de la densité sur un repère log-log.

Densité de probabilité d la loi de Lévy sur un repère log-log.

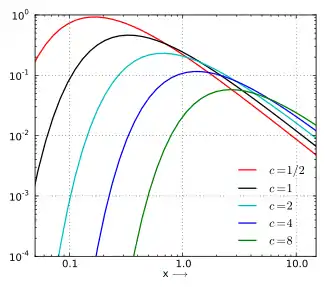
Fonction de répartition

La fonction de répartition de la loi de Lévy est donnée par :

F(x;\mu ,c)={\begin{cases}\displaystyle {\textrm {erfc}}\left({\sqrt {c/2(x-\mu )}}\right)&{\text{ si }}x>\mu \\0&{\text{ sinon}}\end{cases}}

où $erfc$ est la fonction d'erreur complémentaire.

Fonction caractéristique

La fonction caractéristique de la loi de Lévy est :

\varphi (t;\mu ,c)=e^{i\mu t-{\sqrt {-2ict}}}.

On peut écrire cette fonction caractéristique sous la forme plus classique des lois stables :

\varphi (t;\mu ,c)=e^{i\mu t-|ct|^{1/2}~(1-i~{\textrm {sign}}(t))}.

Moments

Pour $\mu =0$ , le n-ième moment de la loi de Lévy est donné formellement par :

m_{n}\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {e^{-c/2x}\,x^{n}}{x^{3/2}}}\,{\rm {d}}x.

Cette intégrale diverge pour tout n>0, ainsi les moments de la loi de Lévy ne sont pas définis. La fonction génératrice des moments est donnée formellement par :

M(t;c)\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {e^{-c/2x+tx}}{x^{3/2}}}\,{\rm {d}}x.

L'intégrale diverge pour $t>0$ et est ainsi non définie sur tout intervalle autour de zéro, la fonction génératrice des moments n'est donc pas définie.

Liens avec d'autres lois

Si $X\sim {\textrm {Levy}}(\mu ,c)\,$ alors $kX+b\sim {\textrm {Levy}}(k\mu +b,kc)\,$
Si $X\,\sim \,{\textrm {Levy}}(0,c)$ alors $X\,\sim \,{\textrm {Inv-Gamma}}({\tfrac {1}{2}},{\tfrac {c}{2}})$ (loi inverse-gamma)
La loi de Lévy est cas particulier de fonction de Pearson de type V.
Si $Y\,\sim \,{\textrm {Normal}}(\mu ,\sigma ^{2})$ (loi normale) alors ${(Y-\mu )}^{-2}\sim \,{\textrm {Levy}}(0,1/\sigma ^{2})$
Si $X\sim {\textrm {Normal}}(\mu ,{\tfrac {1}{\sqrt {\sigma }}})\,$ alors ${(X-\mu )}^{-2}\sim {\textrm {Levy}}(0,\sigma )\,$
Si $X\,\sim \,{\textrm {Levy}}(\mu ,c)$ alors $X\,\sim \,{\textrm {Stable}}(1/2,1,c,\mu )\,$ (loi stable)
Si $X\,\sim \,{\textrm {Levy}}(0,c)$ alors $X\,\sim \,{\textrm {Scale-inv-}}\chi ^{2}(1,c)$ (loi inverse-χ² changée d'échelle)
Si $X\,\sim \,{\textrm {Levy}}(\mu ,c)$ alors ${(X-\mu )}^{-{\tfrac {1}{2}}}\sim \,{\textrm {FoldedNormal}}(0,1/{\sqrt {c}})$ (loi normale repliée)

Référence

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lévy distribution » (voir la liste des auteurs).

Portail des probabilités et de la statistique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.