Loi de mélange
En probabilité et en statistiques, une loi de mélange est la loi de probabilité d'une variable aléatoire s'obtenant à partir d'une famille de variables aléatoires de la manière suivante : une variable aléatoire est choisie au hasard parmi la famille de variables aléatoires donnée, puis la valeur de la variable aléatoire sélectionnée est réalisée. Les variables aléatoires sous-jacentes peuvent être des nombres réels aléatoires, ou des vecteurs aléatoires (chacun ayant la même dimension), auquel cas la répartition du mélange est une répartition à plusieurs variables.
Ne doit pas être confondu avec loi composée.
Dans les cas où chacune des variables aléatoires sous-jacente est continue, la variable finale sera également continue et sa fonction de densité de probabilité est parfois appelée densité de mélange. La fonction de répartition (et la densité de probabilité si elle existe) peut être exprimée sous forme d'une combinaison convexe (par exemple une somme pondérée, avec des probabilités positives dont la somme est 1) d'autres fonctions de loi et de fonctions de densité. Les répartitions individuelles qui sont combinées pour former la loi du mélange sont appelées les composants du mélange, et les probabilités associées à chaque composant sont appelées les probabilités du mélange. Le nombre de composants dans la loi de mélange est souvent limitée, bien que dans certains cas, les composants peuvent être indénombrables.
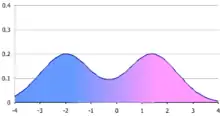
Une distinction doit être faite entre une variable aléatoire dont la loi est une somme pondérée de composants, et une variable qui s'écrit comme la somme de variables aléatoires, auquel cas sa loi est donnée par le produit de convolution des lois des variables sommées. À titre d'exemple, la somme de deux variables aléatoires conjointement normalement distribuées, chacun avec des moyennes différentes, aura toujours une loi normale. D'un autre côté, une densité de mélange conçue comme un mélange de deux lois normales, avec des moyennes différentes, aura deux pics à condition que les deux moyennes soient assez éloignées, ce qui montre que cette loi est radicalement différente d'une loi normale.
La loi de mélange existe dans de nombreux contextes dans la littérature et se pose naturellement là où une population statistique contient deux ou plusieurs sous-populations. Elles sont également parfois utilisées comme moyen de représentation des lois non normales. L'analyse des données concernant les modèles statistiques portant sur les lois de mélange est appelée modèle de mélange.
Mélanges finis et dénombrables
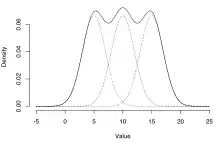
Supposons un ensemble fini de fonctions de densité de probabilité p1(x), …, pn(x), ou des fonctions de loi cumulative correspondant P1(x), …, Pn(x) et des probabilités w1, …, wn tel que wi ≥ 0 et ∑wi = 1, la loi de mélange peut être représenté par écrit, soit la densité, f, ou de la fonction de loi, F, comme une somme (qui, dans les deux cas, est une combinaison convexe):
Ce type de mélange, une somme finie, est appelé un mélange fini. Le cas d'un ensemble infini dénombrable de composants permet .
Mélange indénombrable
Lorsque l'ensemble de lois des composants est indénombrable, le résultat est souvent appelé une loi de probabilité composé. La construction d'une telle loi a une similitude à celle des lois de mélange, soit des additions, soit des intégrales infinies remplaçant les sommations finis utilisés pour les mélanges finis.
Considérons une fonction de densité de probabilité p(x;a) pour une variable x, paramétrée par a. Autrement dit, pour chaque valeur d'une certaine série A, p(x;a) est une fonction de densité de probabilité par rapport à x. Compte tenu d'une fonction de densité de probabilité w (ce qui signifie que w est non négatif et intègre à 1), la fonction
est encore une fonction de densité de probabilité x. Une intégrale similaire peut être écrit pour la fonction de loi cumulative. On notera que les formules ici réduisent le cas d'un mélange fini ou infini si la densité w est autorisé à être une fonction généralisée représentant le «dérivé» de la fonction de loi cumulative d'une loi discrète.
Des mélanges de familles paramétriques
Les constituants de mélange ne sont souvent pas des lois de probabilité arbitraires, mais au contraire sont des membres d'une famille paramétrique, avec valeurs différentes pour un ou des paramètres. Dans ce cas, en supposant qu'il existe, la densité peut être écrit sous la forme d'une somme tel que:
pour un paramètre, ou
pour un paramètre, et ainsi de suite
Propriétés
Convexité
Une combinaison linéaire générale de fonction de densité de probabilité n'est pas nécessairement une densité de probabilité, car il peut être négatif, ou il peut intégrer à autre chose qu'à 1. Toutefois, une combinaison convexe des fonctions de densité de probabilité préserve ces deux propriétés (non-négativité et l'intégration à 1), et donc des densités de mélange sont eux-mêmes des fonctions de densité de probabilité.
Moments
Soit X1, ..., Xn représentent des variables aléatoires à partir de n lois de composants, et soit X représentant une variable aléatoire de la loi de mélange. Ainsi, pour toute fonction H(·) pour lesquels existe, et en supposant que la composante densités pi(x) existe,
Notez que le jième moment de zéro (c'est è dire le choix de H(x) = xj) est simplement une moyenne pondérée du jième moment des composants. Les moments autour de la moyenne H(x) = (x − μ)j implique une expansion binomiale[1]:
où μi désigne la moyenne du iième composant.
Dans le cas d'un mélange de lois unidimensionnelles avec des poids wi, des moyennes μi et des variances σi2, la moyenne et la variance totale sont:
Ces relations mettent en évidence le potentiel des lois de mélange pour afficher les moments non-trivials tels que l'asymétrie et l'aplatissement et multi-modalité[2].
Modes
La question de la multimodalité est simple pour certains cas, tels que des mélanges de lois exponentielles : tous ces mélanges sont uni-modaux[3]. Cependant, pour le cas des mélanges de lois normales, la question est complexe. Les conditions pour le nombre de modes dans un mélange normale multivariée ont été observés par Ray et Lindsay[4] étendant les travaux antérieurs sur l’uni-variété[5],[6] et les lois multivariées (Carreira-Perpinan et Williams, 2003).
Ici, le problème de l'évaluation des modes d'un n mélange de composants dans un espace tridimensionnel D est réduite à l'identification des points critiques (les points minimum, maximum et selle) sur un collecteur appelée la surface crête, qui est l'image de la fonction 'crête'.
où α appartient à la dimension simplexe n − 1 et Σi ∈ RD × D, μi ∈ RD correspondent à la moyenne et la covariance du iième composant. Ray et Lindsay ont considéré le cas où n − 1 < D montrant une correspondance entre les modes de mélange et la fonction d'élévation h(α) = q(x*(α)) ainsi, on peut identifier les modes en résolvant par apport à α et déterminer la valeur x*(α).
En utilisant les outils graphiques, la multi-modalité potentielle de n = {2, 3} mélanges est démontrée; il est en particulier montré que le nombre de modes peut être supérieur à n et que les modes ne peut pas être confondu avec les moyens qui le composent. Pour deux composants, ils développent un outil graphique pour l'analyse de la résolution du précité différentiel par rapport à w1 et exprimer la solution sous forme de fonction Π(α), α ∈ [0, 1] de sorte que le nombre et l'emplacement des modes pour une valeur donnée de w1 correspond au nombre d'intersections du graphe sur la ligne Π(α) = w1. Cela peut être lié au nombre d'oscillations du graphe, et donc à des solutions de explicitse pour un mélange de deux composants homoscédastiques donné par
où dM(μ1, μ2, Σ) = (μ2 − μ1)TΣ−1(μ2 − μ1) est la distance de Mahalanobis.
Comme cette dernière est quadratique, il en resulte un nombre maximal de deux modes, indépendamment de la dimension ou le de la moyenne.
Applications
Les densités de mélange sont des densités compliquées, exprimables en termes de densités plus simples (les composants de mélange), et sont utilisés à la fois car ils fournissent un bon modèle pour certains ensembles de données (où les différents sous-ensembles de données présentent des caractéristiques différentes et peuvent donc être le mieux modélisées). Également parce qu'ils peuvent être plus mathématiquement traitables, qui vient du fait que les composants individuels du mélange peuvent être plus faciles à étudier que la densité globale du mélange.
Les densités de mélange peut être utilisé pour modéliser une population statistique avec des sous-populations, où les composants du mélange sont les densités des sous-populations, et les moyennes sont les proportions de chaque sous-population dans la population globale.
Les densités de mélange peut également être utilisé pour modéliser l'erreur expérimentale.
Les statistiques paramétriques qui ne supposent aucune erreur échouent souvent sur de telles densités de mélange, par exemple, les statistiques qui supposent la normalité échouent souvent désastreusement en présence même de quelques valeurs aberrantes. Pour éviter ce problème, on utilise des statistiques robustes.
Dans une méta-analyse des études différentes, l'hétérogénéité des études provoque la loi des résultats à une loi de mélange, et conduit à surdispersion des résultats relatifs à l'erreur prédite. Par exemple, dans un sondage, la marge d'erreur (déterminé par la taille de l'échantillon) prédit l'erreur d'échantillonnage, et donc la dispersion des résultats sur des enquêtes répétées. La présence de l'hétérogénéité de l'étude (les études ont différents biais d'échantillonnage) augmente la dispersion par rapport à la marge d'erreur.
En apprentissage automatique, l'algorithme de partitionnement non supervisé des K-moyennes peut-être vu optimisant la vraisemblance d'un k-mélange gaussien avec les données observées. Des variations de l'algorithme des K-moyennes sont possibles en adoptant ce point de vue.
Voir aussi
Modèles hiérarchiques
Références
- Frühwirth-Schnatter (2006, Ch.1.2.4)
- J. S. Marron et M. P. Wand, « Exact Mean Integrated Squared Error », The Annals of Statistics, vol. 20, no 2, , p. 712-736
- Frühwirth-Schnatter (2006, Ch.1)
- Ray, R.; Lindsay, B. (2005), "The topography of multivariate normal mixtures", The Annals of Statistics 33 (5): 2042–2065
- Robertson CA, Fryer JG (1969) Some descriptive properties of normal mixtures.
- Behboodian J (1970) On the modes of a mixture of two normal distributions.
Lecture supplémentaire
- Frühwirth-Schnatter, Sylvia (2006), Finite Mixture and Markov Switching Models, Springer, (ISBN 978-1-4419-2194-9)
- Lindsay, Bruce G. (1995), Mixture models: theory, geometry and applications, NSF-CBMS Regional Conference Series in Probability and Statistics 5, Hayward, CA, USA: Institute of Mathematical Statistics, (ISBN 0-940600-32-3)
- Portail des mathématiques
- Portail des probabilités et de la statistique