Dualité onde-corpuscule

En physique, la dualité onde-corpuscule est un principe selon lequel tous les objets physiques peuvent présenter parfois des propriétés d'ondes et parfois des propriétés de corpuscules. La manifestation de ces propriétés ne dépend pas seulement de l'objet étudié isolément, mais aussi de tout l'appareillage de mesure utilisé. Ce concept fait partie des fondements de la mécanique quantique. Le cas d'école est celui de la lumière, qui présente deux aspects complémentaires selon les conditions d'expérience : elle apparait soit ondulatoire, d’où le concept de longueur d’onde, soit corpusculaire, d'où le concept de photons.

Les impacts des particules rendent visible l'interférence des ondes, comme dans l'expérience des fentes de Young, par exemple.
Un paquet d'ondes qui représente une particule quantique
Interférence d'une particule quantique avec elle-même

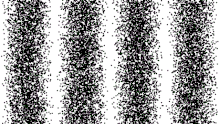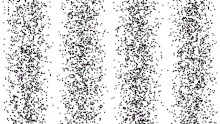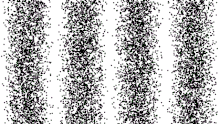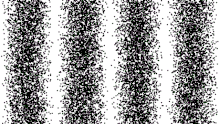
Cette dualité démontre en réalité l'inadéquation - ou plus exactement l'incomplétude - de chacune des conceptions classiques de « corpuscules » ou d'« ondes » pour décrire le comportement des objets quantiques. L'idée de la dualité prend ses racines dans un débat remontant aussi loin que le XVIIe siècle, quand s'affrontaient les théories concurrentes de Christian Huygens, qui considérait que la lumière était composée d'ondes, et celle de Isaac Newton, qui considérait la lumière comme un flot de corpuscules. La dualité onde-corpuscule est introduite en par Albert Einstein pour la lumière[1],[2],[3],[4]. À la suite des travaux d'Einstein, de Louis de Broglie et de bien d'autres, les théories scientifiques modernes accordent à tous les objets une double nature d'onde et de corpuscule, bien que ce phénomène ne soit perceptible qu'à l'échelle des systèmes quantiques.

L'électrodynamique quantique donne à la lumière un aspect corpusculaire, et montre par des propriétés probabilistes que les photons peuvent avoir un comportement ondulatoire.

Approches vulgarisées

La dualité onde-corpuscule vient du fait que les analogies classiques de l'onde (associée à une vague sur l'eau) et du corpuscule (associé à une bille) sont incompatibles : intuitivement et ontologiquement, elles ne peuvent caractériser un même objet.

Le phénomène d'une onde sur l'eau peut certes être considéré compatible avec le caractère corpusculaire des molécules composant l'eau; néanmoins il s'agit là d'un phénomène d'échelle, le caractère ondulatoire observé sur l'eau découlant de la quantité de molécules d'eau composant le milieu, et non de chaque molécule.

Or au début de la physique quantique, les expériences montraient pourtant que les phénomènes observés présentaient bel et bien intrinsèquement ces deux propriétés apparemment opposées.

Propriétés macroscopiques des ondes et corpuscules
CorpusculeOnde
Position ou interaction localisée, d'extension définie délocalisée, d'extension infinie dans le temps et l'espace
Propagation trajectoire continue, avec une vitesse définie et observable diffusion en même temps dans toutes les directions (son "moment" virtuel n'est pas directement observable)
Dénombrabilité et séparabilité l'objet est dénombrable, et séparable en objets distincts. l'objet est indénombrable et inséparable en objets distincts.

La métaphore du cylindre
Métaphore du cylindre : objet ayant à la fois les propriétés d'un disque et d'un rectangle

La métaphore du cylindre est l'exemple d'un objet ayant des propriétés apparemment inconciliables. Il serait à première vue déroutant d'affirmer qu'un objet ait à la fois les propriétés d'un disque et d'un rectangle : sur un plan, un objet est soit un disque, soit un rectangle.

Mais si l'on considère un cylindre : une projection suivant l'axe du cylindre donne un disque, et une projection perpendiculairement à cet axe donne un rectangle.

De la même manière, « onde » et « corpuscule » sont des manières de voir les choses et non les choses en elles-mêmes. Le terme de dualité est alors assez "contradictoire", signifiant qu'il existe deux choses différentes alors qu'il s'agit bien de l'unification de deux domaines de la physique : les ondes et l'aspect corpusculaire.

Notons par ailleurs que dans la description mathématique de la physique quantique, le résultat de la mesure est similaire à une projection géométrique (notion d'observable : l'état de l'objet est décrit par des nombres que l'on peut voir comme des coordonnées dans une base vectorielle, et en géométrie euclidienne, les coordonnées sont la projection de l'objet sur les axes de référence).

C’est l’absence d’équivalent macroscopique sur quoi nous pourrions nous référer qui nous force à penser les objets quantiques comme possédant des attributs contradictoires. Il serait inexact de dire que la lumière (comme tout autre système quantique d’ailleurs) est à la fois une onde et un corpuscule, elle n’est ni l’un, ni l’autre. Le manque d'un vocabulaire adéquat et l'impossibilité de se faire une représentation mentale intuitive des phénomènes à petite échelle nous font voir ces objets comme ayant une nature, par elle-même, antinomique.

Pour lever cet apparent paradoxe et insister sur l'imperfection de nos concepts classiques d'onde et de corpuscule, les physiciens Jean-Marc Lévy-Leblond et Françoise Balibar ont proposé d'utiliser le terme de « quanton » pour parler d'un objet quantique. Un quanton n'est ni une onde, ni un corpuscule, mais peut présenter les deux aspects selon le principe de complémentarité de Bohr.

La gnoséologie cartésienne utilise cette idée pour démontrer que nos sens nous trompent. Descartes prend cet exemple : « Comme aussi une tour carrée, étant vue de loin, paraît ronde[5]. » Descartes utilise la même métaphore : des objets ou des formes géométriques différents ayant les propriétés de l'un et de l'autre (mais ils ne sont ni l'un, ni l'autre).

Histoire

La dualité onde-corpuscule s'est imposée au terme d'une longue histoire où les aspects purement ondulatoires et corpusculaires ont été tour à tour privilégiés. Ces aspects ont tout d'abord été mis en évidence avec les théories de la lumière, avant d'être étendus — au XXe siècle — à tous les objets physiques.

Huygens et Newton

La première théorie complète de la lumière a été établie par le physicien néerlandais Christian Huygens au XVIIe siècle. Il proposait une théorie ondulatoire de la lumière et a en particulier démontré que les ondes lumineuses pouvaient interférer de manière à former un front d'onde se propageant en ligne droite. Toutefois, sa théorie possédait certaines limitations en d'autres domaines et fut bientôt éclipsée par la théorie corpusculaire de la lumière établie à la même époque par Isaac Newton.

Newton proposait une lumière constituée de corpuscules, expliquant ainsi simplement les phénomènes de réflexion optique. Au prix de complications considérables, cette théorie pouvait également expliquer les phénomènes de réfraction à travers une lentille, et de dispersion d'un faisceau lumineux à travers un prisme.

Bénéficiant de l'immense prestige de Newton, cette théorie ne fut guère remise en question pendant plus d'un siècle.

Fresnel, Maxwell et Young

Au début du XIXe siècle, les expériences de diffraction faites par Thomas Young (fentes de Young) et Augustin Fresnel (miroirs de Fresnel) ont démontré la pertinence des théories de Christian Huygens : ces expériences prouvèrent que quand la lumière est envoyée sur un réseau de diffraction, on observe un motif d'interférence caractéristique, très semblable aux motifs résultant de l'interférence d'ondulations sur l'eau; la longueur d'onde de la lumière peut être calculée à partir de tels motifs.

Le point de vue ondulatoire n'a pas remplacé immédiatement le point de vue corpusculaire, mais s'est imposé peu à peu à la communauté scientifique au cours du XIXe siècle, surtout grâce à l'explication en 1821 par Augustin Fresnel du phénomène de polarisation de la lumière que ne pouvait expliquer l'autre approche, puis à la suite de l'expérience menée en 1850 par Léon Foucault sur la vitesse de propagation de la lumière. Ces équations furent vérifiées par maintes expériences et le point de vue de Huygens devint largement admis.

James Maxwell, dans la seconde moitié du XIXe siècle, expliqua la lumière en tant que propagation d'ondes de perturbations électromagnétiques avec ses équations de Maxwell.

Einstein et les photons

En 1905, Albert Einstein réintroduisit l'idée que la lumière pouvait avoir une nature corpusculaire : il expliqua l'effet de seuil de l'effet photoélectrique en postulant l'existence de quanta d'énergie lumineuse. Einstein admit que la fréquence ν (nu) de cette lumière est liée à l'énergie E des photons par la relation de Planck :

où h est la constante de Planck (6,626 × 10-34J s).

Cette relation prit le nom de relation de Planck-Einstein[6].

Cette vision fut contestée très longtemps[7], en particulier parce qu'elle ne s'accorde pas facilement avec les comportements spécifiquement ondulatoires tels que la diffraction.

De Broglie

En 1924, dans sa thèse[8], Louis de Broglie affirma que toute matière (et pas seulement la lumière) a une nature ondulatoire. Il associa la quantité de mouvement p d'une particule à une longueur d'onde λ, appelée longueur d'onde de de Broglie :

C'est une généralisation de la relation de Planck-Einstein indiquée ci-dessus, car la quantité de mouvement (ou l'impulsion) d'un photon est donnée par où c est la vitesse de la lumière dans le vide, et (si on remplace p et dans l'équation de de Broglie, on retrouve la relation de Planck-Einstein).

La formule exprimée par De Broglie fut confirmée trois ans après par Clinton J. Davisson et Lester H. Germer. Ceux-ci dirigèrent un faisceau d'électrons, qui contrairement aux photons ont une masse, vers un réseau de diffraction cristallin : les motifs d'interférence attendus purent ainsi être observés.

Exemple de molécule de fullerène

Des expériences semblables ont été entreprises depuis avec des protons et même avec des molécules entières, avec notamment l'expérience d'Estermann et Otto Stern en 1929, et la formule a été confirmée dans tous les cas.

De Broglie reçut en 1929 le prix Nobel de physique pour son hypothèse, qui influença profondément la physique de cette époque.

En 1999, des chercheurs de l'Université de Vienne ont fait diffracter du fullerène (molécule C60). Dans cette expérience, la longueur d'onde de de Broglie était de 2,5 pm alors que la molécule a un diamètre d'environ 1 nm, soit 400 fois supérieur. C'était alors l'objet physique le plus complexe qui montrait un comportement ondulatoire[9].

Électrodynamique quantique

Avec un photomultiplicateur il est possible de détecter un photon isolé, et un photon de même couleur produit toujours dans cet appareil un événement de même intensité[10]. Plus généralement, tous les appareils que l'on a fabriqués pour la détection de faibles intensités lumineuses amènent à la même conclusion : la lumière est faite de particules, alors que toutes ses manifestations dans la vie quotidienne semblent dues à des phénomènes ondulatoires[11].

L'expérience qui intriguait déjà Isaac Newton est celle de la réflexion de la lumière sur la surface d'un objet en verre : il y a toujours 4 % des rayons ou des photons qui sont réfléchis (les autres 96 % le traversent)[12]. Si au lieu d'une surface on compte les réflexions sur une plaque de verre composée de deux surfaces parfaitement parallèles, on s'attend à un résultat de 8 % (le double du résultat obtenu avec une surface simple) ; mais, l'expérience montre un phénomène qui ressemble à une interférence : en augmentant progressivement l'épaisseur de la plaque, la réflexion de la lumière varie de manière cyclique entre 0 et 16 %[13]. Ce phénomène a pu être expliqué par une théorie ondulatoire qui prédisait que l'intensité détectée baisserait avec celle de la lumière émise, ce qui a tenu jusqu'au moment où les photomultiplicateurs ont été capables de détecter des photons uniques : l'intensité détectée ne baissait pas avec la diminution de la lumière émise. Les physiciens ont alors accepté la dualité onde-corpuscule comme un fait[14].

L'électrodynamique quantique a résolu ce paradoxe, sans pour autant l'expliquer, en considérant que le verre (ou toute autre matière translucide) réfléchit les photons selon une probabilité donnée. À partir de ce postulat, la théorie est capable d'expliquer tous les phénomènes lumineux que l'on croyait ondulatoires[15].

Mise en évidence de la dualité
Figure 1 : Schéma de l'expérience.

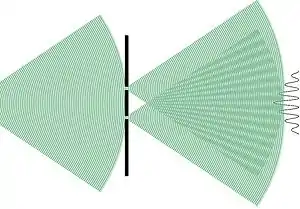
Une des manières les plus claires de mettre en évidence la dualité onde-corpuscule est l'expérience des fentes de Young. Cette expérience est connue depuis le XIXe siècle, où elle a d'abord mis clairement en évidence l'aspect ondulatoire de la lumière. Modifiée de manière adéquate, elle peut démontrer de manière spectaculaire la dualité onde-corpuscule, non seulement de la lumière mais aussi de tout autre objet quantique. Dans la description qui suit, il sera question de lumière et de photons mais il ne faut pas perdre de vue qu'elle est également applicable - du moins en principe - à tout autre corpuscule (par exemple des électrons), et même à des atomes et à des molécules.

Figure 2 : figure d'interférence observée.

L'expérience consiste à éclairer par une source lumineuse un écran percé de deux fentes très fines et très rapprochées. Ces deux fentes se comportent comme deux sources secondaires d'émission lumineuse. Une plaque photographique placée derrière l'écran enregistre la lumière issue des deux fentes (⇐ voir figure 1).

Ces deux sources interfèrent et forment sur la plaque photographique ce que l'on appelle une figure d'interférence (voir figure 2 ⇒). Cette figure est caractéristique d'un comportement ondulatoire de la lumière (voir l'article interférence). Si l'expérience en reste à ce niveau, l'aspect corpusculaire n'apparaît pas.

Figure 4 : figure d'interférence constituée petit à petit

En fait, il est possible de diminuer l'intensité lumineuse de la source primaire de manière que la lumière soit émise photon par photon. Le comportement de la lumière devient alors inexplicable sans faire appel à la dualité onde-corpuscule.

Figure 3 : expérience avec de « vraies » particules, par exemple des micro-billes.

En effet, si on remplace la source lumineuse par un canon qui tire des micro-billes à travers les deux fentes (par exemple), donc de "vrais" corpuscules, on n'obtient aucune figure d'interférence, mais simplement une zone plus dense, en face des fentes (⇐ voir figure 3).

Or, dans le cas des photons, on retrouve la figure d'interférence reconstituée petit à petit, à mesure que les photons apparaissent sur la plaque photographique (figure 4 ⇒). On retrouve donc une figure d'interférence, caractéristique des ondes, en même temps qu'un aspect corpusculaire des impacts sur la plaque photographique.

L'interprétation de cette expérience est difficile, car si on considère la lumière comme une onde, alors les points d'impacts sur la plaque photographique sont inexplicables; on devrait voir dans ce cas très faiblement, dès les premiers instants, la figure d'interférence de la figure 2, puis de plus en plus intense. Au contraire, si on considère la lumière comme étant exclusivement composée de corpuscules, alors les impacts sur la plaque photographique s'expliquent aisément, mais la figure d'interférence ne s'explique pas : comment et pourquoi certaines zones seraient privilégiées et d'autres interdites à ces corpuscules ?

Force est donc de constater la dualité onde-corpuscule des photons (ou de tout autre objet quantique), qui présentent simultanément les deux aspects.

Interprétation de la dualité
Interférence des ondes de probabilité

En mécanique quantique, la dualité onde-corpuscule est expliquée comme ceci : tout système quantique et donc toute particule est décrit par une fonction d'onde qui représente la densité de probabilité[n 1] de toute variable mesurable (nommée aussi observable). La position d'une particule est un exemple d'une de ces variables. Donc, avant qu'une observation soit faite, la position de la particule est décrite en termes d'ondes de probabilité.

Les deux fentes peuvent être considérées comme deux sources secondaires pour ces ondes de probabilité : les deux ondes se propagent à partir de celles-ci et interfèrent (voir schéma de droite ⇒).

Sur la plaque photographique, il se produit ce que l'on appelle une réduction du paquet d'onde, ou une décohérence de la fonction d'onde : le photon se matérialise, avec une probabilité donnée par la fonction d'onde : élevée à certains endroits (frange brillante), faible ou nulle à d'autres (franges sombres).

La particule se matérialise très clairement aux points rouges de la plaque cible, et pas du tout aux points noirs, là où les ondes créent une interférence destructive.

Cette expérience illustre également une caractéristique essentielle de la mécanique quantique : avant qu'une observation (ou mesure) soit faite, la position d'une particule est décrite en termes d'ondes de probabilité, mais après l'observation (ou mesure) de la particule, elle est décrite par une valeur précise. Ce phénomène se comprend par les inégalités d'Heisenberg, mais s'interprète comme le fait que soit l'on décrit l'objet d'un point de vue particulaire soit d'un point de vue ondulatoire. Il faut faire un choix que la méthode expérimentale va déterminer, par la mesure[16].

La manière de conceptualiser le processus de la mesure est l'une des grandes questions ouvertes de la mécanique quantique. L'interprétation standard est l'interprétation de Copenhague, mais la théorie de la décohérence est aussi de plus en plus considérée par la communauté scientifique. Voir l'article Problème de la mesure quantique pour une discussion approfondie.

Notes et références

Note
  1. C'est-à-dire la probabilité que la variable prenne une valeur donnée à un endroit et à un instant donné.

Références
  1. Cohen-Tannoudji, Dupont-Roc et Grynberg 2001, III, compl. AIII, introd., p. 206.
  2. Paty 1988, p. 102.
  3. Roux 2011, introd., p. 27.
  4. Texier 2015, chap. 1er, § 1.5, p. 25.
  5. René Descartes, La Dioptrique, (lire sur Wikisource), « Discours 6e : De la vision »
  6. Daniel Fredon, Salvério Calléa et Didier Magloire, Toute la MPSI en fiches : Maths.Physique.Chimie, Dunod, coll. « J'intègre », 2013, 512 p. (ISBN 978-2-10-060059-5), p. 219.
  7. (fr) Thèse de Louis de Broglie p. 28-29
  8. (fr) Thèse de Louis de Broglie
  9. (en) M. Arndt, O. Nairz, J. Voss-Andreae, C. Keller, G. van der Zouw et A. Zeilinger, « Wave-particle duality of C60 », Nature, vol. 401,‎ , p. 680-682.
  10. Feynman 1992, p. 30.
  11. Feynman 1992, p. 32.
  12. Feynman 1992, p. 34.
  13. Feynman 1992, p. 38-39.
  14. Feynman 1992, p. 41.
  15. Feynman 1992, p. 42.
  16. Dominique Lefebvre, « Dualité onde - corpuscule », sur www.tangentex.com (consulté le )

Voir aussi

Bibliographie

Articles connexes

Liens externes
  • Portail de la physique
  • Portail de l’optique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.