Effet Zénon quantique

L'effet quantique Zénon (également connu sous le nom de paradoxe de Turing) est une caractéristique des systèmes de mécanique quantique, permettant d'arrêter l'évolution temporelle d'une particule en la mesurant assez fréquemment par rapport à un paramètre de mesure choisi[1].

Avec le nombre croissant de mesures, la fonction d'onde a tendance à rester dans sa forme initiale. Dans l'animation, une évolution libre dans le temps d'une fonction d'onde, représentée à gauche. Dans la partie centrale, elle est interrompue par des mesures de position occasionnelles qui localisent la fonction d'onde dans l'un des neuf secteurs. À droite, une série de mesures très fréquentes conduit à l'effet Zénon.

Parfois, cet effet est interprété comme « un système ne peut pas changer pendant que vous le regardez »[2]. On peut « figer » l'évolution du système en le mesurant assez fréquemment dans son état initial connu. Le sens du terme s'est depuis élargi, conduisant à une définition plus technique, dans laquelle l'évolution du temps peut être supprimée non seulement par la mesure : l'effet quantique Zénon est la suppression de l'évolution unitaire du temps dans les systèmes quantiques fournie par une variété de sources : mesure, interactions avec l'environnement, champs stochastiques, entre autres[3]. À la suite de l'étude de l'effet quantique Zénon, il est devenu évident que l'application d'une série d'impulsions suffisamment fortes et rapides avec une symétrie appropriée peut également découpler un système de son environnement de décohésion[4].

Le nom vient du paradoxe de la flèche de Zénon, qui stipule que parce qu'une flèche en vol ne bouge pas pendant un seul instant, elle ne peut pas bouger du tout. La première dérivation rigoureuse et générale de l'effet quantique Zénon a été présentée en 1974 par Degasperis, Fonda et Ghirardi[5], bien qu'elle ait été précédemment décrite par Alan Turing[6]. La comparaison avec le paradoxe de Zénon est due à un article de 1977 de George Sudarshan et Baidyanath Misra[7].

Selon le postulat de réduction, chaque mesure provoque l'effondrement de la fonction d'onde à un état propre de la base de mesure. Dans le contexte de cet effet, une observation peut simplement être l'absorption d'une particule, sans avoir besoin d'un observateur au sens conventionnel du terme. Cependant, il existe une controverse sur l'interprétation de l'effet, parfois appelé « ⁣ problème de mesure » en traversant l'interface entre les objets microscopiques et macroscopiques[8],[9].

Un autre problème crucial lié à l'effet est strictement lié à la relation d'indétermination temps-énergie (partie du principe d'incertitude). Si l'on veut rendre le processus de mesure de plus en plus fréquent, il faut diminuer en conséquence la durée de la mesure elle-même. Mais la demande que la mesure ne dure que très peu de temps implique que la propagation énergétique de l'état dans lequel se produit la réduction devient de plus en plus grande. Cependant, les écarts par rapport à la loi de décroissance exponentielle pour de petits temps sont liés de manière cruciale à l'inverse de la propagation de l'énergie, de sorte que la région dans laquelle les écarts sont appréciables se rétrécit lorsque l'on raccourcit de plus en plus la durée du processus de mesure. Une évaluation explicite de ces deux demandes concurrentes montre qu'il est inapproprié, sans tenir compte de ce fait fondamental, de traiter de la survenance et de l'émergence effectives de l'effet Zénon[10].

Étroitement lié (et parfois non distingué de l'effet quantique Zénon) est l'effet de chien de garde, dans lequel l'évolution temporelle d'un système est affectée par son couplage continu à l'environnement[11],[12],[13],[14].

Description

Les systèmes quantiques instables devraient présenter un écart de courte durée par rapport à la loi de décroissance exponentielle[15],[16]. Ce phénomène universel a conduit à la prédiction que des mesures fréquentes au cours de cette période non exponentielle pourraient inhiber la désintégration du système, une forme de l'effet quantique Zénon. Par la suite, il a été prédit que des mesures appliquées plus lentement pourraient également améliorer les taux de désintégration, un phénomène connu sous le nom d'effet anti-Zénon quantique[17].

En mécanique quantique, l'interaction évoquée est appelée « mesure » car son résultat peut être interprété en termes de mécanique classique. Une mesure fréquente interdit la transition. Il peut s'agir d'une transition d'une particule d'un demi-espace à un autre (qui pourrait être utilisé pour un miroir atomique dans un nanoscope atomique[18]) comme dans le problème du temps d'arrivée[19],[20], une transition d'un photon dans un guide d'ondes d'un mode à un autre, et il peut s'agir d'une transition d'un atome d'un état quantique à un autre. Il peut s'agir d'une transition du sous-espace sans perte de décohérance d'un qubit à un état avec un qubit perdu dans un ordinateur quantique[21],[22]. En ce sens, pour la correction du qubit, il suffit de déterminer si la décohérence a déjà eu lieu ou non. Tous ces éléments peuvent être considérés comme des applications de l'effet Zénon[23]. De par sa nature, l'effet n'apparaît que dans les systèmes avec des états quantiques distinguables, et est donc inapplicable aux phénomènes classiques et aux corps macroscopiques.

Le mathématicien Robin Gandy a rappelé la formulation de Turing de l'effet quantique Zénon dans une lettre à son collègue mathématicien Max Newman, peu de temps après la mort de Turing :

« Il est facile de montrer, à l'aide de la théorie standard, que si un système commence dans un état propre d'une certaine observable et que des mesures sont effectuées sur cette observable N fois par seconde, alors, même si l'état n'est pas stationnaire, la probabilité que le système soit dans le même état après, disons, une seconde, tend vers un lorsque N tend vers l'infini ; autrement dit, les observations continues empêcheront le mouvement. Alan et moi avons confronté un ou deux physiciens théoriques à cette question, et ils l'ont plutôt balayée d'un revers de main en disant que l'observation continue n'était pas possible. Mais il n'y a rien dans les livres standards (par exemple, celui de Dirac) à cet effet, de sorte qu'au moins le paradoxe montre une insuffisance de la théorie quantique telle qu'elle est habituellement présentée. »

— Cité par Andrew Hodges dans Mathematical Logic, R. O. Gandy and C. E. M. Yates, eds. (Elsevier, 2001), p. 267.

À la suite de la suggestion de Turing, l'effet quantique Zénon est aussi parfois connu sous le nom de paradoxe de Turing. L'idée est implicite dans les premiers travaux de John von Neumann sur les fondements mathématiques de la mécanique quantique, et en particulier la règle parfois appelée postulat de réduction[24]. Il a été montré plus tard que l'effet quantique Zénon d'un système unique équivaut à l'indétermination de l'état quantique d'un système unique[25],[26],[27].

Diverses réalisations et définition générale

Le traitement de l'effet Zénon comme un paradoxe ne se limite pas aux processus de désintégration quantique. En général, le terme effet Zénon est appliqué à diverses transitions, et parfois ces transitions peuvent être très différentes d'une simple "décroissance" (qu'elle soit exponentielle ou non exponentielle).

Une réalisation fait référence à l'observation d'un objet (flèche de Zénon ou toute particule quantique) alors qu'il quitte une région de l'espace. Au 20ᵉ siècle, le piégeage (confinement) d'une particule dans une région par son observation à l'extérieur de la région était considéré comme un non-sens, indiquant une incomplétude de la mécanique quantique[28]. Encore en 2001, le confinement par absorption était considéré comme un paradoxe[29]. Plus tard, des effets similaires de la suppression de la diffusion Raman ont été considérés comme un effet attendu[30],[31],[32], et non pas comme un paradoxe. L'absorption d'un photon à une certaine longueur d'onde, la libération d'un photon (par exemple celui qui s'est échappé d'un certain mode d'une fibre), ou même la relaxation d'une particule lorsqu'elle pénètre dans une région, sont tous des processus qui peuvent être interprétés comme la mesure. Une telle mesure supprime la transition, et est appelée l'effet Zénon dans la littérature scientifique.

Afin de couvrir tous ces phénomènes (y compris l'effet original de suppression de la désintégration quantique), l'effet Zénon peut être défini comme une classe de phénomènes dans lesquels une transition est supprimée par une interaction - une qui permet l'interprétation de l'état résultant dans les termes « la transition ne s'est pas encore produite » et « la transition s'est déjà produite », ou « la proposition que l'évolution d'un système quantique est arrêtée » si l'état du système est mesuré en continu par un appareil macroscopique pour vérifier si le système est encore dans son état initial[33].

Mesure périodique d'un système quantique

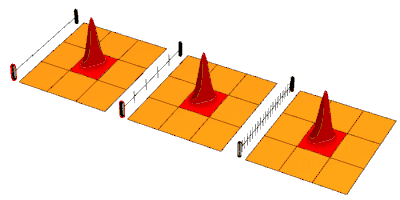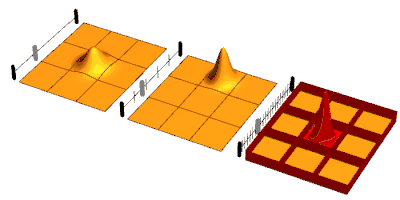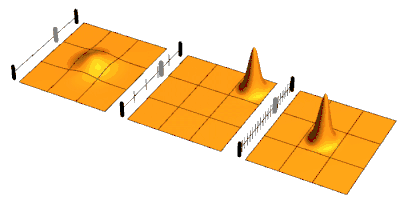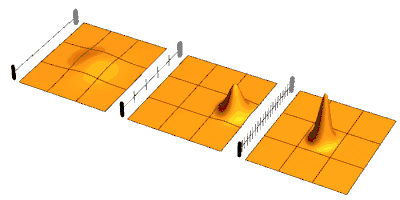
Considérons un système dans un état , qui est l'état propre d'un opérateur de mesure. Supposons que le système sous évolution en temps libre se désintègre avec une certaine probabilité dans l'état . Si des mesures sont effectuées périodiquement, avec un intervalle fini entre chacune, à chaque mesure, la fonction d'onde s'effondre à un état propre de l'opérateur de mesure. Entre les mesures, le système évolue de cet état propre vers un état de superposition des états et . Lorsque l'état de superposition est mesuré, il s'effondrera à nouveau, soit de nouveau dans l'état comme dans la première mesure, ou loin dans l'état . Cependant, sa probabilité de s'effondrer dans l'état après un très court laps de temps est proportionnel à , puisque les probabilités sont proportionnelles aux amplitudes au carré et que les amplitudes se comportent de manière linéaire. Ainsi, dans la limite d'un grand nombre d'intervalles courts, avec une mesure à la fin de chaque intervalle, la probabilité de passer à passe à zéro.

Selon la théorie de la décohérence, l'effondrement de la fonction d'onde n'est pas un événement discret et instantané. Une « mesure » équivaut à coupler fortement le système quantique à l'environnement thermique bruité pendant une brève période de temps, et un couplage fort et continu équivaut à une « mesure » fréquente. Le temps qu'il faut pour que la fonction d'onde « s'effondre » est lié au temps de décohérence du système lorsqu'il est couplé à l'environnement. Plus le couplage est fort, et plus le temps de décohérence est court, plus il s'effondrera rapidement. Ainsi, dans l'image de décohérence, une mise en œuvre parfaite de l'effet quantique Zénon correspond à la limite où un système quantique est continuellement couplé à l'environnement, et où ce couplage est infiniment fort, et où « l'environnement » est une source infiniment grande d'énergie thermique aléatoire.

Expériences et discussions

Expérimentalement, une forte suppression de l'évolution d'un système quantique due au couplage environnemental a été observée dans un certain nombre de systèmes microscopiques.

En 1989, David J. Wineland et son groupe du NIST [34] observé l'effet quantique Zénon pour un système atomique à deux niveaux qui a été interrogé au cours de son évolution. Environ 5 000 ions 9Be+ ont été stockés dans un piège de Penning cylindrique et refroidis au laser à moins de 250 mK. Une impulsion radio-fréquence résonante a été appliquée, qui, si elle était appliquée seule, ferait migrer toute la population de l'état fondamental dans un état excité. Après l'application de l'impulsion, les ions ont été surveillés pour les photons émis en raison de la relaxation. Le piège à ions a ensuite été régulièrement "mesuré" en appliquant une séquence d'impulsions ultraviolettes pendant l'impulsion radio-fréquence. Comme prévu, les impulsions ultraviolettes ont supprimé l'évolution du système vers l'état excité. Les résultats étaient en bon accord avec les modèles théoriques. Une revue récente décrit les travaux ultérieurs dans ce domaine[35].

En 2001, Mark G. Raizen et son groupe de l'Université du Texas à Austin ont observé l'effet quantique Zénon pour un système quantique instable[36], comme proposé à l'origine par Sudarshan et Misra[37]. Ils ont également observé un effet anti-Zénon. Des atomes de sodium ultrafroids ont été piégés dans un réseau optique d'accélération et la perte due à l'effet tunnel a été mesurée. L'évolution a été interrompue en réduisant l'accélération, arrêtant ainsi l'effet tunnel quantique. Le groupe a observé une suppression ou une augmentation du taux de décroissance, selon le régime de mesure.

En 2015, Mukund Vengalattore et son groupe de l'Université Cornell ont démontré un effet Zénon quantique comme étant la modulation du taux d'effet tunnel quantique dans un réseau de gaz ultrafroid, variant selon l'intensité de la lumière utilisée pour imager les atomes[38].

L'effet quantique Zénon est utilisé dans les magnétomètres atomiques commerciaux et naturellement par le mécanisme sensoriel de la boussole magnétique des oiseaux (magnétoréception)[39].

La question reste ouverte jusqu'à quel point on peut approcher la limite d'un nombre infini d'interrogations en raison de l'incertitude d'Heisenberg impliquée dans des temps de mesure plus courts. Il a été montré, cependant, que des mesures effectuées à une fréquence finie peuvent produire des effets Zénon arbitrairement forts[40]. En 2006, Streed et al. au MIT a observé la dépendance de l'effet Zénon sur les caractéristiques des impulsions de mesure[41].

L'interprétation des expériences en termes d'« effet Zénon » permet de décrire l'origine d'un phénomène. Néanmoins, une telle interprétation n'apporte principalement pas de nouveautés non décrites avec l'⁣équation de Schrödinger du système quantique[42],[43].

Plus encore, la description détaillée des expériences avec "l'effet Zénon", en particulier à la limite de la fréquence élevée des mesures (haute efficacité de suppression de transition, ou haute réflectivité d'un miroir strié) ne se comporte généralement pas comme prévu pour une mesure idéalisée[44].

Il a été montré que l'effet quantique Zénon persiste dans les interprétations à plusieurs mondes et à états relatifs de la mécanique quantique[45].

Voir également

 

Références
  1. Sudarshan et Misra, « The Zeno's paradox in quantum theory », Journal of Mathematical Physics, vol. 18, no 4,‎ , p. 756–763 (DOI 10.1063/1.523304, Bibcode 1977JMP....18..756M)
  2. https://phys.org/news/2015-10-zeno-effect-verifiedatoms-wont.html.
  3. Nakanishi, Yamane et Kitano, « Absorption-free optical control of spin systems: the quantum Zeno effect in optical pumping », Physical Review A, vol. 65, no 1,‎ , p. 013404 (DOI 10.1103/PhysRevA.65.013404, Bibcode 2002PhRvA..65a3404N, arXiv quant-ph/0103034)
  4. Facchi, Lidar et Pascazio, « Unification of dynamical decoupling and the quantum Zeno effect », Physical Review A, vol. 69, no 3,‎ , p. 032314 (DOI 10.1103/PhysRevA.69.032314, Bibcode 2004PhRvA..69c2314F, arXiv quant-ph/0303132)
  5. Degasperis, Fonda et Ghirardi, « Does the lifetime of an unstable system depend on the measuring apparatus? », Il Nuovo Cimento A, vol. 21, no 3,‎ , p. 471–484 (DOI 10.1007/BF02731351, Bibcode 1974NCimA..21..471D)
  6. D. Hofstadter, Alan Turing: Life and Legacy of a Great Thinker, Springer, (ISBN 978-3-540-20020-8, lire en ligne), p. 54
  7. Sudarshan et Misra, « The Zeno's paradox in quantum theory », Journal of Mathematical Physics, vol. 18, no 4,‎ , p. 756–763 (DOI 10.1063/1.523304, Bibcode 1977JMP....18..756M)
  8. G. Greenstein et A. Zajonc, The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics, Jones & Bartlett Publishers, (ISBN 978-0-7637-2470-2, lire en ligne), p. 237
  9. Facchi et Pascazio, « Quantum Zeno subspaces », Physical Review Letters, vol. 89, no 8,‎ , p. 080401 (PMID 12190448, DOI 10.1103/PhysRevLett.89.080401, Bibcode 2002PhRvL..89h0401F, arXiv quant-ph/0201115)
  10. Ghirardi, Omero, Rimini et Weber, « Small Time Behaviour of Quantum Nondecay Probability and Zeno's Paradox in Quantum Mechanics », Il Nuovo Cimento A, vol. 52, no 4,‎ , p. 421 (DOI 10.1007/BF02770851, Bibcode 1979NCimA..52..421G)
  11. (en) Kraus, « Measuring processes in quantum mechanics I. Continuous observation and the watchdog effect », Foundations of Physics, vol. 11, nos 7–8,‎ , p. 547–576 (ISSN 0015-9018, DOI 10.1007/bf00726936, Bibcode 1981FoPh...11..547K)
  12. Belavkin et Staszewski, « Nondemolition observation of a free quantum particle », Phys. Rev. A, vol. 45, no 3,‎ , p. 1347–1356 (PMID 9907114, DOI 10.1103/PhysRevA.45.1347, Bibcode 1992PhRvA..45.1347B, arXiv quant-ph/0512138)
  13. P. Ghose, Testing Quantum Mechanics on New Ground, Cambridge University Press, (ISBN 978-0-521-02659-8, lire en ligne), p. 114
  14. G. Auletta, Foundations and Interpretation of Quantum Mechanics, World Scientific, (ISBN 978-981-02-4614-3, lire en ligne), p. 341
  15. Khalfin, « Contribution to the decay theory of a quasi-stationary state », Soviet Physics JETP, vol. 6,‎ , p. 1053 (Bibcode 1958JETP....6.1053K).
  16. Raizen, Wilkinson, Bharucha et Fischer, « Experimental evidence for non-exponential decay in quantum tunnelling », Nature, vol. 387, no 6633,‎ , p. 575 (DOI 10.1038/42418, Bibcode 1997Natur.387..575W, lire en ligne [archive du ]).
  17. (en) Chaudhry, « A general framework for the Quantum Zeno and anti-Zeno effects », Scientific Reports, vol. 6, no 1,‎ , p. 29497 (ISSN 2045-2322, PMID 27405268, PMCID 4942788, DOI 10.1038/srep29497, Bibcode 2016NatSR...629497C, arXiv 1604.06561).
  18. Kouznetsov, Oberst, Neumann et Kuznetsova, « Ridged atomic mirrors and atomic nanoscope », Journal of Physics B, vol. 39, no 7,‎ , p. 1605–1623 (DOI 10.1088/0953-4075/39/7/005, Bibcode 2006JPhB...39.1605K).
  19. Allcock, « The time of arrival in quantum mechanics I. Formal considerations », Annals of Physics, vol. 53, no 2,‎ , p. 253–285 (DOI 10.1016/0003-4916(69)90251-6, Bibcode 1969AnPhy..53..253A).
  20. Echanobe, Del Campo et Muga, « Disclosing hidden information in the quantum Zeno effect: Pulsed measurement of the quantum time of arrival », Physical Review A, vol. 77, no 3,‎ , p. 032112 (DOI 10.1103/PhysRevA.77.032112, Bibcode 2008PhRvA..77c2112E, arXiv 0712.0670).
  21. J. Stolze et D. Suter, Quantum computing: a short course from theory to experiment, Wiley-VCH, (ISBN 978-3-527-40787-3, lire en ligne), p. 99.
  22. « Quantum computer solves problem, without running », Phys.org, (consulté le ).
  23. Franson, Jacobs et Pittman, « Quantum computing using single photons and the Zeno effect », Physical Review A, vol. 70, no 6,‎ , p. 062302 (DOI 10.1103/PhysRevA.70.062302, Bibcode 2004PhRvA..70f2302F, arXiv quant-ph/0408097).
  24. J. von Neumann, Mathematische Grundlagen der Quantenmechanik, Springer, (ISBN 978-3-540-59207-5), Chapter V.2 See also J. von Neumann, Mathematical Foundations of Quantum Mechanics, Princeton University Press, (ISBN 978-0-691-02893-4, lire en ligne), 366); M. B. Menskey, Quantum Measurements and Decoherence, Springer, (ISBN 978-0-7923-6227-2, lire en ligne), §4.1.1, pp. 315 ff; C. Wunderlich et C. Balzer, Quantum Measurements and New Concepts for Experiments with Trapped Ions, vol. 49, Academic Press, coll. « Advances in Atomic, Molecular, and Optical Physics », , 315 p. (ISBN 978-0-12-003849-7, lire en ligne).
  25. Orly Alter and Yoshihisa Yamamoto, « Quantum Zeno Effect and the Impossibility of Determining the Quantum State of a Single System », Phys. Rev. A, vol. 55, no 5,‎ , R2499–R2502 (DOI 10.1103/PhysRevA.55.R2499, Bibcode 1997PhRvA..55.2499A).
  26. Orly Alter and Yoshihisa Yamamoto, Quantum Interferometry, Wiley-VCH, , 539–544 p., « The quantum Zeno effect of a single system is equivalent to the indetermination of the quantum state of a single system ».
  27. Orly Alter and Yoshihisa Yamamoto, Quantum Measurement of a Single System, Wiley-Interscience, (ISBN 9780471283089, DOI 10.1002/9783527617128, lire en ligne).
  28. Mielnik, « The screen problem », Foundations of Physics, vol. 24, no 8,‎ , p. 1113–1129 (DOI 10.1007/BF02057859, Bibcode 1994FoPh...24.1113M)
  29. Yamane, Ito et Kitano, « Quantum Zeno effect in optical fibers », Optics Communications, vol. 192, nos 3–6,‎ , p. 299–307 (DOI 10.1016/S0030-4018(01)01192-0, Bibcode 2001OptCo.192..299Y)
  30. Thun, Peřina et Křepelka, « Quantum Zeno effect in Raman scattering », Physics Letters A, vol. 299, no 1,‎ , p. 19–30 (DOI 10.1016/S0375-9601(02)00629-1, Bibcode 2002PhLA..299...19T)
  31. Peřina, « Quantum Zeno effect in cascaded parametric down-conversion with losses », Physics Letters A, vol. 325, no 1,‎ , p. 16–20 (DOI 10.1016/j.physleta.2004.03.026, Bibcode 2004PhLA..325...16P)
  32. Kouznetsov et Oberst, « Reflection of Waves from a Ridged Surface and the Zeno Effect », Optical Review, vol. 12, no 5,‎ , p. 1605–1623 (DOI 10.1007/s10043-005-0363-9, Bibcode 2005OptRv..12..363K)
  33. Panov, « Quantum Zeno effect in spontaneous decay with distant detector », Physics Letters A, vol. 281, no 1,‎ , p. 9 (DOI 10.1016/S0375-9601(01)00094-9, Bibcode 2001PhLA..281....9P, arXiv quant-ph/0101031)
  34. Itano, Heinzen, Bollinger et Wineland, « Quantum Zeno effect », Physical Review A, vol. 41, no 5,‎ , p. 2295–2300 (PMID 9903355, DOI 10.1103/PhysRevA.41.2295, Bibcode 1990PhRvA..41.2295I, lire en ligne [archive du ])
  35. Leibfried, Blatt, Monroe et Wineland, « Quantum dynamics of single trapped ions », Reviews of Modern Physics, vol. 75, no 1,‎ , p. 281–324 (DOI 10.1103/RevModPhys.75.281, Bibcode 2003RvMP...75..281L)
  36. Fischer, Gutiérrez-Medina et Raizen, « Observation of the Quantum Zeno and Anti-Zeno Effects in an Unstable System », Physical Review Letters, vol. 87, no 4,‎ , p. 040402 (PMID 11461604, DOI 10.1103/PhysRevLett.87.040402, Bibcode 2001PhRvL..87d0402F, arXiv quant-ph/0104035)
  37. Sudarshan et Misra, « The Zeno's paradox in quantum theory », Journal of Mathematical Physics, vol. 18, no 4,‎ , p. 756–763 (DOI 10.1063/1.523304, Bibcode 1977JMP....18..756M)
  38. Patil, Chakram et Vengalattore, « Measurement-Induced Localization of an Ultracold Lattice Gas », Physical Review Letters, vol. 115, no 14,‎ , p. 140402 (ISSN 0031-9007, PMID 26551797, DOI 10.1103/PhysRevLett.115.140402, Bibcode 2015PhRvL.115n0402P, arXiv 1411.2678)
  39. (en) Auteur inconnu « Quantum Zeno Effect Underpinning the Radical-Ion-Pair Mechanism of Avian Magnetoreception », .
  40. Layden, Martin-Martinez et Kempf, « Perfect Zeno-like effect through imperfect measurements at a finite frequency », Physical Review A, vol. 91, no 2,‎ , p. 022106 (DOI 10.1103/PhysRevA.91.022106, Bibcode 2015PhRvA..91b2106L, arXiv 1410.3826)
  41. Streed, Mun, Boyd et Campbell, « Continuous and Pulsed Quantum Zeno Effect », Physical Review Letters, vol. 97, no 26,‎ , p. 260402 (PMID 17280408, DOI 10.1103/PhysRevLett.97.260402, Bibcode 2006PhRvL..97z0402S, arXiv cond-mat/0606430)
  42. Petrosky, Tasaki et Prigogine, « Quantum zeno effect », Physics Letters A, vol. 151, nos 3–4,‎ , p. 109 (DOI 10.1016/0375-9601(90)90173-L, Bibcode 1990PhLA..151..109P)
  43. Petrosky, Tasaki et Prigogine, « Quantum Zeno effect », Physica A, vol. 170, no 2,‎ , p. 306 (DOI 10.1016/0378-4371(91)90048-H, Bibcode 1991PhyA..170..306P)
  44. Kouznetsov, Oberst, Neumann et Kuznetsova, « Ridged atomic mirrors and atomic nanoscope », Journal of Physics B, vol. 39, no 7,‎ , p. 1605–1623 (DOI 10.1088/0953-4075/39/7/005, Bibcode 2006JPhB...39.1605K)
  45. Home et Whitaker, « The many-worlds and relative states interpretations of quantum mechanics, and the quantum Zeno paradox », Journal of Physics A, vol. 20, no 11,‎ , p. 3339–3345 (DOI 10.1088/0305-4470/20/11/036, Bibcode 1987JPhA...20.3339H)

Liens externes
  • Zeno.qcl Un programme informatique écrit en QCL qui démontre l'effet quantique Zénon
  • Portail de la physique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.