Flot (mathématiques)

Dans la suite de l'article, E désigne un espace de Banach. Le symbole (1) désigne l'équation différentielle x' = f(x), où f est fonction définie sur un ouvert Ω de E et à valeurs dans E et (2) l'équation x' = f(t, x). Dans le cas de l'équation (2), Ω désigne un ouvert de R×E et f est toujours une fonction définie sur Ω et à valeurs dans E. La condition de Cauchy appelée C dans l'article, est celle que vérifie une solution s de l'équation. Dans le cas de (1), elle signifie que s(0) = x₀, dans le cas (2) les notations choisies sont : s(t₀) = x₀[Note 1]. Il existe un troisième cas, plus général et qui permet en particulier l'étude des singularités de certaines équations différentielles. L'équation (3) est : x' = f(t, λ, x). Dans ce cas, Ω est un ouvert de R×F×E, où F est encore un espace de Banach. Dans les trois cas, la fonction f est supposée au moins continue, et localement lipschitzienne par rapport à x.

Le flot permet de formaliser un vocabulaire adapté pour l'étude de deux questions concernant les équations différentielles : la sensibilité à la condition initiale et le comportement asymptotique. Ces questions sont au cœur d'une branche mathématique appelée système dynamique.

Si la condition initiale, dite condition de Cauchy, est un peu modifiée, il se peut que la solution de l'équation soit de plus en plus éloignée de la courbe intégrale originelle, si la variable t augmente. Tel est le cas, par exemple, pour les systèmes chaotiques. L'étude de la régularité du flot apporte des premiers éléments de réponse.

Dans certaines conditions et pour une condition initiale donnée, la solution se prolonge à l'infini et « se stabilise » plus ou moins. Elle peut converger vers une valeur, s'approcher de plus en plus d'un comportement périodique, diverger ou encore adopter un comportement différent et appelé chaotique. L'étude de ces différents comportements est l'objet de la seconde question.

Pour l'étude de la sensibilité initiale, on étudie les flot locaux ou globaux, qui permettent d'énoncer une version plus forte du théorème de Cauchy-Lipschitz.

L'étude de la sensibilité à la condition initiale impose un vocabulaire et une représentation géométrique un peu différents de ceux utilisés dans les approches plus élémentaires. Pour en comprendre l'origine de cette différence, le plus simple est de considérer le cas d'une équation différentielle autonome, c'est-à-dire de type (1), d'imaginer que Ω est un plan d'eau et que R représente le temps. le plan d'eau est agité par un courant, représenté par la fonction f, appelée champ de vecteurs. En dimension 2, on représente ce champ de vecteurs en associant à certains points x de Ω une représentation graphique du vecteur f(x), à l'image de la figure de droite. Une courbe intégrale satisfaisant à la condition de Cauchy C peut s'imaginer comme la trajectoire d'un bouchon placé dans l'eau à l'instant initial 0 et à la position x₀. Pour connaître d'un seul coup toutes les solutions de l'équation différentielle, il suffit de connaître le mouvement de la surface de l'eau, appelé flot, coulée ou encore courant[1]. Dans le cas général de l'équation (2), c'est-à-dire celui où l'équation n'est pas nécessairement autonome, on dispose de la définition suivante :

Soit U un voisinage de x₀ tel que {t₀}×U soit inclus dans Ω et J un intervalle ouvert contenant t₀. Un flot local est la donnée d'une application β_t0 de J×U dans E tel que pour tout x de U, l'application de J dans E, qui à t associe β_t0(t, x) soit une courbe intégrale de condition de Cauchy (t₀, x) (c'est-à-dire que β_t0(t₀, x) = x)[2].

Le théorème de Cauchy-Lipschitz garantit l'existence de courbes intégrales maximales. C'est-à-dire que, pour une condition de Cauchy donnée, il existe un intervalle maximal, une unique solution de l'équation définie sur cet intervalle et vérifiant la condition de Cauchy. Ce résultat permet d'enrichir les définitions associées au flot.

Soit x un point de E et J_x l'intervalle égal au domaine de définition de la solution maximale satisfaisant la condition de Cauchy (t₀, x), qui peut être vide si, par exemple, (t₀, x) n'est pas élément de Ω. On note D(f) et on appelle domaine de définition du flot global l'ensemble des couples (t, x) de R×E tel que t soit un élément de J_x^{[réf. nécessaire]}.

Le flot global de f est l'application α_t0^{[réf. à confirmer]} de D(f) dans E, telle que l'application qui à t associe α_t0(t, x) soit la solution maximale de (2) associée à la condition de Cauchy (t₀, x)[3].

Dans toute la suite de l'article α désigne le flot global du champ vectoriel f. Si α ne comporte pas d'indice, cela signifie que la fonction qui à t associe α(t, x) est la courbe intégrale maximale s vérifiant la condition de Cauchy : s(0) = x. Sinon, α_t0 désigne le flot global vérifiant α_t0(t₀, x) = x.

La deuxième question concerne le comportement asymptotique[4] du flot, autrement dit ce qui se passe une fois le système stabilisé, si jamais il se stabilise. Pour la traiter, un vocabulaire spécifique existe ; il suppose en général que l'équation différentielle considérée est autonome[Note 2], c'est-à-dire de type (1) (voir supra).

L'orbite[5] ou la trajectoire d'un point x de Ω est l'image d'une courbe intégrale maximale passant par x.

Le théorème de Cauchy-Lipschitz montre que les orbites forment une partition de Ω.

Un ensemble invariant par le flot[5] est une réunion d'orbites.

Pour reprendre la métaphore de l'introduction, un ensemble A est invariant par le flot si un bouchon qui est dans A y a toujours été et y restera toujours. « Pour les systèmes dynamiques, les parties invariantes jouent le même rôle que les connexes en topologie élémentaire[6] » : on peut limiter l'étude du comportement asymptotique à une telle zone.

Un point de x de Ω est dit point d'équilibre, point fixe ou point stationnaire[5] si son orbite est réduite au singleton {x} ou encore si x est un zéro de la fonction f. S'il existe un voisinage de x tel que toute courbe intégrale maximale qui rencontre ce voisinage converge vers x, le point est dit attractif.

Un point d'équilibre x_e est un point sans courant, ou encore un point tel que, si l'on y place le bouchon, il reste indéfiniment immobile. Deux comportements différents peuvent se produire, le point peut être attractif ou non. Il peut exister une zone pas trop petite (d'intérieur non vide) tel que tout point dans cette zone finit par s'immobiliser en x_e. Ce point semble « attirer » les trajectoires vers lui, pour cette raison, on parle de point attractif. Sinon, tout point se rapprochant de x_e finit par s'éloigner, ce point d'équilibre est alors instable et il faut positionner le bouchon exactement sur le point pour qu'il y reste immobile. Dans le cas général, d'autres comportements que la convergence sont possibles :

Soit s une courbe intégrale définie sur R.

• Lorsque s admet une limite en +∞ et en –∞, l'orbite est dite hétérocline si les deux limites sont distinctes et homocline sinon.
• Si s est périodique, l'orbite est dite périodique.
• L'ensemble ω-limite[6] de l'orbite est l'ensemble des valeurs d'adhérence de la fonction s en +∞. On le note ω(x), où x est un point quelconque de l'orbite. On définit de même l'ensemble α-limite α(x) comme l'ensemble des valeurs d'adhérence de s en –∞.

Ces deux ensembles sont invariants par le flot. Si l'orbite est périodique, ses deux ensembles limites lui sont égaux.

Une notion connexe est celle d'attracteur. L'attracteur futur est le plus petit ensemble contenant tous les ensembles ω(x) si x décrit Ω, à l'exception, peut-être d'un ensemble de mesure nulle. L'attracteur passé correspond à la même définition, mais cette fois-ci avec les ensembles α-limites[4].

Dans sa version élémentaire, le théorème de Cauchy-Lipschitz montre l'existence et l'unicité d'une courbe intégrale maximale. On peut alors définir le flot global α comme la fonction qui, à un triplet (t₁, t₀, x₀) avec (t₀, x₀) élément de Ω, associe (lorsqu'elle est définie) la valeur en t₁ de la solution maximale du problème de Cauchy x' = f(t, x), x(t₀) = x₀. On sait déjà que par rapport à t₁, α est de classe C^p+1 si f est de classe C^p, mais on va préciser son comportement par rapport au triplet (t₁, t₀, x₀) :

• Le flot global est défini sur un ouvert et localement lipschitzien[7].
• Si la fonction f est de classe C^p, il en est de même du flot global[8].

Pour certaines études, comme celles analysant des singularités de courbes intégrales, il est utile d'ajouter un paramètre à l'équation, qui prend la forme : x' = f(t, x, λ). Le flot global dépend alors du paramètre λ, choisi dans un Banach F. La question est celle de la régularité du flot global en fonction du paramètre. Le théorème décrivant cette situation est parfois dénommé « théorème de Cauchy-Lipschitz : cas non autonome avec paramètre[9] ». Si la fonction f est de classe C^p, le flot, considéré comme une application sur un ouvert de R×R×E×F, est aussi de classe C^p.

Dans un premier temps, on étudie le cas de l'équation (2), c'est-à-dire celui d'une équation non nécessairement autonome[10], mais sans paramètre. L'objectif est d'établir la continuité locale d'un flot, c'est-à-dire d'analyser ce qui se passe si la condition de Cauchy est peu modifiée.

On commence par préciser le comportement de α(t, t₀, x₀) par rapport à (t₀, x₀) dans le cas où t est proche de t₀.

En affinant la technique de point fixe utilisée pour démontrer le théorème de Cauchy-Lipschitz classique, on parvient au résultat suivant :

Un flot discontinu ne peut pas se produire si le champ de vecteurs le définissant est continu et défini sur un ouvert.

Pour rendre global le résultat précédent de continuité « au voisinage de la diagonale », il reste encore un peu de travail. Il s'agit surtout de montrer que la configuration de droite ne peut pas se produire. En reprenant la métaphore de l'introduction, on suppose que l'étang contient un rocher. Sur la zone rouge, le flot contourne le rocher, sur la zone bleue il passe tout droit. Le flot possède alors des points de discontinuité. Pour s'en rendre compte, on considère l'évolution d'un voisinage d'un point symbolisé par une zone grise circulaire à un instant 0, sur la figure de droite. Ce point est situé à la frontière des deux zones. À l'instant t₀, ce voisinage est découpé en deux parties éloignées l'une de l'autre. Cette configuration peut se produire, par exemple si Ω n'est pas un ouvert. En revanche, dans les hypothèses étudiées, cette configuration est impossible :

Une remarque est utile pour le démontrer. Elle est formulée ici uniquement pour les équations autonomes[13]. Le point β(s, x) désigne la position, à l'instant s, du point qui était en x à l'instant 0. Le point β(t, β(s, x)) désigne la position à l'instant t, du point qui était en β(s, x), à l'instant 0. Il désigne aussi la position à l'instant s + t du point qui était en position x à l'instant s. Ce qui signifie, si les différentes valeurs sont dans les bons domaines de définitions :

${\displaystyle \beta (t,\beta (s,x))=\beta (t+s,x)\;}$

Ainsi, si les domaines de définitions s'y prêtent, il est possible de combiner les flots locaux, pour en construire un plus vaste. Cette technique permet de munir les flots locaux d'une structure de semi-groupe. Si le flot global est toujours défini sur R, les solutions intégrales maximales partageant une portion de domaine de définition forment un groupe, image de R par un morphisme de groupes.

On souhaite maintenant étudier le cas d'un flot local associé à l'équation :

${\displaystyle (3)\quad {\frac {\mathrm {d} x}{\mathrm {d} t}}=f\left(t,x,\lambda \right)}$.

On suppose que λ est élément d'un espace de Banach F, Ω est un ouvert de R×E×F et f est une fonction continue de Ω dans E, localement lipschitzienne par rapport à (λ, x).

Cette situation, en apparence plus générale que celle de l'équation (2), en est en fait un cas particulier, en remplaçant simplement, dans cette dernière :

• l'espace de Banach E (dans lequel chaque courbe intégrale prend ses valeurs) par E×F ;
• le champ de vecteurs (d'un ouvert de R×E dans E) par la fonction :${\displaystyle g:\Omega \to E\times F,\quad y=\left(t,x,\lambda \right)\mapsto (f(y),0)}$ ;
• l'équation x' = f(t, x) par (x', λ') = g(t, x, λ) ;
• la « condition initiale » (t₀, x₀) par (t₀, x₀, λ₀).

Le flot α dépend maintenant de trois variables : t, t₀, x₀ et la « variable » supplémentaire λ, mais compte tenu de la définition de g, la valeur de λ le long d'une courbe intégrale reste constamment égale à sa valeur initiale λ₀. Cet artifice permet d'étendre directement aux équations à paramètres le résultat du paragraphe précédent : soit f une fonction continue, d'un ouvert de R×F×E dans E, localement lipschitzienne par rapport à ses variables dans F×E. Le flot global associé à l'équation (3) est défini sur un ouvert de R×R×F×E et localement lipschitzien[14].

Mais ce corollaire n'est d'aucune utilité pour la suite, contrairement au théorème suivant, qui généralise le lemme du paragraphe précédent et se démontre (directement) de la même manière :

Le jeu d'écriture lui-même sera utile en revanche, pour étendre aux équations de type (3) un lemme (ci-dessous) sur la régularité C¹.

Les démonstrations associées à la régularité du flot ont pendant longtemps été un peu complexes. De manière indépendante, Pugh^{[réf. souhaitée]} et Robbin[15]^,[16]^,[Note 3] ont trouvé une démonstration élémentaire utilisant le théorème des fonctions implicites. Cette fois, l'équation considérée est celle notée (1), c'est-à-dire qu'on ne traite que d'une équation différentielle autonome. On en déduit une partie du résultat analogue pour les équations non autonomes.

Soient x₀ un point de Ω et b un réel strictement positif tel que la courbe intégrale β₀ qui vaut x₀ en 0 soit définie au moins sur [–b, b]. Choisissons un ouvert Ω' contenant x₀ et un ouvert Ω" contenant Im(β₀) – x₀, tels que Ω' + Ω" soit inclus dans Ω. Notons enfin G l'espace de Banach des fonctions de classe C¹ de [–b, b] dans E et nulles en 0, muni de la norme de la convergence uniforme de la dérivée, V l'ouvert de celles à valeurs dans Ω"[Note 4], et H l'espace de Banach des fonctions continues de [–b, b] dans E, muni de la norme de la convergence uniforme.

On considère l'application T de Ω'×V dans H définie par :

${\displaystyle \forall x\in \Omega '\quad \forall \sigma \in V\quad \forall t\in [-b,b]\quad T(x,\sigma )(t)=\sigma '(t)-f(x+\sigma (t))}$.

Dire qu'un couple (x, σ) est un zéro de la fonction T revient à dire que x + σ est une solution sur [–b, b] de l'équation (1) avec la condition de Cauchy x + σ(0) = x. En particulier, (x₀, β₀ – x₀) est un zéro de T.

On démontre que si f est de classe C¹ alors T aussi et pour b suffisamment petit, T satisfait les hypothèses du théorème des fonctions implicites au point (x₀, β₀ – x₀). Cela signifie que la fonction implicite donnée par l'équation T(x, σ) = 0 est de classe C¹ au voisinage de x₀. Or cette fonction est celle qui associe à x la fonction β(∙, x) – x définie sur [–b, b], ce qui permet de démontrer un premier résultat[17] :

Ce lemme s'étend aux équations différentielles de type (3), par le jeu d'écriture ci-dessus pour le paramètre et un autre, analogue, pour la variable temporelle.

Or dès que f est de classe C¹, la deuxième différentielle partielle de β vérifie une équation différentielle de type (3) :

${\displaystyle D_{1}D_{2}\beta \left(t,x\right)=D_{2}f\left(t,\beta \left(t,x\right)\right)\circ D_{2}\beta \left(t,x\right)}$[18].

Ceci permet de montrer par récurrence que pour toute équation de type (3), si f est de classe C^p alors le flot α(t, t₀, λ, x₀) l'est aussi, par rapport à (t, λ, x₀). Nous admettrons la régularité par rapport à t₀[19], qui utilise entre autres, pour l'initialisation de la récurrence, le théorème de continuité ci-dessus. Moyennant quoi, on peut énoncer :

Le théorème de Cauchy-Lipschitz, sous sa forme élémentaire, garantit à la fois l'existence et l'unicité du flot global α, et sa régularité par rapport à la première variable. Le paragraphe précédent apporte aussi des informations. Il établit que si t est proche de 0 et si t et x varient peu, le flot est de classe C^p, si f l'est. En revanche, la régularité globale du flot α suppose aussi que l'expression α(t, x) soit de classe C^p en x, même si t n'est pas proche de 0. On a supposé ici que (t, x) est un point du domaine de définition de α.

La même technique que dans le paragraphe « Continuité du flot » (voir supra) permet de rendre global le résultat précédent de régularité du flot « au voisinage de la diagonale » pour une équation de type (2) — donc aussi, par le « jeu d'écriture » (voir supra), pour une équation de type (3) :

• Théorème : Pour une équation différentielle non autonome à paramètre, si le champ de vecteurs f est de classe C^p, le flot global l'est aussi[20].

L'équation différentielle x' = –x² n'admet pas de solution sur R tout entier si l'image de 0 n'est pas nulle.

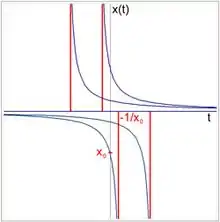
Pour une valeur de x prise dans E, la courbe intégrale maximale t ↦ s(t) = α_t0(t, x) est définie sur un intervalle ouvert. Cet intervalle n'est pas toujours égal à R. Deux « obstacles » peuvent se présenter. Un premier cas est celui où la courbe a pour extrémité un point frontière de l'ouvert Ω. Si tel n'est pas le cas, il n'existe qu'un seul obstacle possible : la dérivée de s n'est pas bornée. Cela résulte de la proposition suivante[21] :

• Soit b la borne supérieure du domaine de définition d'une courbe intégrale maximale s. Si b est fini et si s' est bornée au voisinage de b, alors s admet au point b une limite c et le couple (b, c) appartient à la frontière de Ω.

Un exemple[22]^,[Note 5] est donné par l'équation x' = –x². La solution s'écrit :

${\displaystyle \alpha (t,x)={\frac {x}{xt+1}}}$.

Les courbes intégrales dont l'ordonnée à l'origine est différente de 0 ne se prolongent pas au-delà de –1/x.

Le système dynamique de Lorenz montre un exemple où les ensembles ω-limites sont en général de structure complexe.

On suppose ici que l'équation différentielle étudiée est autonome. Une méthode pour étudier le comportement asymptotique est d'analyser l'ensemble ω-limite d'une orbite. Cet ensemble possède toujours les propriétés suivantes :

• Soit x un élément de Ω, l'ensemble ω-limite ω(x) est un fermé invariant par le flot.

En particulier, si y est un point de la trajectoire passant par x, alors ω(x) = ω(y). Si l'orbite de x n'est pas à valeurs dans un ensemble borné, la proposition peut s'avérer moins forte qu'il n'y parait : l'ensemble ω(x) peut être vide. Tel est le cas si la courbe intégrale s ayant pour condition de Cauchy s(0) = x est définie par s(t) = tv où v est un vecteur non nul de E. Si l'orbite est compacte, on a par contre :

• Avec les notations précédentes, si la trajectoire de x est à valeurs dans un compact K, ω(x) est un connexe compact non vide[23].

La trajectoire peut néanmoins être complexe, le système dynamique de Lorenz est un exemple exhibant des ensembles ω-limites compacts dont la dimension de Hausdorff n'est pas égale à 1.

Il existe un cas où le flot dispose d'un comportement asymptotique relativement simple, il se produit si l'équation différentielle associée est autonome, si l'espace E est le plan et si la courbe intégrale considérée est compacte. On dispose alors du théorème suivant, si α est le flot et x un point de Ω.

• Dans le cadre des hypothèses du paragraphe, la fonction qui à t associe α(t, x) est définie sur R. Si cette fonction n'est pas convergente, l'ensemble ω-limite est l'image d'une orbite cyclique[24].

Ce théorème se généralise mal. Si E est de dimension strictement supérieure à 2, le système dynamique de Lorenz montre que le résultat du théorème n'est plus généralement vrai.

• Marcel Berger et Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions]
  Ce livre se limite au cas où E est un espace vectoriel de dimension finie. Il traite presque de l'intégralité des informations de l'article sur la sensibilité à la condition initiale, à l'exception du caractère C^p du flot local.
• Serge Cantat, « Théorème de Poincaré-Bendixson », Le journal de maths des élèves, ENS Lyon, vol. 1, n^o 3,‎ 1995 (lire en ligne)
• (en) Serge Lang, Real and Functional Analysis, coll. « GTM » (n^o 142), 1993, 3^e éd., 580 p. (lire en ligne)
• Paul Malliavin, Géométrie différentielle intrinsèque, Hermann, 1972 (ISBN 2-7056-5696-0)
  Cette référence, encore sur la sensibilité à la condition initiale, est plus complète, mais plus ardue que la précédente. L'orientation est définitivement géométrique.
• Daniel Leborgne, Calcul différentiel et géométrie, Paris, PUF, 1982, 262 p. (ISBN 2-13-037495-6)
  Ce livre suppose déjà connu le théorème dans le cas des Banach et le généralise aux variétés différentielles. Il ne traite pas l'analyse du comportement asymptotique d'un flot.
• Frédéric Paulin, « Topologie, analyse et calcul différentiel », École Normale Supérieure, 2008
• Tewfik Sari, « Introduction aux systèmes dynamiques et applications à un modèle cosmologique », sur Université de Haute-Alsace, 2006, publié dans Géométries et dynamiques, Hermann, 2008 (ISBN 978-2-70566772-6), p. 259-274