Fonction de Wigner

Une particule classique a une position et une quantité de mouvement définies et est donc représentée par un point dans l'espace des phases. Étant donné un ensemble de particules, la probabilité de trouver une particule à une certaine position dans l'espace des phases est spécifiée par une distribution de probabilité, la densité de Liouville. Cette interprétation stricte échoue pour une particule quantique, en raison du principe d'incertitude, qui interdit la détermination simultanée de la position et de l'impulsion d'une particule. La distribution de Wigner joue un rôle analogue à la densité de Liouville, mais ne satisfait pas toutes les propriétés d'une distribution de probabilité conventionnelle ; on la qualifie donc de distribution de "quasi-probabilité"; mais inversement, elle a des caractéristiques topologiques que n'a pas une distribution classique.

Par exemple, la distribution de Wigner peut prendre et prend normalement des valeurs négatives pour les états qui n'ont pas d'équivalent classique - c'est une spécificité de la mécanique quantique (voir ci-dessous pour une caractérisation des états purs dont les fonctions de Wigner sont non négatives). Le lissage de la distribution de Wigner via un filtre de taille supérieure à ħ donne une fonction semi-définie positive : par exemple, par la transformée de Weierstrass, qui est une convolution avec une gaussienne dans l'espace des phases (représentation d'Husimi, voir ci-dessous). Cette opération de lissage correspond à une transition vers le régime semi-classique.

On peut prouver que les régions où la distribution de Wigner prend des valeurs négatives sont "petites" (en les convoluant avec une gaussienne de faible largeur) : elles ne peuvent pas s'étendre à des régions compactes supérieures à quelques ħ, et donc disparaissent dans la limite classique. Ces régions à valeur négative sont protégées par le principe d'incertitude, qui ne permet pas une localisation précise dans des régions d'espace de phase inférieures à ħ, et rend ainsi de telles "probabilités négatives" moins paradoxales.

La distribution de Wigner W(x,p) d'un état pur est définie comme

${\displaystyle W(x,p)~{\stackrel {\text{def}}{=}}~{\frac {1}{\pi \hbar }}\int _{-\infty }^{\infty }\psi ^{*}(x+y)\psi (x-y)e^{2ipy/\hbar }\,dy,}$

où ψ est la fonction d'onde définie dans l'espace des positions, et x et p sont la position et l'impulsion, mais pourraient être n'importe quelle paire de variables conjuguées (par exemple parties réelles et imaginaires du champ électrique ou fréquence et temps d'un signal). Notez que W(x,p) peut être non-nulle dans des domaines où la fonction d'onde s'annule ("battements").

On peut la définir symétriquement à partir de la fonction d'onde dans l'espace des moments :

${\displaystyle W(x,p)={\frac {1}{\pi \hbar }}\int _{-\infty }^{\infty }\varphi ^{*}(p+q)\varphi (p-q)e^{-2ixq/\hbar }\,dq,}$

où φ est la fonction d'onde normalisée dans l'espace des moments, proportionnelle à la transformée de Fourier de ψ .

En trois dimensions, elle s'écrit :

${\displaystyle W({\vec {r}},{\vec {p}})={\frac {1}{(2\pi )^{3}}}\int \psi ^{*}({\vec {r}}+\hbar {\vec {s}}/2)\psi ({\vec {r}}-\hbar {\vec {s}}/2)e^{i{\vec {p}}\cdot {\vec {s}}}\,d^{3}s.}$

Dans le cas général, qui inclut des combinaisons d'états purs, c'est la transformée de Wigner de la matrice densité ${\displaystyle {\hat {\rho }}}$ :

${\displaystyle W(x,p)={\frac {1}{\pi \hbar }}\int _{-\infty }^{\infty }\langle x+y|{\hat {\rho }}|x-y\rangle e^{-2ipy/\hbar }\,dy,}$

où ⟨ x | ψ ⟩ = ψ(x) . Cette transformation de Wigner est l'inverse de la transformée de Wigner-Weyl, qui projettent les fonctions de l'espace des phases vers des opérateurs de l'espace de Hilbert (voir l'article en anglais quantification de Weyl .

Ainsi, la fonction de Wigner est-elle la pierre angulaire de la mécanique quantique dans l'espace des phases.

En 1949, José Enrique Moyal a établi comment la fonction de Wigner permet de définir l' espérance mathématique (la mesure) dans l'espace des phases (de manière analogue à celle avec une fonction de densité de probabilité) ; cette mesure produit la valeur moyenne attendue d'observables Ĝ représentées par des fonctions de variables réelles dans l'espace des phases g(x, p) ; les fonctions g(x, p) sont associées de manière unique aux opérateurs Ĝ (convenablement ordonnés) par la transformée de Weyl (voir la quantification de Weyl et la propriété 7 ci-dessous), d'une manière qui évoque la théorie classique des probabilités .

Plus précisément, la valeur moyenne mesurable d'une observable quantique représentée par un opérateur Ĝ est une "moyenne dans l'espace des phases" de la transformée de Wigner de cet opérateur :

${\displaystyle \langle {\hat {G}}\rangle =\int dx\,dp\,W(x,p)g(x,p).}$

La distribution de quasi-probabilité de Wigner pour différents états propres d'énergie de l' oscillateur harmonique quantique : a) n = 0 (état fondamental), b) n = 1, c) n = 5

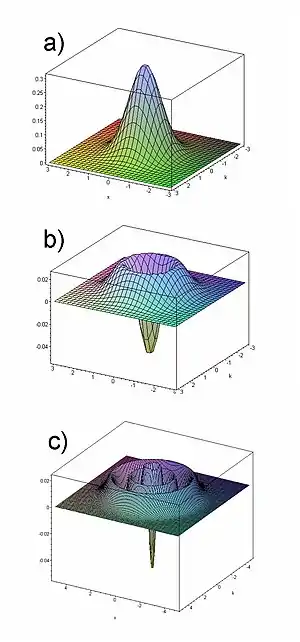
1. W(x,p) est une fonction à valeurs réelles.

2. Les distributions de probabilité x et p sont données par les lois marginales ; en général :

${\displaystyle \int _{-\infty }^{\infty }dp\,W(x,p)=\langle x|{\hat {\rho }}|x\rangle .}$ Si le système peut être décrit par un état pur, on obtient :${\displaystyle \int _{-\infty }^{\infty }dp\,W(x,p)=|\psi (x)|^{2}.}$

${\displaystyle \int _{-\infty }^{\infty }dx\,W(x,p)=\langle p|{\hat {\rho }}|p\rangle .}$ Si le système peut être décrit par un état pur, on a ${\displaystyle \int _{-\infty }^{\infty }dx\,W(x,p)=|\varphi (p)|^{2}.}$

Et :

${\displaystyle \int _{-\infty }^{\infty }dx\int _{-\infty }^{\infty }dp\,W(x,p)=\operatorname {Tr} ({\hat {\rho }}).}$

Typiquement la trace de la matrice densité ${\displaystyle {\hat {\rho }}}$ est égale à 1 ; la fonction W (x,p) est normée à l'unité.

3. W(x,p) a les symétries de réflexion suivantes :

• Symétrie temporelle : ${\displaystyle \psi (x)\to \psi (x)^{*}\Rightarrow W(x,p)\to W(x,-p).}$
• Symétrie spatiale : ${\displaystyle \psi (x)\to \psi (-x)\Rightarrow W(x,p)\to W(-x,-p).}$

4. W(x,p) est compatible avec la transformation de Galilée :

${\displaystyle \psi (x)\to \psi (x+y)\Rightarrow W(x,p)\to W(x+y,p).}$

Elle n'est pas compatible avec la transformation de Lorentz

, et donc pas compatible avec les relativités restreinte et générale

5. L'équation du mouvement pour chaque point de l'espace des phases est classique en l'absence de forces :

${\displaystyle {\frac {\partial W(x,p)}{\partial t}}={\frac {-p}{m}}{\frac {\partial W(x,p)}{\partial x}}.}$

En fait, elle est classique même en présence de potentiels harmoniques.

6. Le recouvrement de 2 états ${\displaystyle {\hat {\psi }}}$ et ${\displaystyle {\hat {\theta }}}$ est calculé comme suit

${\displaystyle |\langle \psi |\theta \rangle |^{2}=2\pi \hbar \int _{-\infty }^{\infty }dx\int _{-\infty }^{\infty }dp\,W_{\psi }(x,p)W_{\theta }(x,p).}$

7. Les valeurs moyennes mesurables d'un opérateur ${\displaystyle {\hat {G}}}$ sont calculées comme des moyennes dans l'espace des phases des transformées de Wigner respectives :

${\displaystyle g(x,p)\equiv \int _{-\infty }^{\infty }dy\,\left\langle x-{\frac {y}{2}}\right|{\hat {G}}\left|x+{\frac {y}{2}}\right\rangle e^{ipy/\hbar },}$

${\displaystyle \langle \psi |{\hat {G}}|\psi \rangle =\operatorname {Tr} ({\hat {\rho }}{\hat {G}})=\int _{-\infty }^{\infty }dx\int _{-\infty }^{\infty }dp\,W(x,p)g(x,p).}$

8. Pour que W(x,p) représente des matrices de densité de systèmes physiques (positives), elle doit satisfaire la relation

${\displaystyle \int _{-\infty }^{\infty }dx\,\int _{-\infty }^{\infty }dp\,W(x,p)W_{\theta }(x,p)\geq 0}$

pour tout état pur |θ⟩.

9. En vertu de l' inégalité de Cauchy-Schwarz, pour un état pur, elle est bornée :

${\displaystyle -{\frac {2}{h}}\leq W(x,p)\leq {\frac {2}{h}}.}$

Cette borne disparaît dans la limite classique, ħ → 0. Dans cette limite, W(x,p) se réduit à la densité de probabilité dans l'espace de coordonnées x, généralement très localisée, multipliée par des fonctions-δ en quantité de mouvement : la limite classique est une structure en forme de «peigne». Aussi, en raison du principe d'incertitude, cette limite de la mécanique quantique exclut une fonction de Wigner qui serait une fonction-δ parfaitement localisée dans l'espace des phases.

10. La transformation de Wigner est simplement la transformée de Fourier des antidiagonales de la matrice de densité, lorsque cette matrice est exprimée dans l'espace des positions[7].

Comme vu précédemment, la transformation de Wigner est une transformation inversible d'un opérateur Ĝ sur un espace de Hilbert en une fonction ${\displaystyle g(x,p)}$ dans l'espace des phases et est donnée par

${\displaystyle g(x,p)=\int _{-\infty }^{\infty }ds\,e^{ips/\hbar }\left\langle x-{\frac {s}{2}}\right|{\hat {G}}\left|x+{\frac {s}{2}}\right\rangle .}$

Les opérateurs hermitiens se transforment en des fonctions réelles. L'inverse de cette transformation, de l'espace des phases à l'espace de Hilbert, s'appelle la transformation de Weyl :  :

${\displaystyle \langle x|{\hat {G}}|y\rangle =\int _{-\infty }^{\infty }{\frac {dp}{h}}e^{ip(x-y)/\hbar }g\left({\frac {x+y}{2}},p\right)}$

(à ne pas confondre avec la transformation de Weyl en géométrie différentielle).

La fonction de Wigner W(x, p) discutée ici est donc considérée comme la transformée de Wigner de l'opérateur de matrice de densité ${\displaystyle {\hat {\rho }}}$. Ainsi, la trace d'un opérateur avec la matrice de densité se transforme en l'intégrale dans l'espace des phases du produit de g(x, p) avec la fonction de Wigner.

L'équation d'évolution de la fonction de Wigner se déduit de l'équation d'évolution de la matrice densité de von Neumann dans la représentation de Schrödinger ; c'est l'équation d'évolution de Moyal pour la fonction de Wigner :

${\displaystyle {\frac {\partial W(x,p,t)}{\partial t}}=-\{\{W(x,p,t),H(x,p)\}\},}$

${\displaystyle H(x,p)}$ est l'hamiltonien du système, et {{⋅, ⋅}} est le crochet de Moyal. De manière plus explicite, en introduisant les dérivées partielles à gauche ${\displaystyle {\overset {_{\gets }}{\partial }}_{x}}$et ${\displaystyle {\vec {\partial }}_{x}}$ à droite, on obtient

${\displaystyle {\frac {\partial W}{\partial t}}=-\{\{W,H\}\}=-{\frac {2}{\hbar }}W\sinh \left({\frac {\hbar }{2}}({\overset {_{\gets }}{\partial }}_{x}{\vec {\partial }}_{p}-{\overset {_{\gets }}{\partial }}_{p}{\vec {\partial }}_{x})\right)H=-\{W,H\}+O(\hbar ^{2}).}$

Dans la limite classique, ħ → 0, le crochet de Moyal se réduit au crochet de Poisson, et l'équation d'évolution se réduit à l'équation de Liouville de la mécanique statistique classique.

Formellement, l'équation classique de Liouville peut être résolue en termes de trajectoires de particules dans l'espace des phases qui sont des solutions des équations classiques de Hamilton. Cette technique de résolution d'équations aux dérivées partielles est connue sous le nom de méthode des caractéristiques. Cette méthode se transpose aux systèmes quantiques, où les "trajectoires" des caractéristiques déterminent désormais l'évolution des fonctions de Wigner. La solution de l'équation d'évolution de Moyal pour la fonction de Wigner est représentée formellement par

${\displaystyle W(x,p,t)=W{\big (}\star {\big (}x_{-t}(x,p),p_{-t}(x,p){\big )},0{\big )},}$

où ${\displaystyle x_{t}(x,p)}$ et ${\displaystyle p_{t}(x,p)}$ sont les trajectoires caractéristiques soumises aux équations quantiques de Hamilton avec des conditions initiales ${\displaystyle x_{t=0}(x,p)=x}$ et ${\displaystyle p_{t=0}(x,p)=p}$, et où le produit-${\displaystyle \star }$ de composition des fonctions est complètement non local (le "fluide de probabilité quantique" diffuse, comme l'a observé Moyal), les traces des trajectoires locales dans les systèmes quantiques sont à peine perceptibles dans l'évolution de la fonction de distribution de Wigner[9]. Dans la représentation intégrale des produits-${\displaystyle \star }$, leurs actions successives ont été adaptées à une intégrale de chemin dans l'espace de phase, pour résoudre l'équation d'évolution de la fonction de Wigner [10] (voir aussi [11]^,[12]^,[13] ). Cette caractéristique non locale de l'évolution temporelle de Moyal [14] est illustrée dans la galerie de figures ci-dessous, pour des hamiltoniens plus complexes que l'oscillateur harmonique. A la limite classique, l'évolution temporelle des fonctions de Wigner ayant l'aspect de trajectoires devient de plus en plus distinct. A ħ = 0, les trajectoires des caractéristiques se réduisent aux trajectoires classiques des particules dans l'espace des phases.

Un tracé de contour de la distribution Wigner – Ville pour une impulsion lumineuse modulée. Le graphique montre clairement que la fréquence est une fonction linéaire du temps.

• Dans la modélisation de systèmes optiques tels que les télescopes ou les dispositifs de télécommunications à fibre, la fonction de Wigner est utilisée pour combler le fossé entre le simple traçage de rayons et l'analyse des ondes complètes du système. Ici p/ħ est remplacé par k = |k| sin θ ≈ |k|θ dans l'approximation aux petits angles. Dans ce contexte, la fonction de Wigner est la plus proche que l'on puisse obtenir pour décrire le système en termes de rayons à la position x et à l'angle θ tout en incluant les effets des interférences [25]. S'il devient négatif à un moment donné, un simple lancer de rayons ne suffira pas à modéliser le système. C'est-à-dire que les valeurs négatives de cette fonction sont un symptôme de la limite de Gabor du signal lumineux classique et non des caractéristiques quantiques de la lumière associées à ħ.
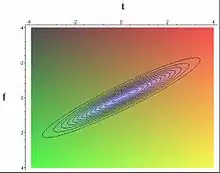
• Dans le traitement du signal, un signal électrique variable dans le temps, une vibration mécanique ou une onde sonore sont représentés par une fonction de Wigner. Ici, x est remplacé par le temps, et p/ħ est remplacé par la fréquence angulaire ω = 2πf, où f est la fréquence habituelle.
• En optique ultrarapide, les impulsions laser courtes sont caractérisées par la fonction de Wigner utilisant les mêmes substitutions f et t que ci-dessus. Les défauts d'impulsion tels que le chirp (le changement de fréquence avec le temps) peuvent être visualisés avec la fonction de Wigner.
• En optique quantique, x et p/ħ sont remplacés par les quadratures X et P, les composantes réelle et imaginaire du champ électrique (voir état cohérent ).

La distribution de Wigner a été la première distribution de quasi-probabilité à être formulée, mais de nombreuses autres ont suivi, formellement équivalentes et transformables les unes dans les autres (voir l'article en anglais Transformation entre distributions dans l'analyse temps-fréquence). Comme dans le cas des systèmes de coordonnées, en raison de leurs propriétés particulières, plusieurs d'entre elles présentent des avantages pour des applications spécifiques :

• Représentation de Glauber P
• Représentation Husimi Q[21]

Néanmoins, la distribution de Wigner occupe une position privilégiée parmi toutes ces distributions, car c'est la seule dont le produit en étoile requis disparait (s'intègre par parties jusqu'à l'unité ) dans l'évaluation des valeurs moyennes, comme illustré ci-dessus, et peut donc être visualisée comme une mesure de quasi-probabilité analogue aux mesures classiques.

Comme indiqué plus haut, la formule de la fonction de Wigner a été dérivée indépendamment plusieurs fois dans différents contextes. En fait, apparemment, Wigner ignorait que même dans le contexte de la théorie quantique, elle avait été introduite précédemment par Heisenberg et Dirac[26], bien que purement formellement : ces deux précurseurs n'ont pas compris sa signification, et celle de ses valeurs négatives, car ils ne la considéraient que comme une approximation de la description quantique complète d'un système tel que l'atome. Symétriquement, dans la plupart de sa correspondance légendaire de 18 mois avec Moyal au milieu des années 1940, Dirac ignorait que la fonction génératrice de moment quantique de Moyal était effectivement la fonction de Wigner, et c'est Moyal qui l'a finalement portée à son attention[27].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Quasiprobability Wigner transform » (voir la liste des auteurs).